Uncovering Causality from Multivariate Hawkes Integrated Cumulants

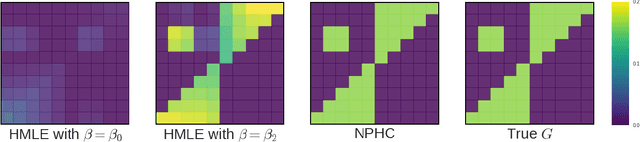
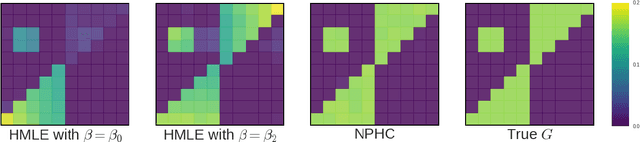
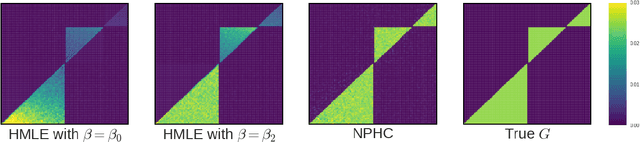
We design a new nonparametric method that allows one to estimate the matrix of integrated kernels of a multivariate Hawkes process. This matrix not only encodes the mutual influences of each nodes of the process, but also disentangles the causality relationships between them. Our approach is the first that leads to an estimation of this matrix without any parametric modeling and estimation of the kernels themselves. A consequence is that it can give an estimation of causality relationships between nodes (or users), based on their activity timestamps (on a social network for instance), without knowing or estimating the shape of the activities lifetime. For that purpose, we introduce a moment matching method that fits the third-order integrated cumulants of the process. We show on numerical experiments that our approach is indeed very robust to the shape of the kernels, and gives appealing results on the MemeTracker database.

SGD with Variance Reduction beyond Empirical Risk Minimization

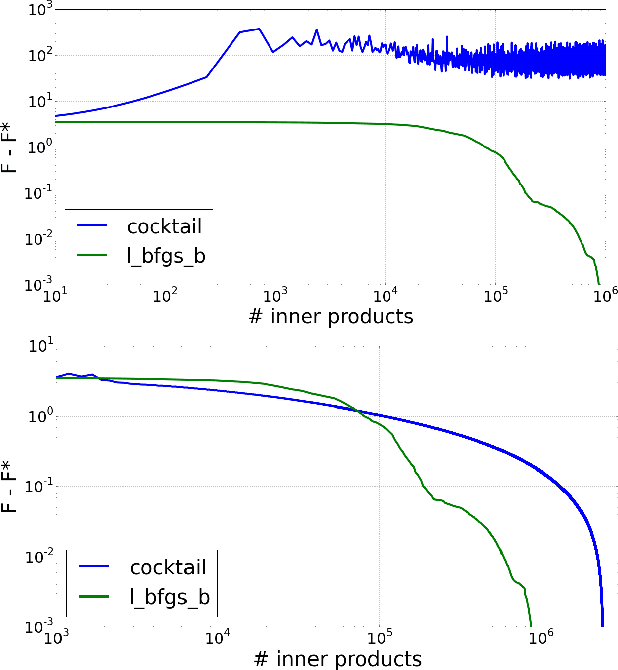
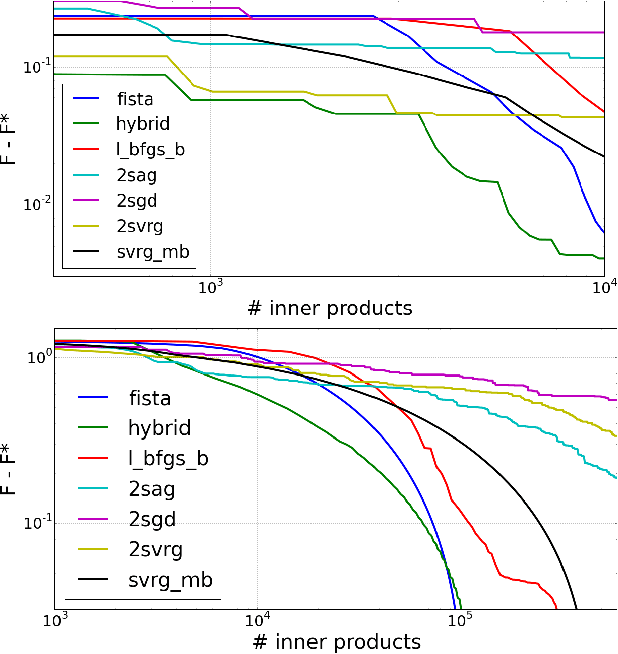
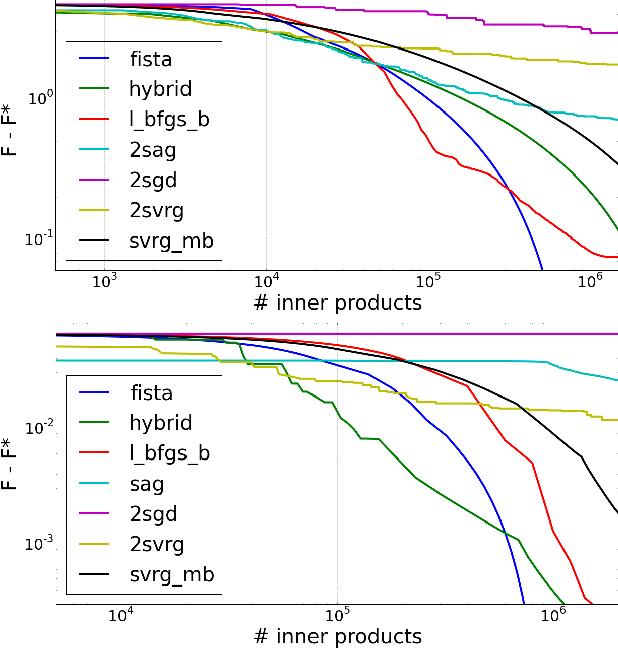
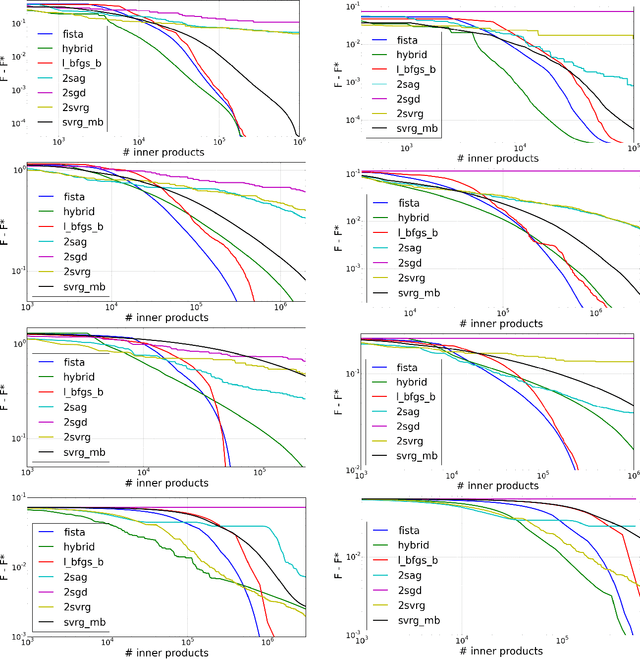
We introduce a doubly stochastic proximal gradient algorithm for optimizing a finite average of smooth convex functions, whose gradients depend on numerically expensive expectations. Our main motivation is the acceleration of the optimization of the regularized Cox partial-likelihood (the core model used in survival analysis), but our algorithm can be used in different settings as well. The proposed algorithm is doubly stochastic in the sense that gradient steps are done using stochastic gradient descent (SGD) with variance reduction, where the inner expectations are approximated by a Monte-Carlo Markov-Chain (MCMC) algorithm. We derive conditions on the MCMC number of iterations guaranteeing convergence, and obtain a linear rate of convergence under strong convexity and a sublinear rate without this assumption. We illustrate the fact that our algorithm improves the state-of-the-art solver for regularized Cox partial-likelihood on several datasets from survival analysis.