SGD with Variance Reduction beyond Empirical Risk Minimization
Paper and Code
Nov 08, 2016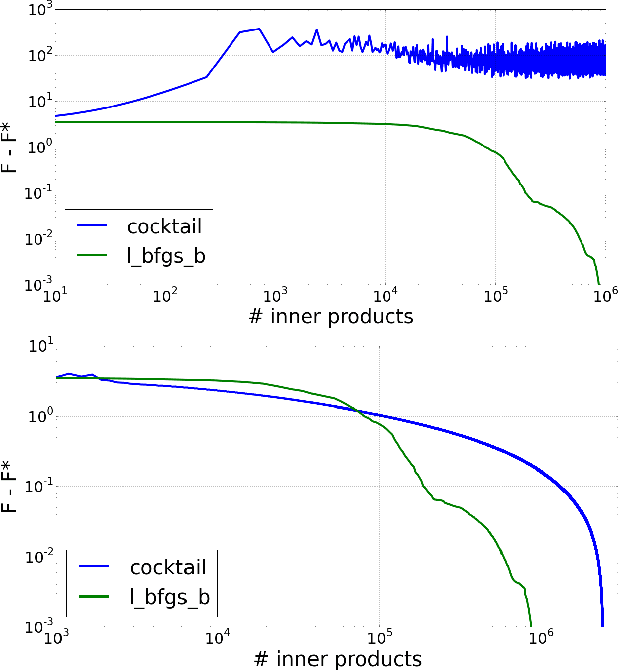
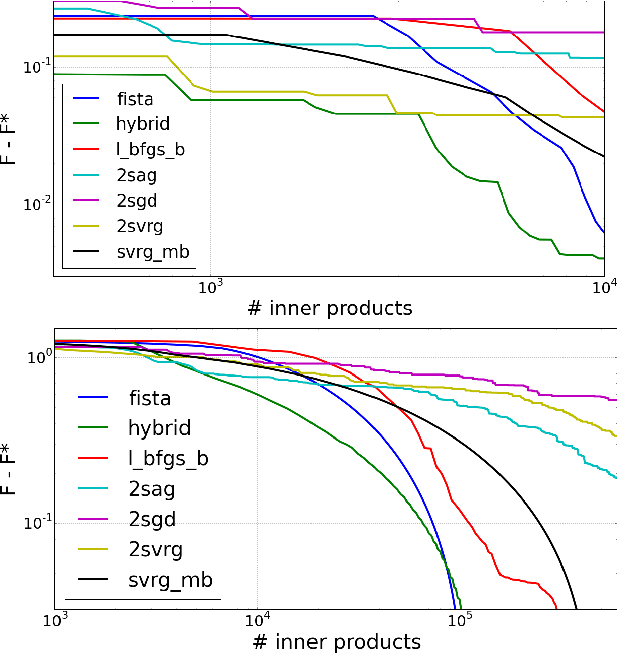
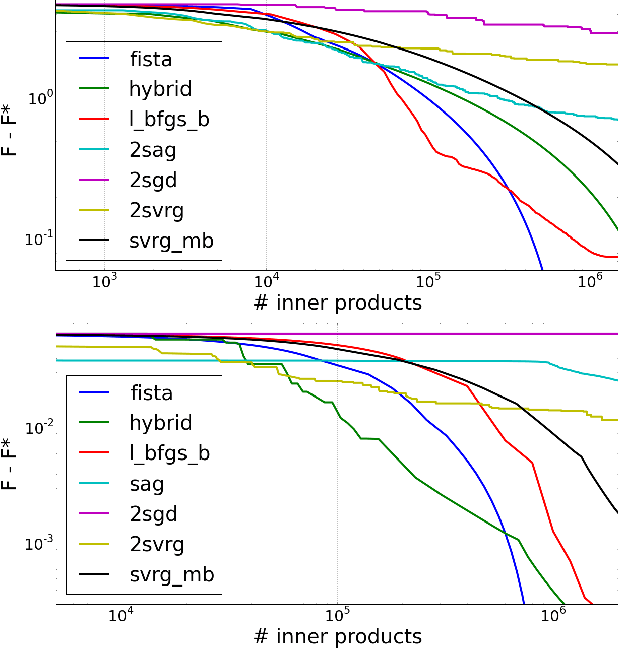
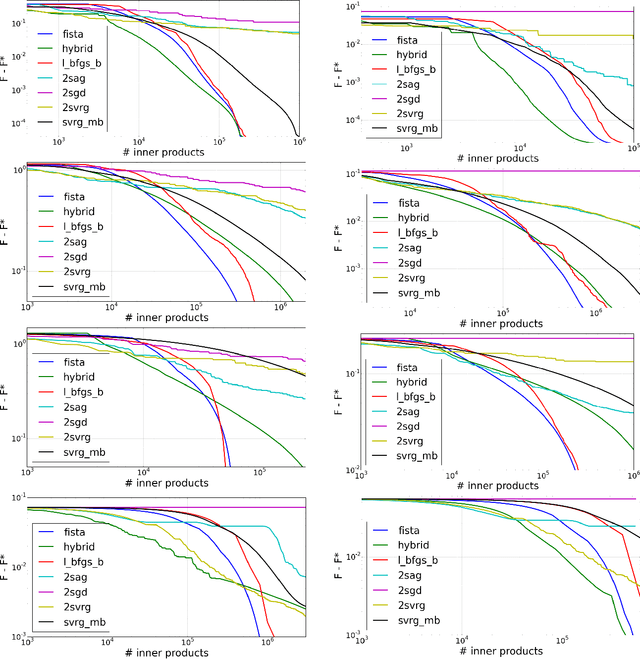
We introduce a doubly stochastic proximal gradient algorithm for optimizing a finite average of smooth convex functions, whose gradients depend on numerically expensive expectations. Our main motivation is the acceleration of the optimization of the regularized Cox partial-likelihood (the core model used in survival analysis), but our algorithm can be used in different settings as well. The proposed algorithm is doubly stochastic in the sense that gradient steps are done using stochastic gradient descent (SGD) with variance reduction, where the inner expectations are approximated by a Monte-Carlo Markov-Chain (MCMC) algorithm. We derive conditions on the MCMC number of iterations guaranteeing convergence, and obtain a linear rate of convergence under strong convexity and a sublinear rate without this assumption. We illustrate the fact that our algorithm improves the state-of-the-art solver for regularized Cox partial-likelihood on several datasets from survival analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge