Exact, Tractable Gauss-Newton Optimization in Deep Reversible Architectures Reveal Poor Generalization

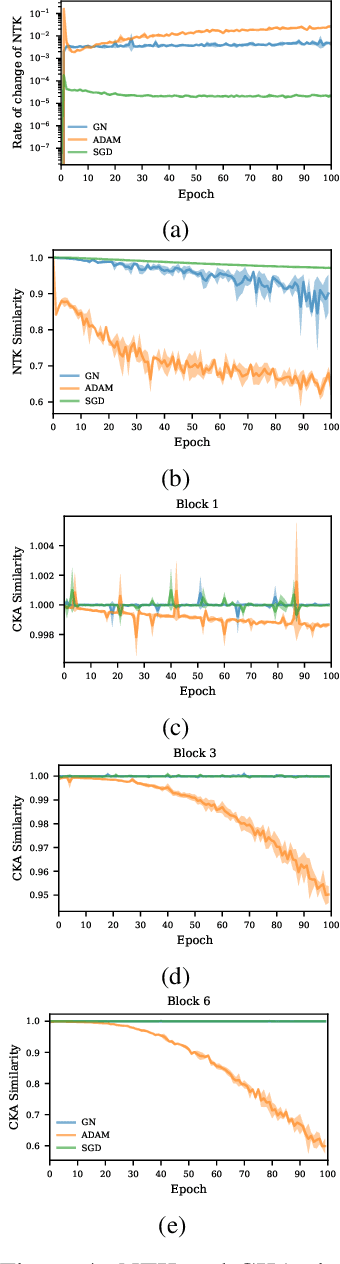
Second-order optimization has been shown to accelerate the training of deep neural networks in many applications, often yielding faster progress per iteration on the training loss compared to first-order optimizers. However, the generalization properties of second-order methods are still being debated. Theoretical investigations have proved difficult to carry out outside the tractable settings of heavily simplified model classes -- thus, the relevance of existing theories to practical deep learning applications remains unclear. Similarly, empirical studies in large-scale models and real datasets are significantly confounded by the necessity to approximate second-order updates in practice. It is often unclear whether the observed generalization behaviour arises specifically from the second-order nature of the parameter updates, or instead reflects the specific structured (e.g.\ Kronecker) approximations used or any damping-based interpolation towards first-order updates. Here, we show for the first time that exact Gauss-Newton (GN) updates take on a tractable form in a class of deep reversible architectures that are sufficiently expressive to be meaningfully applied to common benchmark datasets. We exploit this novel setting to study the training and generalization properties of the GN optimizer. We find that exact GN generalizes poorly. In the mini-batch training setting, this manifests as rapidly saturating progress even on the \emph{training} loss, with parameter updates found to overfit each mini-batchatch without producing the features that would support generalization to other mini-batches. We show that our experiments run in the ``lazy'' regime, in which the neural tangent kernel (NTK) changes very little during the course of training. This behaviour is associated with having no significant changes in neural representations, explaining the lack of generalization.

Sample-efficient Bayesian Optimisation Using Known Invariances

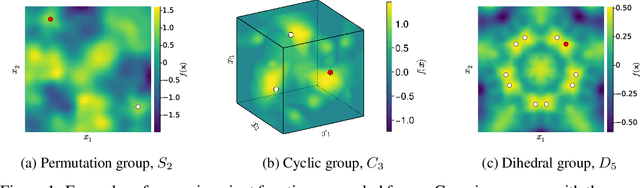
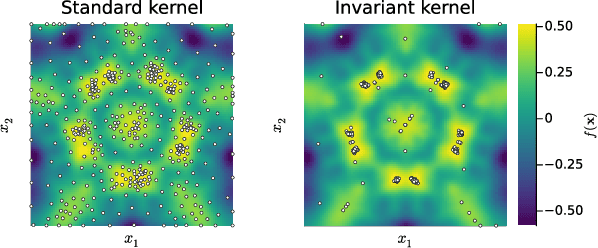
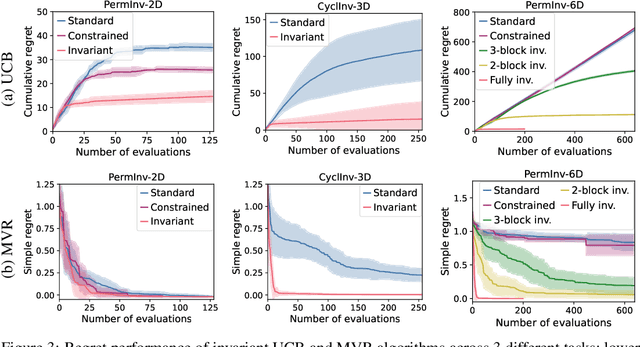
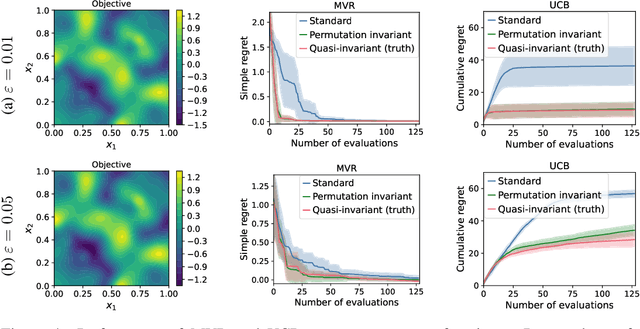
Bayesian optimisation (BO) is a powerful framework for global optimisation of costly functions, using predictions from Gaussian process models (GPs). In this work, we apply BO to functions that exhibit invariance to a known group of transformations. We show that vanilla and constrained BO algorithms are inefficient when optimising such invariant objectives, and provide a method for incorporating group invariances into the kernel of the GP to produce invariance-aware algorithms that achieve significant improvements in sample efficiency. We derive a bound on the maximum information gain of these invariant kernels, and provide novel upper and lower bounds on the number of observations required for invariance-aware BO algorithms to achieve $\epsilon$-optimality. We demonstrate our method's improved performance on a range of synthetic invariant and quasi-invariant functions. We also apply our method in the case where only some of the invariance is incorporated into the kernel, and find that these kernels achieve similar gains in sample efficiency at significantly reduced computational cost. Finally, we use invariant BO to design a current drive system for a nuclear fusion reactor, finding a high-performance solution where non-invariant methods failed.

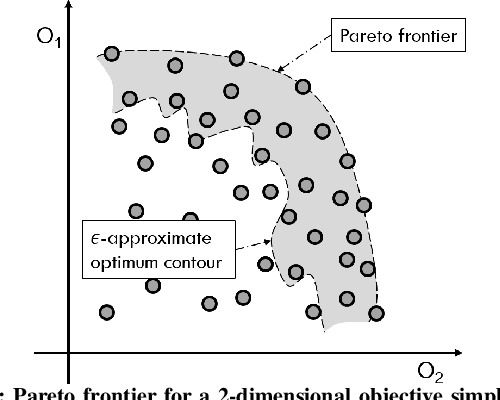
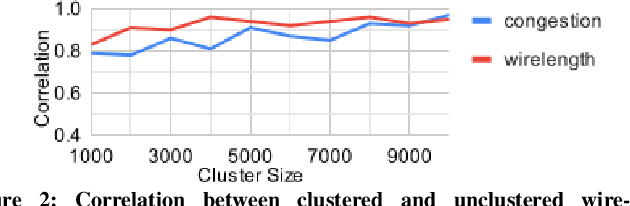
Flexible Multiple-Objective Reinforcement Learning for Chip Placement

Recently, successful applications of reinforcement learning to chip placement have emerged. Pretrained models are necessary to improve efficiency and effectiveness. Currently, the weights of objective metrics (e.g., wirelength, congestion, and timing) are fixed during pretraining. However, fixed-weighed models cannot generate the diversity of placements required for engineers to accommodate changing requirements as they arise. This paper proposes flexible multiple-objective reinforcement learning (MORL) to support objective functions with inference-time variable weights using just a single pretrained model. Our macro placement results show that MORL can generate the Pareto frontier of multiple objectives effectively.

How to distribute data across tasks for meta-learning?

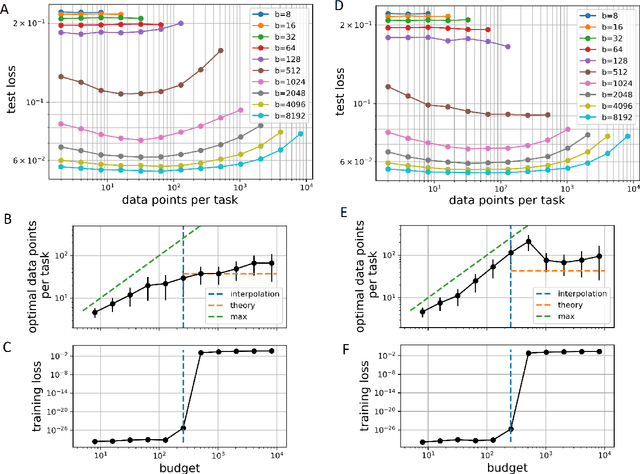
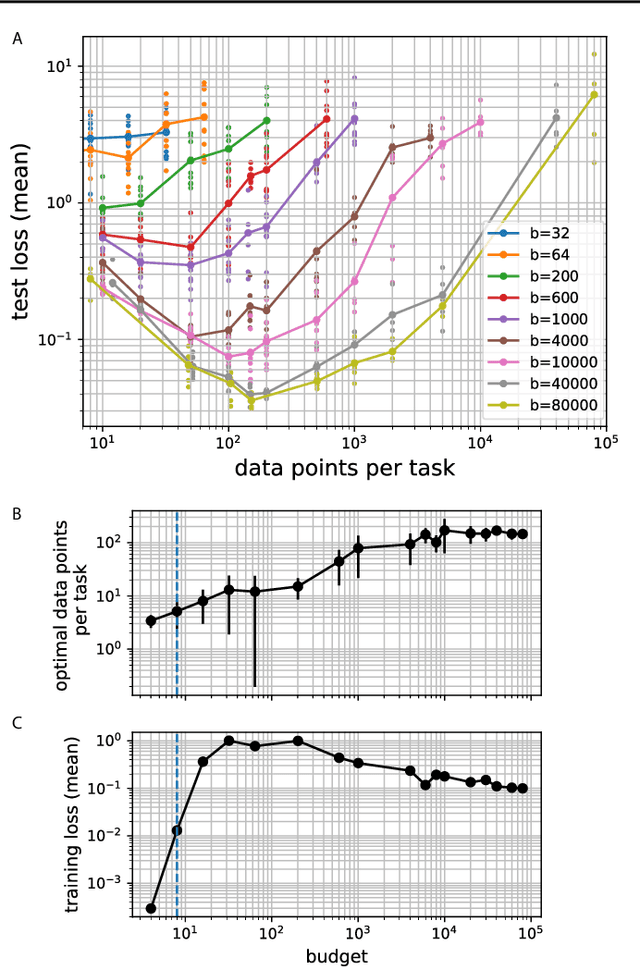
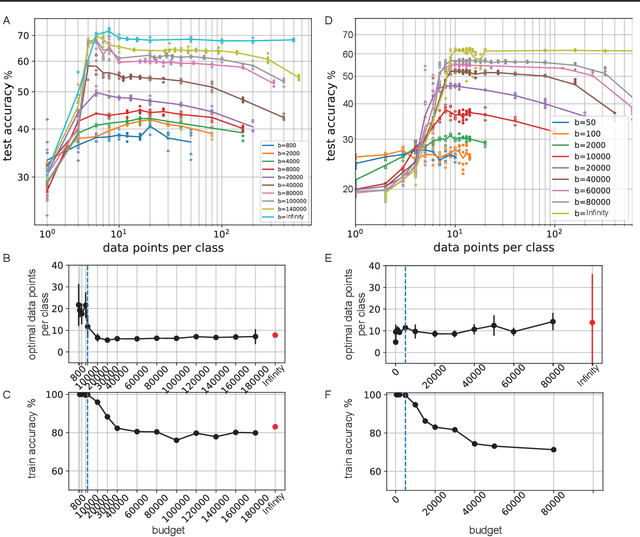
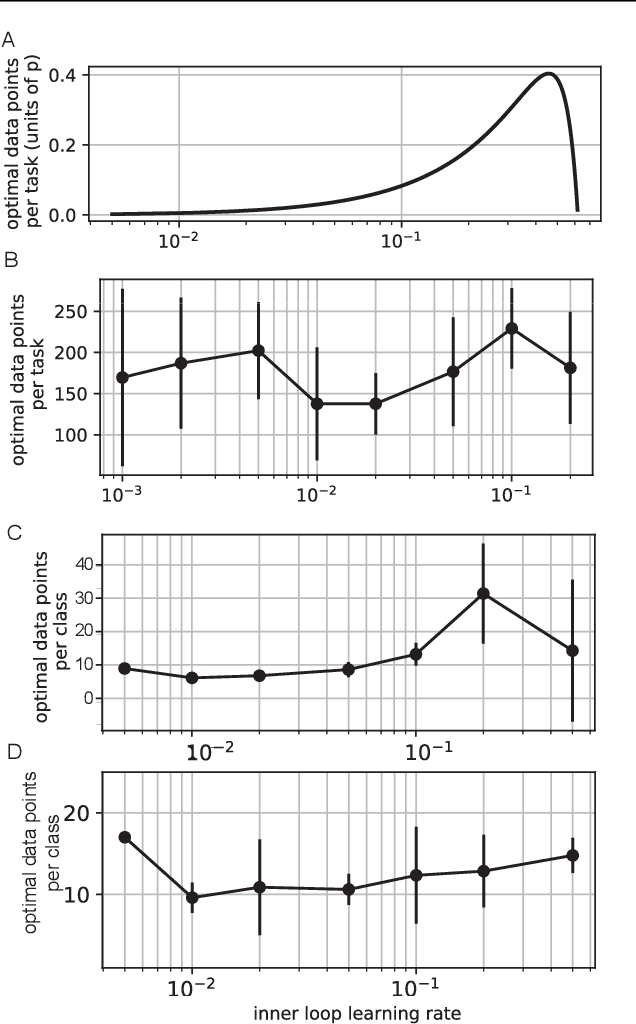
Meta-learning models transfer the knowledge acquired from previous tasks to quickly learn new ones. They are tested on benchmarks with a fixed number of data points per training task. This number is usually arbitrary and it is unknown how it affects the performance. Since labelling of data is expensive, finding the optimal allocation of labels across training tasks may reduce costs: given a fixed budget of labels, should we use a small number of highly labelled tasks, or many tasks with few labels each? We show that: 1) The optimal number of data points per task depends on the budget, but it converges to a unique constant value for large budgets; 2) Convergence occurs around the interpolation threshold of the model. We prove our results mathematically on mixed linear regression, and we show empirically that the same results hold for nonlinear regression and few-shot image classification on CIFAR-FS and mini-ImageNet. Our results suggest a simple and efficient procedure for data collection: the optimal allocation of data can be computed at low cost, by using relatively small data, and collection of additional data can be optimized by the knowledge of the optimal allocation.