Unraveling Arithmetic in Large Language Models: The Role of Algebraic Structures

Large language models (LLMs) have demonstrated remarkable mathematical capabilities, largely driven by chain-of-thought (CoT) prompting, which decomposes complex reasoning into step-by-step solutions. This approach has enabled significant advancements, as evidenced by performance on benchmarks like GSM8K and MATH. However, the mechanisms underlying LLMs' ability to perform arithmetic in a single step of CoT remain poorly understood. Existing studies debate whether LLMs encode numerical values or rely on symbolic reasoning, while others explore attention and multi-layered processing in arithmetic tasks. In this work, we propose that LLMs learn arithmetic by capturing algebraic structures, such as \emph{Commutativity} and \emph{Identity} properties. Since these structures are observable through input-output relationships, they can generalize to unseen data. We empirically demonstrate that LLMs can learn algebraic structures using a custom dataset of arithmetic problems. Our findings indicate that leveraging algebraic structures can enhance the LLMs' arithmetic capabilities, offering insights into improving their arithmetic performance.

RL-STaR: Theoretical Analysis of Reinforcement Learning Frameworks for Self-Taught Reasoner

The reasoning abilities of large language models (LLMs) have improved with chain-of-thought (CoT) prompting, allowing models to solve complex tasks in a stepwise manner. However, training CoT capabilities requires detailed reasoning data, which is often scarce. The self-taught reasoner (STaR) framework addresses this by using reinforcement learning to automatically generate reasoning steps, reducing reliance on human-labeled data. Although STaR and its variants have demonstrated empirical success, a theoretical foundation explaining these improvements is lacking. This work provides a theoretical framework for understanding the effectiveness of reinforcement learning on CoT reasoning and STaR. Our contributions are: (1) an analysis of policy improvement, showing why LLM reasoning improves iteratively with STaR; (2) conditions for convergence to an optimal reasoning policy; (3) an examination of STaR's robustness, explaining how it can improve reasoning even when incorporating occasional incorrect steps; and (4) criteria for the quality of pre-trained models necessary to initiate effective reasoning improvement. This framework aims to bridge empirical findings with theoretical insights, advancing reinforcement learning approaches for reasoning in LLMs.

Leveraging Unlabeled Data Sharing through Kernel Function Approximation in Offline Reinforcement Learning

Offline reinforcement learning (RL) learns policies from a fixed dataset, but often requires large amounts of data. The challenge arises when labeled datasets are expensive, especially when rewards have to be provided by human labelers for large datasets. In contrast, unlabelled data tends to be less expensive. This situation highlights the importance of finding effective ways to use unlabelled data in offline RL, especially when labelled data is limited or expensive to obtain. In this paper, we present the algorithm to utilize the unlabeled data in the offline RL method with kernel function approximation and give the theoretical guarantee. We present various eigenvalue decay conditions of $\mathcal{H}_k$ which determine the complexity of the algorithm. In summary, our work provides a promising approach for exploiting the advantages offered by unlabeled data in offline RL, whilst maintaining theoretical assurances.

Sample Complexity of Kernel-Based Q-Learning

Modern reinforcement learning (RL) often faces an enormous state-action space. Existing analytical results are typically for settings with a small number of state-actions, or simple models such as linearly modeled Q-functions. To derive statistically efficient RL policies handling large state-action spaces, with more general Q-functions, some recent works have considered nonlinear function approximation using kernel ridge regression. In this work, we derive sample complexities for kernel based Q-learning when a generative model exists. We propose a nonparametric Q-learning algorithm which finds an $\epsilon$-optimal policy in an arbitrarily large scale discounted MDP. The sample complexity of the proposed algorithm is order optimal with respect to $\epsilon$ and the complexity of the kernel (in terms of its information gain). To the best of our knowledge, this is the first result showing a finite sample complexity under such a general model.

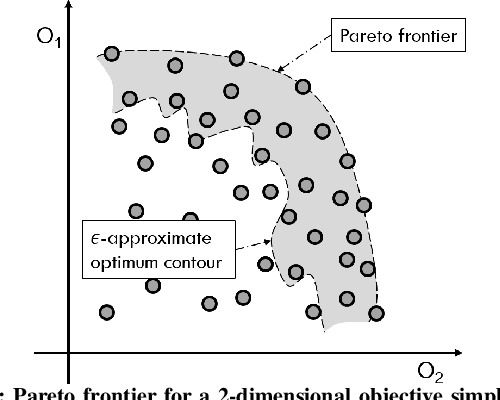
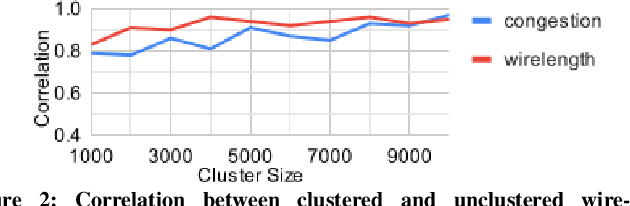
Flexible Multiple-Objective Reinforcement Learning for Chip Placement

Recently, successful applications of reinforcement learning to chip placement have emerged. Pretrained models are necessary to improve efficiency and effectiveness. Currently, the weights of objective metrics (e.g., wirelength, congestion, and timing) are fixed during pretraining. However, fixed-weighed models cannot generate the diversity of placements required for engineers to accommodate changing requirements as they arise. This paper proposes flexible multiple-objective reinforcement learning (MORL) to support objective functions with inference-time variable weights using just a single pretrained model. Our macro placement results show that MORL can generate the Pareto frontier of multiple objectives effectively.

G2R Bound: A Generalization Bound for Supervised Learning from GAN-Synthetic Data

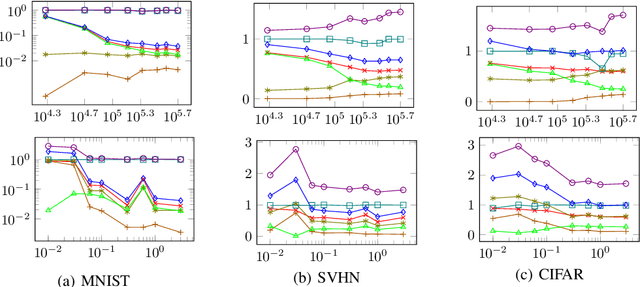
Performing supervised learning from the data synthesized by using Generative Adversarial Networks (GANs), dubbed GAN-synthetic data, has two important applications. First, GANs may generate more labeled training data, which may help improve classification accuracy. Second, in scenarios where real data cannot be released outside certain premises for privacy and/or security reasons, using GAN- synthetic data to conduct training is a plausible alternative. This paper proposes a generalization bound to guarantee the generalization capability of a classifier learning from GAN-synthetic data. This generalization bound helps developers gauge the generalization gap between learning from synthetic data and testing on real data, and can therefore provide the clues to improve the generalization capability.

Representation Learning on Large and Small Data

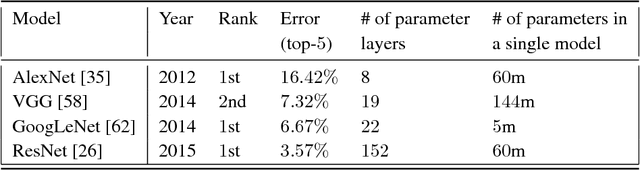
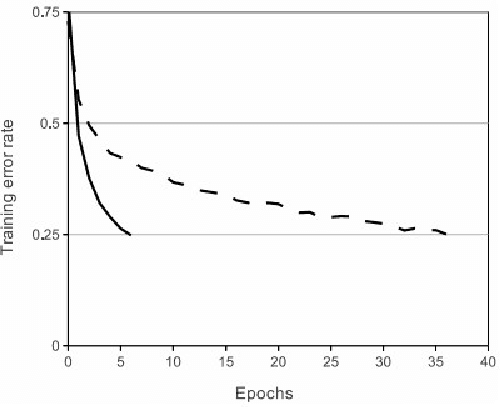
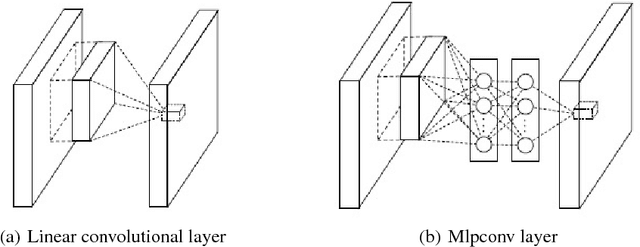
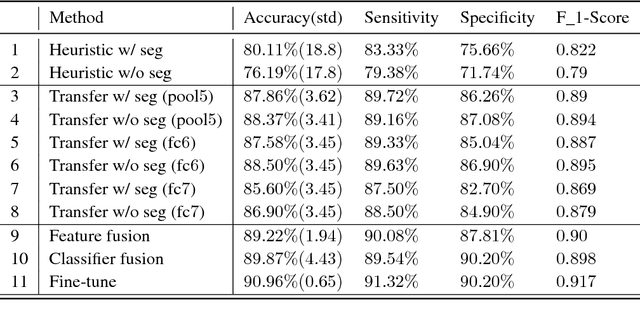
Deep learning owes its success to three key factors: scale of data, enhanced models to learn representations from data, and scale of computation. This book chapter presented the importance of the data-driven approach to learn good representations from both big data and small data. In terms of big data, it has been widely accepted in the research community that the more data the better for both representation and classification improvement. The question is then how to learn representations from big data, and how to perform representation learning when data is scarce. We addressed the first question by presenting CNN model enhancements in the aspects of representation, optimization, and generalization. To address the small data challenge, we showed transfer representation learning to be effective. Transfer representation learning transfers the learned representation from a source domain where abundant training data is available to a target domain where training data is scarce. Transfer representation learning gave the OM and melanoma diagnosis modules of our XPRIZE Tricorder device (which finished $2^{nd}$ out of $310$ competing teams) a significant boost in diagnosis accuracy.