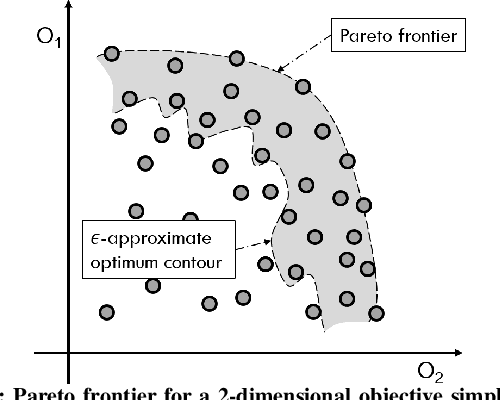
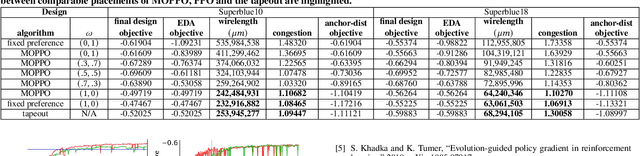
Flexible Multiple-Objective Reinforcement Learning for Chip Placement

Recently, successful applications of reinforcement learning to chip placement have emerged. Pretrained models are necessary to improve efficiency and effectiveness. Currently, the weights of objective metrics (e.g., wirelength, congestion, and timing) are fixed during pretraining. However, fixed-weighed models cannot generate the diversity of placements required for engineers to accommodate changing requirements as they arise. This paper proposes flexible multiple-objective reinforcement learning (MORL) to support objective functions with inference-time variable weights using just a single pretrained model. Our macro placement results show that MORL can generate the Pareto frontier of multiple objectives effectively.

Combined Independent Component Analysis and Canonical Polyadic Decomposition via Joint Diagonalization

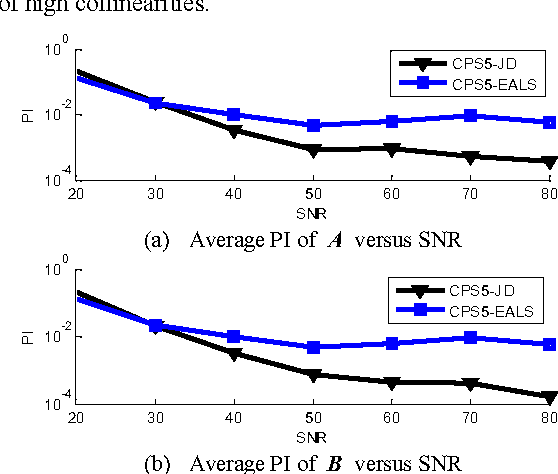
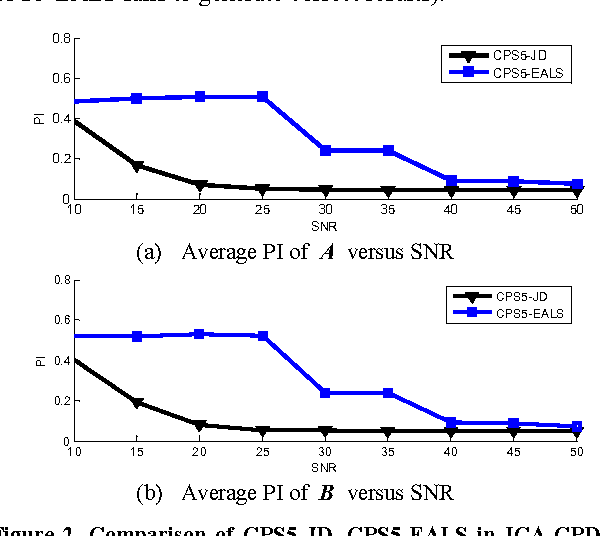
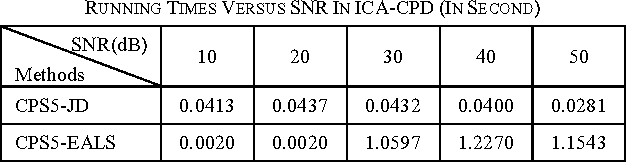
Recently, there has been a trend to combine independent component analysis and canonical polyadic decomposition (ICA-CPD) for an enhanced robustness for the computation of CPD, and ICA-CPD could be further converted into CPD of a 5th-order partially symmetric tensor, by calculating the eigenmatrices of the 4th-order cumulant slices of a trilinear mixture. In this study, we propose a new 5th-order CPD algorithm constrained with partial symmetry based on joint diagonalization. As the main steps involved in the proposed algorithm undergo no updating iterations for the loading matrices, it is much faster than the existing algorithm based on alternating least squares and enhanced line search, with competent performances. Simulation results are provided to demonstrate the performance of the proposed algorithm.