Xiao-Feng Gong
Target Localization with Coprime Multistatic MIMO Radar via Coupled Canonical Polyadic Decomposition Based on Joint Eigenvalue Decomposition
May 28, 2025Abstract:This paper investigates target localization using a multistatic multiple-input multiple-output (MIMO) radar system with two distinct coprime array configurations: coprime L-shaped arrays and coprime planar arrays. The observed signals are modeled as tensors that admit a coupled canonical polyadic decomposition (C-CPD) model. For each configuration, a C-CPD method is presented based on joint eigenvalue decomposition (J-EVD). This computational framework includes (semi-)algebraic and optimization-based C-CPD algorithms and target localization that fuses direction-of-arrivals (DOAs) information to calculate the optimal position of each target. Specifically, the proposed (semi-)algebraic methods exploit the rotational invariance of the Vandermonde structure in coprime arrays, similar to the multiple invariance property of \added{estimation of signal parameters via rotational invariance techniques} (ESPRIT), which transforms the model into a J-EVD problem and reduces computational complexity. The study also investigates the working conditions of the algorithm to understand model identifiability. Additionally, the proposed method does not rely on prior knowledge of non-orthogonal probing waveforms and is effective in challenging underdetermined scenarios. Experimental results demonstrate that our method outperforms existing tensor-based approaches in both accuracy and computational efficiency.
A Block Term Decomposition Model Based Algorithm for Tensor Completion of Multidimensional Harmonic Signals
Jan 25, 2025

Abstract:We consider tensor data completion of an incomplete observation of multidimensional harmonic (MH) signals. Unlike existing tensor-based techniques for MH retrieval (MHR), which mostly adopt the canonical polyadic decomposition (CPD) to model the simple "one-to-one" correspondence among harmonics across difference modes, we herein use the more flexible block term decomposition (BTD) model that can be used to describe the complex mutual correspondences among several groups of harmonics across different modes. An optimization principle that aims to fit the BTD model in the least squares sense, subject to rank minimization of hankelized MH components, is set up for the tensor completion task, and an algorithm based on alternating direction method of multipliers is proposed, of which the effectiveness and applicability are validated through both numerical simulations and an application in Sub-6GHz channel state information (CSI) completion.
A parametric non-negative coupled canonical polyadic decomposition algorithm for hyperspectral super-resolution
Jan 25, 2025



Abstract:Recently, coupled tensor decomposition has been widely used in data fusion of a hyperspectral image (HSI) and a multispectral image (MSI) for hyperspectral super-resolution (HSR). However, exsiting works often ignore the inherent non-negative (NN) property of the image data, or impose the NN constraint via hard-thresholding which may interfere with the optimization procedure and cause the method to be sub-optimal. As such, we propose a novel NN coupled canonical polyadic decomposition (NN-C-CPD) algorithm, which makes use of the parametric method and nonlinear least squares (NLS) framework to impose the NN constraint into the C-CPD computation. More exactly, the NN constraint is converted into the squared relationship between the NN entries of the factor matrices and a set of latent parameters. Based on the chain rule for deriving the derivatives, the key entities such as gradient and Jacobian with regards to the latent parameters can be derived, thus the NN constraint is naturally integrated without interfering with the optimization procedure. Experimental results are provided to demonstrate the performance of the proposed NN-C-CPD algorithm in HSR applications.
Target Localization with a Coprime Multistatic MIMO Radar via Coupled Canonical Polyadic Decomposition Based on Joint EVD
Jan 25, 2025
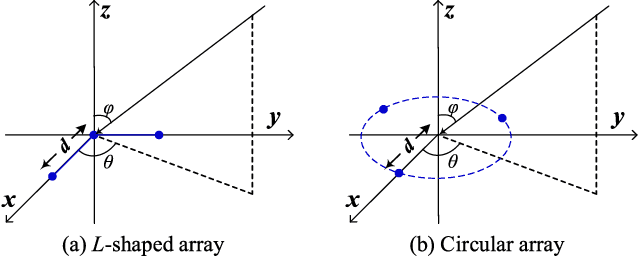
Abstract:This paper addresses target localization using a multistatic multiple-input multiple-output (MIMO) radar system with coprime L-shaped receive arrays (CLsA). A target localization method is proposed by modeling the observed signals as tensors that admit a coupled canonical polyadic decomposition (C-CPD) model without matched filtering. It consists of a novel joint eigenvalue decomposition (J-EVD) based (semi-)algebraic algorithm, and a post-processing approach to determine the target locations by fusing the direction-of-arrival estimates extracted from J-EVD-based CCPD results. Particularly, by leveraging the rotational invariance of Vandermonde structure in CLsA, we convert the CCPD problem into a J-EVD problem, significantly reducing its computational complexity. Experimental results show that our method outperforms existing tensor-based ones.
A Coupled Random Projection Approach to Large-Scale Canonical Polyadic Decomposition
May 10, 2021
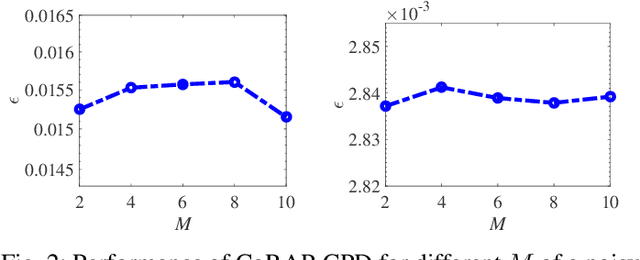
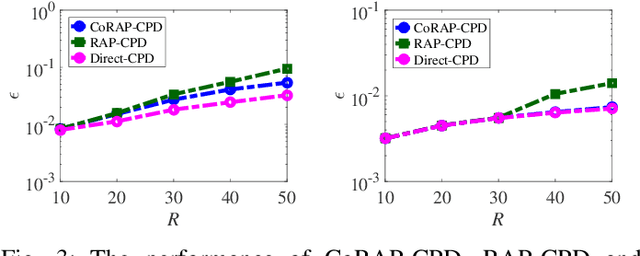
Abstract:We propose a novel algorithm for the computation of canonical polyadic decomposition (CPD) of large-scale tensors. The proposed algorithm generalizes the random projection (RAP) technique, which is often used to compute large-scale decompositions, from one single projection to multiple but coupled random projections (CoRAP). The proposed CoRAP technique yields a set of tensors that together admits a coupled CPD (C-CPD) and a C-CPD algorithm is then used to jointly decompose these tensors. The results of C-CPD are finally fused to obtain factor matrices of the original large-scale data tensor. As more data samples are jointly exploited via C-CPD, the proposed CoRAP based CPD is more accurate than RAP based CPD. Experiments are provided to illustrate the performance of the proposed approach.
Double Coupled Canonical Polyadic Decomposition for Joint Blind Source Separation
Apr 28, 2018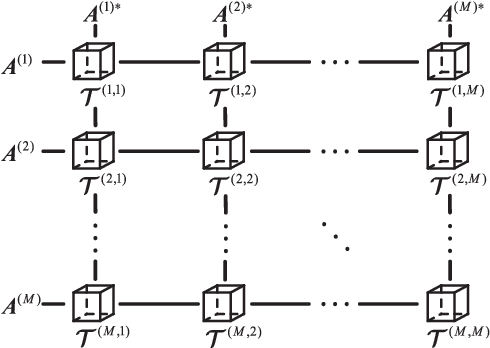
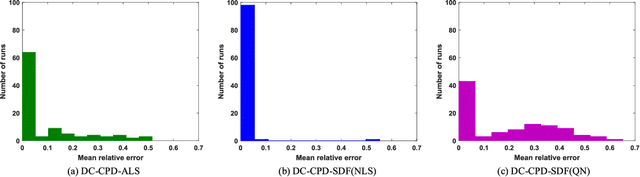
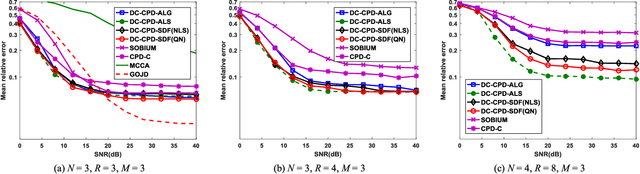
Abstract:Joint blind source separation (J-BSS) is an emerging data-driven technique for multi-set data-fusion. In this paper, J-BSS is addressed from a tensorial perspective. We show how, by using second-order multi-set statistics in J-BSS, a specific double coupled canonical polyadic decomposition (DC-CPD) problem can be formulated. We propose an algebraic DC-CPD algorithm based on a coupled rank-1 detection mapping. This algorithm converts a possibly underdetermined DC-CPD to a set of overdetermined CPDs. The latter can be solved algebraically via a generalized eigenvalue decomposition based scheme. Therefore, this algorithm is deterministic and returns the exact solution in the noiseless case. In the noisy case, it can be used to effectively initialize optimization based DC-CPD algorithms. In addition, we obtain the determini- stic and generic uniqueness conditions for DC-CPD, which are shown to be more relaxed than their CPD counterpart. Experiment results are given to illustrate the superiority of DC-CPD over standard CPD based BSS methods and several existing J-BSS methods, with regards to uniqueness and accuracy.
Combined Independent Component Analysis and Canonical Polyadic Decomposition via Joint Diagonalization
Dec 28, 2016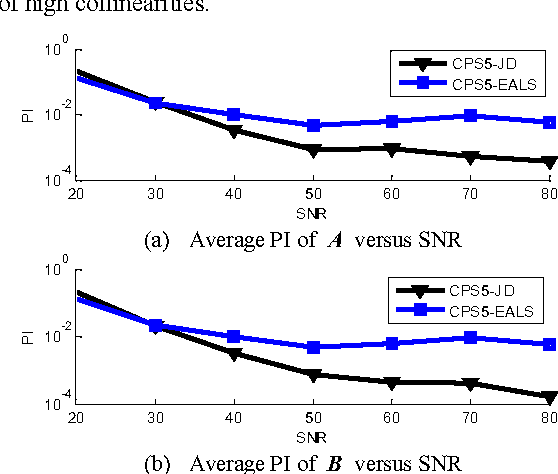
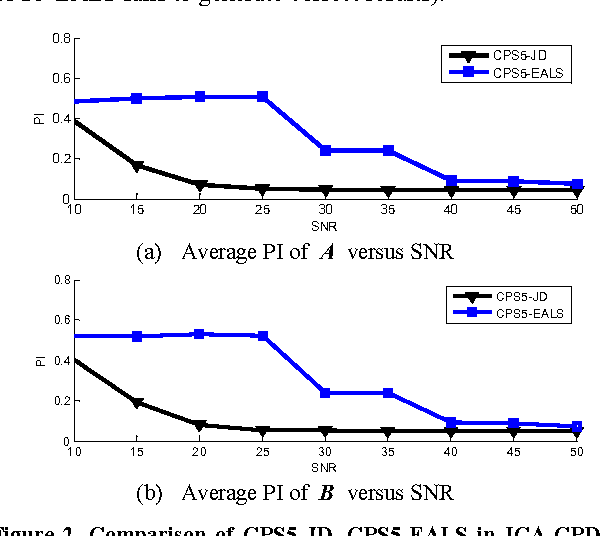
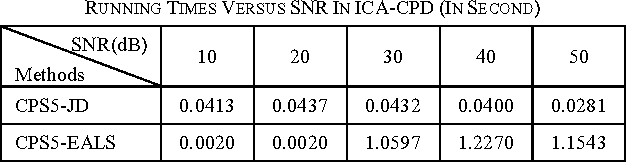
Abstract:Recently, there has been a trend to combine independent component analysis and canonical polyadic decomposition (ICA-CPD) for an enhanced robustness for the computation of CPD, and ICA-CPD could be further converted into CPD of a 5th-order partially symmetric tensor, by calculating the eigenmatrices of the 4th-order cumulant slices of a trilinear mixture. In this study, we propose a new 5th-order CPD algorithm constrained with partial symmetry based on joint diagonalization. As the main steps involved in the proposed algorithm undergo no updating iterations for the loading matrices, it is much faster than the existing algorithm based on alternating least squares and enhanced line search, with competent performances. Simulation results are provided to demonstrate the performance of the proposed algorithm.
Generalized Non-orthogonal Joint Diagonalization with LU Decomposition and Successive Rotations
Feb 12, 2015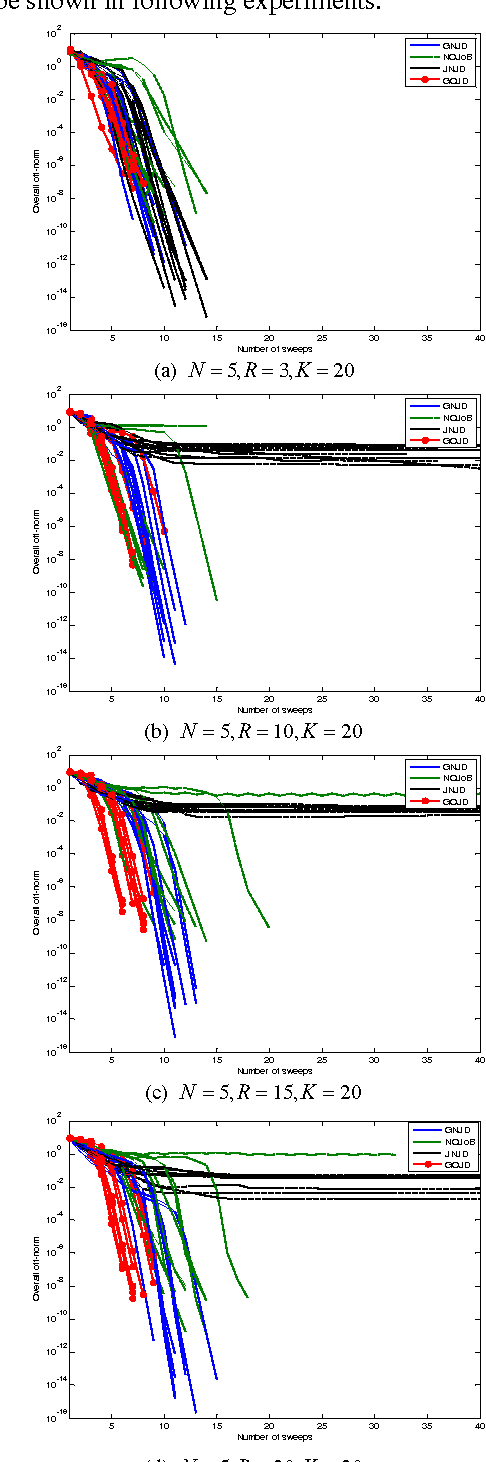
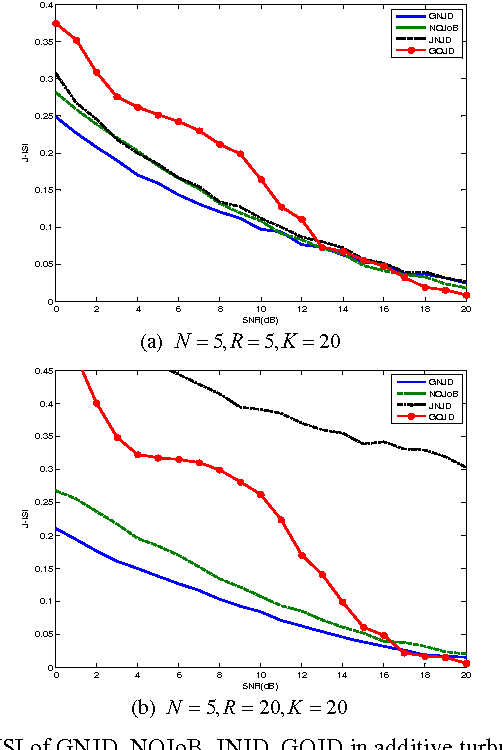
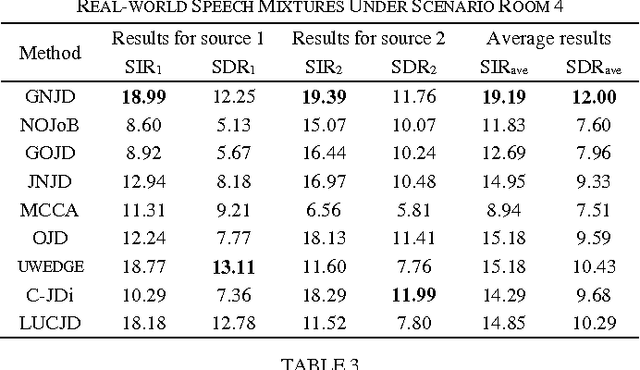
Abstract:Non-orthogonal joint diagonalization (NJD) free of prewhitening has been widely studied in the context of blind source separation (BSS) and array signal processing, etc. However, NJD is used to retrieve the jointly diagonalizable structure for a single set of target matrices which are mostly formulized with a single dataset, and thus is insufficient to handle multiple datasets with inter-set dependences, a scenario often encountered in joint BSS (J-BSS) applications. As such, we present a generalized NJD (GNJD) algorithm to simultaneously perform asymmetric NJD upon multiple sets of target matrices with mutually linked loading matrices, by using LU decomposition and successive rotations, to enable J-BSS over multiple datasets with indication/exploitation of their mutual dependences. Experiments with synthetic and real-world datasets are provided to illustrate the performance of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge