Least-squares methods for nonnegative matrix factorization over rational functions

Nonnegative Matrix Factorization (NMF) models are widely used to recover linearly mixed nonnegative data. When the data is made of samplings of continuous signals, the factors in NMF can be constrained to be samples of nonnegative rational functions, which allow fairly general models; this is referred to as NMF using rational functions (R-NMF). We first show that, under mild assumptions, R-NMF has an essentially unique factorization unlike NMF, which is crucial in applications where ground-truth factors need to be recovered such as blind source separation problems. Then we present different approaches to solve R-NMF: the R-HANLS, R-ANLS and R-NLS methods. From our tests, no method significantly outperforms the others, and a trade-off should be done between time and accuracy. Indeed, R-HANLS is fast and accurate for large problems, while R-ANLS is more accurate, but also more resources demanding, both in time and memory. R-NLS is very accurate but only for small problems. Moreover, we show that R-NMF outperforms NMF in various tasks including the recovery of semi-synthetic continuous signals, and a classification problem of real hyperspectral signals.

Factorizer: A Scalable Interpretable Approach to Context Modeling for Medical Image Segmentation

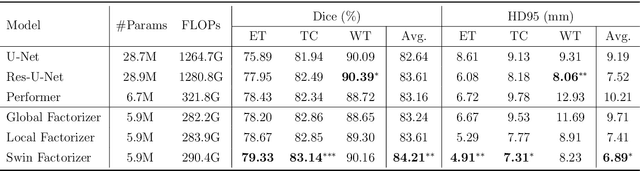
Convolutional Neural Networks (CNNs) with U-shaped architectures have dominated medical image segmentation, which is crucial for various clinical purposes. However, the inherent locality of convolution makes CNNs fail to fully exploit global context, essential for better recognition of some structures, e.g., brain lesions. Transformers have recently proved promising performance on vision tasks, including semantic segmentation, mainly due to their capability of modeling long-range dependencies. Nevertheless, the quadratic complexity of attention makes existing Transformer-based models use self-attention layers only after somehow reducing the image resolution, which limits the ability to capture global contexts present at higher resolutions. Therefore, this work introduces a family of models, dubbed Factorizer, which leverages the power of low-rank matrix factorization for constructing an end-to-end segmentation model. Specifically, we propose a linearly scalable approach to context modeling, formulating Nonnegative Matrix Factorization (NMF) as a differentiable layer integrated into a U-shaped architecture. The shifted window technique is also utilized in combination with NMF to effectively aggregate local information. Factorizers compete favorably with CNNs and Transformers in terms of accuracy, scalability, and interpretability, achieving state-of-the-art results on the BraTS dataset for brain tumor segmentation, with Dice scores of 79.33%, 83.14%, and 90.16% for enhancing tumor, tumor core, and whole tumor, respectively. Highly meaningful NMF components give an additional interpretability advantage to Factorizers over CNNs and Transformers. Moreover, our ablation studies reveal a distinctive feature of Factorizers that enables a significant speed-up in inference for a trained Factorizer without any extra steps and without sacrificing much accuracy.

Nonconvex Optimization Tools for Large-Scale Matrix and Tensor Decomposition with Structured Factors

The proposed article aims at offering a comprehensive tutorial for the computational aspects of structured matrix and tensor factorization. Unlike existing tutorials that mainly focus on {\it algorithmic procedures} for a small set of problems, e.g., nonnegativity or sparsity-constrained factorization, we take a {\it top-down} approach: we start with general optimization theory (e.g., inexact and accelerated block coordinate descent, stochastic optimization, and Gauss-Newton methods) that covers a wide range of factorization problems with diverse constraints and regularization terms of engineering interest. Then, we go `under the hood' to showcase specific algorithm design under these introduced principles. We pay a particular attention to recent algorithmic developments in structured tensor and matrix factorization (e.g., random sketching and adaptive step size based stochastic optimization and structure-exploiting second-order algorithms), which are the state of the art---yet much less touched upon in the literature compared to {\it block coordinate descent} (BCD)-based methods. We expect that the article to have an educational values in the field of structured factorization and hope to stimulate more research in this important and exciting direction.

Early soft and flexible fusion of EEG and fMRI via tensor decompositions

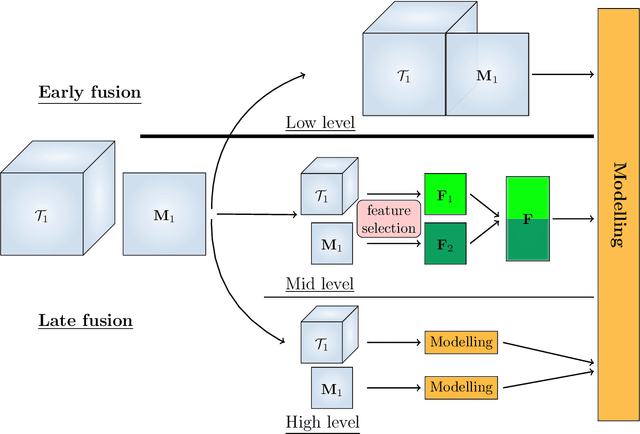
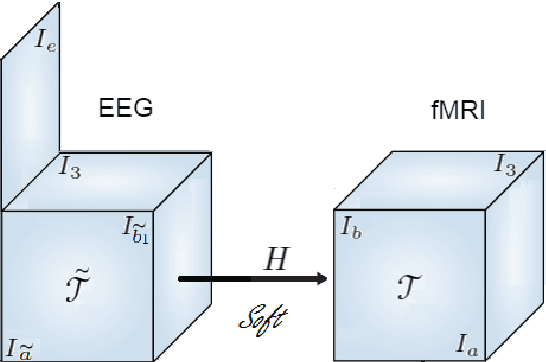
Data fusion refers to the joint analysis of multiple datasets which provide complementary views of the same task. In this preprint, the problem of jointly analyzing electroencephalography (EEG) and functional Magnetic Resonance Imaging (fMRI) data is considered. Jointly analyzing EEG and fMRI measurements is highly beneficial for studying brain function because these modalities have complementary spatiotemporal resolution: EEG offers good temporal resolution while fMRI is better in its spatial resolution. The fusion methods reported so far ignore the underlying multi-way nature of the data in at least one of the modalities and/or rely on very strong assumptions about the relation of the two datasets. In this preprint, these two points are addressed by adopting for the first time tensor models in the two modalities while also exploring double coupled tensor decompositions and by following soft and flexible coupling approaches to implement the multi-modal analysis. To cope with the Event Related Potential (ERP) variability in EEG, the PARAFAC2 model is adopted. The results obtained are compared against those of parallel Independent Component Analysis (ICA) and hard coupling alternatives in both simulated and real data. Our results confirm the superiority of tensorial methods over methods based on ICA. In scenarios that do not meet the assumptions underlying hard coupling, the advantage of soft and flexible coupled decompositions is clearly demonstrated.

Double Coupled Canonical Polyadic Decomposition for Joint Blind Source Separation

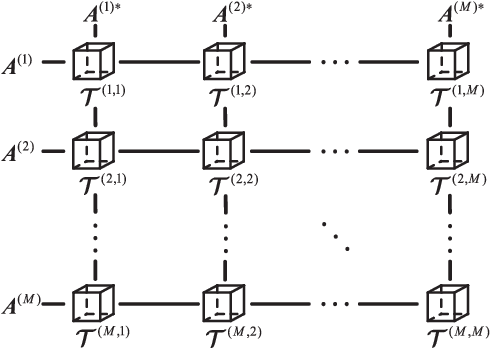
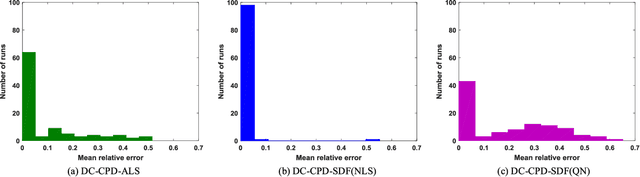
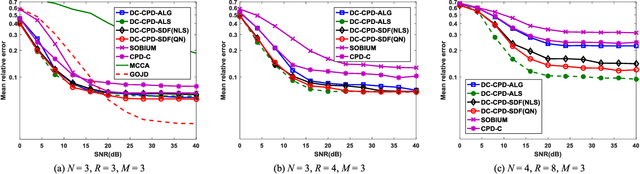
Joint blind source separation (J-BSS) is an emerging data-driven technique for multi-set data-fusion. In this paper, J-BSS is addressed from a tensorial perspective. We show how, by using second-order multi-set statistics in J-BSS, a specific double coupled canonical polyadic decomposition (DC-CPD) problem can be formulated. We propose an algebraic DC-CPD algorithm based on a coupled rank-1 detection mapping. This algorithm converts a possibly underdetermined DC-CPD to a set of overdetermined CPDs. The latter can be solved algebraically via a generalized eigenvalue decomposition based scheme. Therefore, this algorithm is deterministic and returns the exact solution in the noiseless case. In the noisy case, it can be used to effectively initialize optimization based DC-CPD algorithms. In addition, we obtain the determini- stic and generic uniqueness conditions for DC-CPD, which are shown to be more relaxed than their CPD counterpart. Experiment results are given to illustrate the superiority of DC-CPD over standard CPD based BSS methods and several existing J-BSS methods, with regards to uniqueness and accuracy.

Tensor Decomposition for Signal Processing and Machine Learning

Tensors or {\em multi-way arrays} are functions of three or more indices $(i,j,k,\cdots)$ -- similar to matrices (two-way arrays), which are functions of two indices $(r,c)$ for (row,column). Tensors have a rich history, stretching over almost a century, and touching upon numerous disciplines; but they have only recently become ubiquitous in signal and data analytics at the confluence of signal processing, statistics, data mining and machine learning. This overview article aims to provide a good starting point for researchers and practitioners interested in learning about and working with tensors. As such, it focuses on fundamentals and motivation (using various application examples), aiming to strike an appropriate balance of breadth {\em and depth} that will enable someone having taken first graduate courses in matrix algebra and probability to get started doing research and/or developing tensor algorithms and software. Some background in applied optimization is useful but not strictly required. The material covered includes tensor rank and rank decomposition; basic tensor factorization models and their relationships and properties (including fairly good coverage of identifiability); broad coverage of algorithms ranging from alternating optimization to stochastic gradient; statistical performance analysis; and applications ranging from source separation to collaborative filtering, mixture and topic modeling, classification, and multilinear subspace learning.

Learning Tensors in Reproducing Kernel Hilbert Spaces with Multilinear Spectral Penalties

We present a general framework to learn functions in tensor product reproducing kernel Hilbert spaces (TP-RKHSs). The methodology is based on a novel representer theorem suitable for existing as well as new spectral penalties for tensors. When the functions in the TP-RKHS are defined on the Cartesian product of finite discrete sets, in particular, our main problem formulation admits as a special case existing tensor completion problems. Other special cases include transfer learning with multimodal side information and multilinear multitask learning. For the latter case, our kernel-based view is instrumental to derive nonlinear extensions of existing model classes. We give a novel algorithm and show in experiments the usefulness of the proposed extensions.