Tensor-based Channel Tracking for RIS-Empowered Multi-User MIMO Wireless Systems

The accurate estimation of Channel State Information (CSI) is of crucial importance for the successful operation of Multiple-Input Multiple-Output (MIMO) communication systems, especially in a Multi-User (MU) time-varying environment and when employing the emerging technology of Reconfigurable Intelligent Surfaces (RISs). Their predominantly passive nature renders the estimation of the channels involved in the user-RIS-base station link a quite challenging problem. Moreover, the time-varying nature of most of the realistic wireless channels drives up the cost of real-time channel tracking significantly, especially when RISs of massive size are deployed. In this paper, we develop a channel tracking scheme for the uplink of RIS-enabled MU MIMO systems in the presence of channel fading. The starting point is a tensor representation of the received signal and we rely on its PARAllel FACtor (PARAFAC) analysis to both get the initial estimate and track the channel time variation. Simulation results for various system settings are reported, which validate the feasibility and effectiveness of the proposed channel tracking approach.

A Bayesian Approach to Block-Term Tensor Decomposition Model Selection and Computation

The so-called block-term decomposition (BTD) tensor model, especially in its rank-$(L_r,L_r,1)$ version, has been recently receiving increasing attention due to its enhanced ability of representing systems and signals that are composed of \emph{blocks} of rank higher than one, a scenario encountered in numerous and diverse applications. Its uniqueness and approximation have thus been thoroughly studied. Nevertheless, the challenging problem of estimating the BTD model structure, namely the number of block terms and their individual ranks, has only recently started to attract significant attention. In this work, a Bayesian approach is taken to addressing the problem of rank-$(L_r,L_r,1)$ BTD model selection and computation, based on the idea of imposing column sparsity \emph{jointly} on the factors and in a \emph{hierarchical} manner and estimating the ranks as the numbers of factor columns of non-negligible energy. Using variational inference in the proposed probabilistic model results in an iterative algorithm that comprises closed-form updates. Its Bayesian nature completely avoids the ubiquitous in regularization-based methods task of hyper-parameter tuning. Simulation results with synthetic data are reported, which demonstrate the effectiveness of the proposed scheme in terms of both rank estimation and model fitting.

Early soft and flexible fusion of EEG and fMRI via tensor decompositions

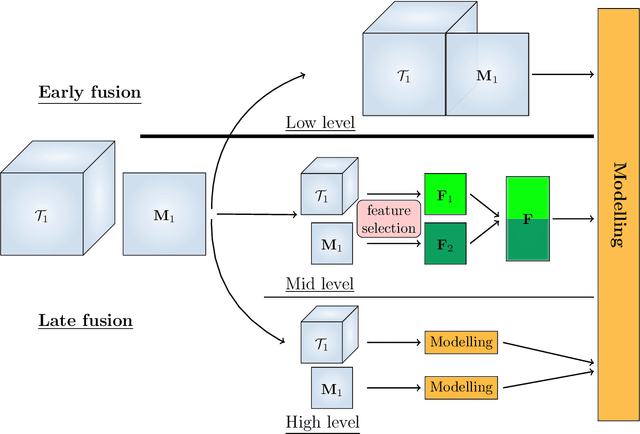
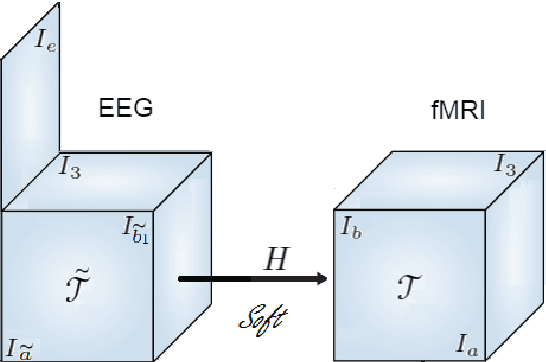
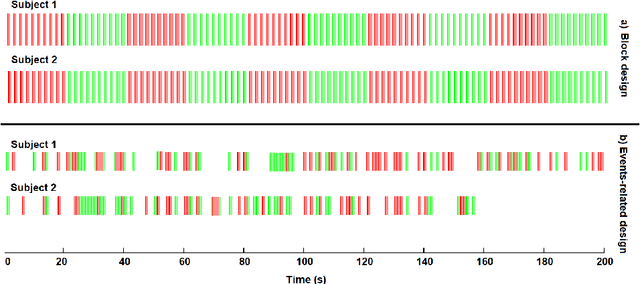
Data fusion refers to the joint analysis of multiple datasets which provide complementary views of the same task. In this preprint, the problem of jointly analyzing electroencephalography (EEG) and functional Magnetic Resonance Imaging (fMRI) data is considered. Jointly analyzing EEG and fMRI measurements is highly beneficial for studying brain function because these modalities have complementary spatiotemporal resolution: EEG offers good temporal resolution while fMRI is better in its spatial resolution. The fusion methods reported so far ignore the underlying multi-way nature of the data in at least one of the modalities and/or rely on very strong assumptions about the relation of the two datasets. In this preprint, these two points are addressed by adopting for the first time tensor models in the two modalities while also exploring double coupled tensor decompositions and by following soft and flexible coupling approaches to implement the multi-modal analysis. To cope with the Event Related Potential (ERP) variability in EEG, the PARAFAC2 model is adopted. The results obtained are compared against those of parallel Independent Component Analysis (ICA) and hard coupling alternatives in both simulated and real data. Our results confirm the superiority of tensorial methods over methods based on ICA. In scenarios that do not meet the assumptions underlying hard coupling, the advantage of soft and flexible coupled decompositions is clearly demonstrated.

Assisted Dictionary Learning for fMRI Data Analysis

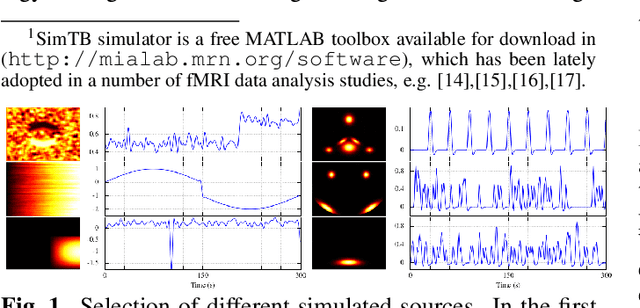
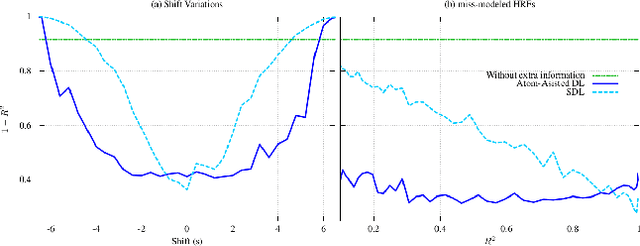
Extracting information from functional magnetic resonance (fMRI) images has been a major area of research for more than two decades. The goal of this work is to present a new method for the analysis of fMRI data sets, that is capable to incorporate a priori available information, via an efficient optimization framework. Tests on synthetic data sets demonstrate significant performance gains over existing methods of this kind.

Higher-Order Block Term Decomposition for Spatially Folded fMRI Data

The growing use of neuroimaging technologies generates a massive amount of biomedical data that exhibit high dimensionality. Tensor-based analysis of brain imaging data has been proved quite effective in exploiting their multiway nature. The advantages of tensorial methods over matrix-based approaches have also been demonstrated in the characterization of functional magnetic resonance imaging (fMRI) data, where the spatial (voxel) dimensions are commonly grouped (unfolded) as a single way/mode of the 3-rd order array, the other two ways corresponding to time and subjects. However, such methods are known to be ineffective in more demanding scenarios, such as the ones with strong noise and/or significant overlapping of activated regions. This paper aims at investigating the possible gains from a better exploitation of the spatial dimension, through a higher- (4 or 5) order tensor modeling of the fMRI signal. In this context, and in order to increase the degrees of freedom of the modeling process, a higher-order Block Term Decomposition (BTD) is applied, for the first time in fMRI analysis. Its effectiveness is demonstrated via extensive simulation results.

Blind Source Separation: Fundamentals and Recent Advances (A Tutorial Overview Presented at SBrT-2001)

Blind source separation (BSS), i.e., the decoupling of unknown signals that have been mixed in an unknown way, has been a topic of great interest in the signal processing community for the last decade, covering a wide range of applications in such diverse fields as digital communications, pattern recognition, biomedical engineering, and financial data analysis, among others. This course aims at an introduction to the BSS problem via an exposition of well-known and established as well as some more recent approaches to its solution. A unified way is followed in presenting the various results so as to more easily bring out their similarities/differences and emphasize their relative advantages/disadvantages. Only a representative sample of the existing knowledge on BSS will be included in this course. The interested readers are encouraged to consult the list of bibliographical references for more details on this exciting and always active research topic.