The Ideal Continual Learner: An Agent That Never Forgets

The goal of continual learning is to find a model that solves multiple learning tasks which are presented sequentially to the learner. A key challenge in this setting is that the learner may forget how to solve a previous task when learning a new task, a phenomenon known as catastrophic forgetting. To address this challenge, many practical methods have been proposed, including memory-based, regularization-based, and expansion-based methods. However, a rigorous theoretical understanding of these methods remains elusive. This paper aims to bridge this gap between theory and practice by proposing a new continual learning framework called Ideal Continual Learner (ICL), which is guaranteed to avoid catastrophic forgetting by construction. We show that ICL unifies multiple well-established continual learning methods and gives new theoretical insights into the strengths and weaknesses of these methods. We also derive generalization bounds for ICL which allow us to theoretically quantify how rehearsal affects generalization. Finally, we connect ICL to several classic subjects and research topics of modern interest, which allows us to make historical remarks and inspire future directions.

Implicit Bias of Projected Subgradient Method Gives Provable Robust Recovery of Subspaces of Unknown Codimension

Robust subspace recovery (RSR) is a fundamental problem in robust representation learning. Here we focus on a recently proposed RSR method termed Dual Principal Component Pursuit (DPCP) approach, which aims to recover a basis of the orthogonal complement of the subspace and is amenable to handling subspaces of high relative dimension. Prior work has shown that DPCP can provably recover the correct subspace in the presence of outliers, as long as the true dimension of the subspace is known. We show that DPCP can provably solve RSR problems in the {\it unknown} subspace dimension regime, as long as orthogonality constraints -- adopted in previous DPCP formulations -- are relaxed and random initialization is used instead of spectral one. Namely, we propose a very simple algorithm based on running multiple instances of a projected sub-gradient descent method (PSGM), with each problem instance seeking to find one vector in the null space of the subspace. We theoretically prove that under mild conditions this approach will succeed with high probability. In particular, we show that 1) all of the problem instances will converge to a vector in the nullspace of the subspace and 2) the ensemble of problem instance solutions will be sufficiently diverse to fully span the nullspace of the subspace thus also revealing its true unknown codimension. We provide empirical results that corroborate our theoretical results and showcase the remarkable implicit rank regularization behavior of PSGM algorithm that allows us to perform RSR without being aware of the subspace dimension.

A Bayesian Approach to Block-Term Tensor Decomposition Model Selection and Computation

The so-called block-term decomposition (BTD) tensor model, especially in its rank-$(L_r,L_r,1)$ version, has been recently receiving increasing attention due to its enhanced ability of representing systems and signals that are composed of \emph{blocks} of rank higher than one, a scenario encountered in numerous and diverse applications. Its uniqueness and approximation have thus been thoroughly studied. Nevertheless, the challenging problem of estimating the BTD model structure, namely the number of block terms and their individual ranks, has only recently started to attract significant attention. In this work, a Bayesian approach is taken to addressing the problem of rank-$(L_r,L_r,1)$ BTD model selection and computation, based on the idea of imposing column sparsity \emph{jointly} on the factors and in a \emph{hierarchical} manner and estimating the ranks as the numbers of factor columns of non-negligible energy. Using variational inference in the proposed probabilistic model results in an iterative algorithm that comprises closed-form updates. Its Bayesian nature completely avoids the ubiquitous in regularization-based methods task of hyper-parameter tuning. Simulation results with synthetic data are reported, which demonstrate the effectiveness of the proposed scheme in terms of both rank estimation and model fitting.

Alternating Iteratively Reweighted Minimization Algorithms for Low-Rank Matrix Factorization

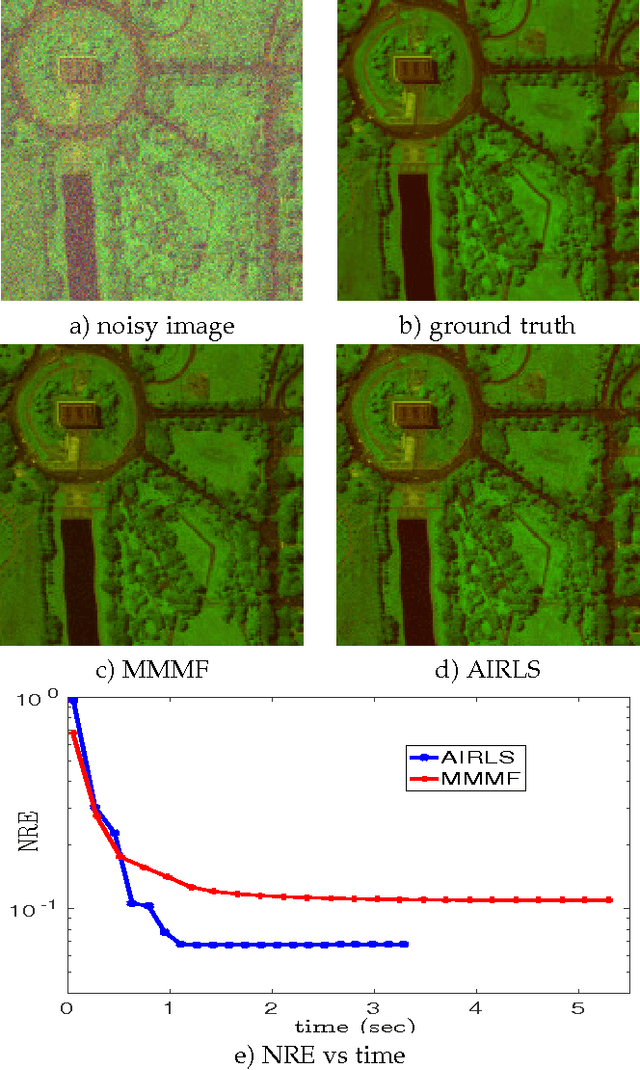
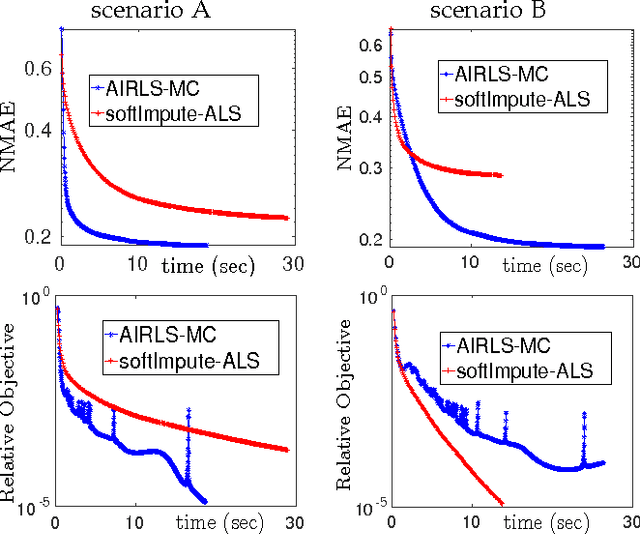
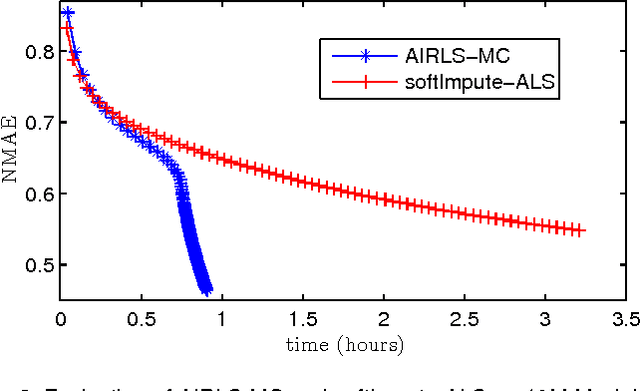
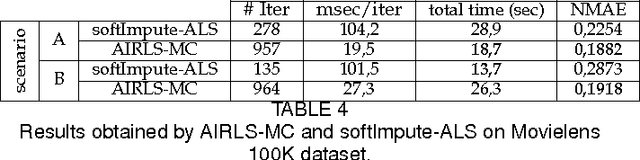
Nowadays, the availability of large-scale data in disparate application domains urges the deployment of sophisticated tools for extracting valuable knowledge out of this huge bulk of information. In that vein, low-rank representations (LRRs) which seek low-dimensional embeddings of data have naturally appeared. In an effort to reduce computational complexity and improve estimation performance, LRR has been viewed via a matrix factorization (MF) perspective. Recently, low-rank MF (LRMF) approaches have been proposed for tackling the inherent weakness of MF i.e., the unawareness of the dimension of the low-dimensional space where data reside. Herein, inspired by the merits of iterative reweighted schemes for rank minimization, we come up with a generic low-rank promoting regularization function. Then, focusing on a specific instance of it, we propose a regularizer that imposes column-sparsity jointly on the two matrix factors that result from MF, thus promoting low-rankness on the optimization problem. The problems of denoising, matrix completion and non-negative matrix factorization (NMF) are redefined according to the new LRMF formulation and solved via efficient Newton-type algorithms with proven theoretical guarantees as to their convergence and rates of convergence to stationary points. The effectiveness of the proposed algorithms is verified in diverse simulated and real data experiments.

Low-rank and Sparse NMF for Joint Endmembers' Number Estimation and Blind Unmixing of Hyperspectral Images

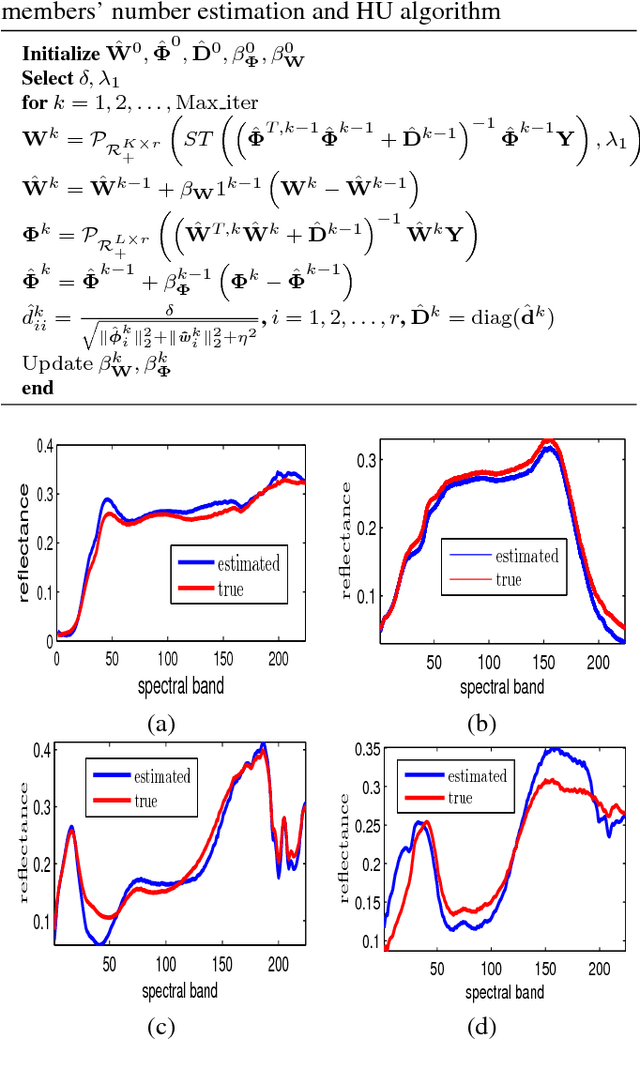
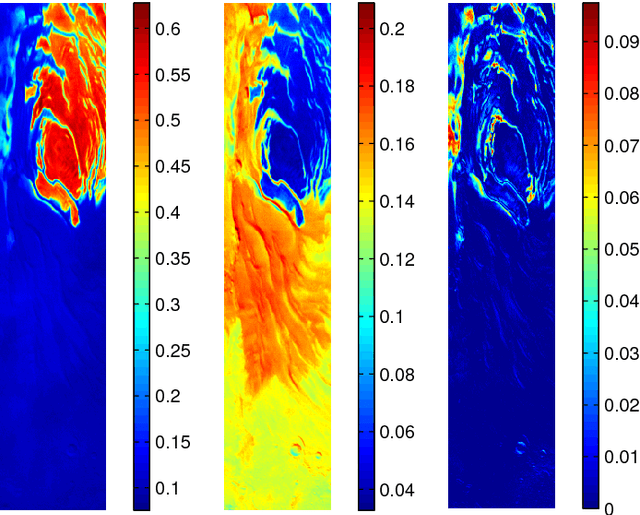
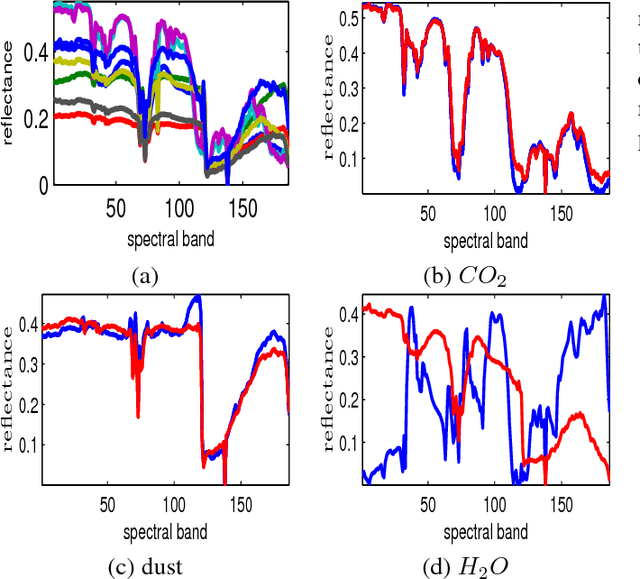
Estimation of the number of endmembers existing in a scene constitutes a critical task in the hyperspectral unmixing process. The accuracy of this estimate plays a crucial role in subsequent unsupervised unmixing steps i.e., the derivation of the spectral signatures of the endmembers (endmembers' extraction) and the estimation of the abundance fractions of the pixels. A common practice amply followed in literature is to treat endmembers' number estimation and unmixing, independently as two separate tasks, providing the outcome of the former as input to the latter. In this paper, we go beyond this computationally demanding strategy. More precisely, we set forth a multiple constrained optimization framework, which encapsulates endmembers' number estimation and unsupervised unmixing in a single task. This is attained by suitably formulating the problem via a low-rank and sparse nonnegative matrix factorization rationale, where low-rankness is promoted with the use of a sophisticated $\ell_2/\ell_1$ norm penalty term. An alternating proximal algorithm is then proposed for minimizing the emerging cost function. The results obtained by simulated and real data experiments verify the effectiveness of the proposed approach.

Online Low-Rank Subspace Learning from Incomplete Data: A Bayesian View

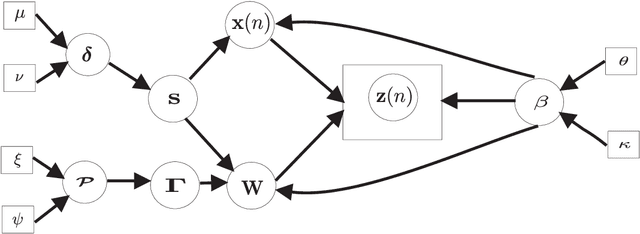
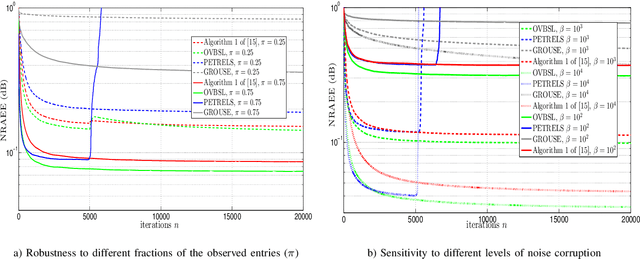
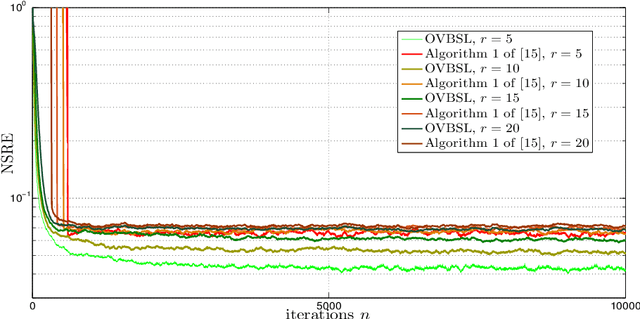
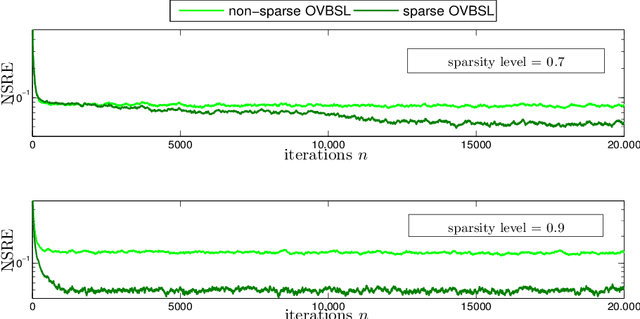
Extracting the underlying low-dimensional space where high-dimensional signals often reside has long been at the center of numerous algorithms in the signal processing and machine learning literature during the past few decades. At the same time, working with incomplete (partly observed) large scale datasets has recently been commonplace for diverse reasons. This so called {\it big data era} we are currently living calls for devising online subspace learning algorithms that can suitably handle incomplete data. Their envisaged objective is to {\it recursively} estimate the unknown subspace by processing streaming data sequentially, thus reducing computational complexity, while obviating the need for storing the whole dataset in memory. In this paper, an online variational Bayes subspace learning algorithm from partial observations is presented. To account for the unawareness of the true rank of the subspace, commonly met in practice, low-rankness is explicitly imposed on the sought subspace data matrix by exploiting sparse Bayesian learning principles. Moreover, sparsity, {\it simultaneously} to low-rankness, is favored on the subspace matrix by the sophisticated hierarchical Bayesian scheme that is adopted. In doing so, the proposed algorithm becomes adept in dealing with applications whereby the underlying subspace may be also sparse, as, e.g., in sparse dictionary learning problems. As shown, the new subspace tracking scheme outperforms its state-of-the-art counterparts in terms of estimation accuracy, in a variety of experiments conducted on simulated and real data.