Low-rank and Sparse NMF for Joint Endmembers' Number Estimation and Blind Unmixing of Hyperspectral Images
Paper and Code
Mar 16, 2017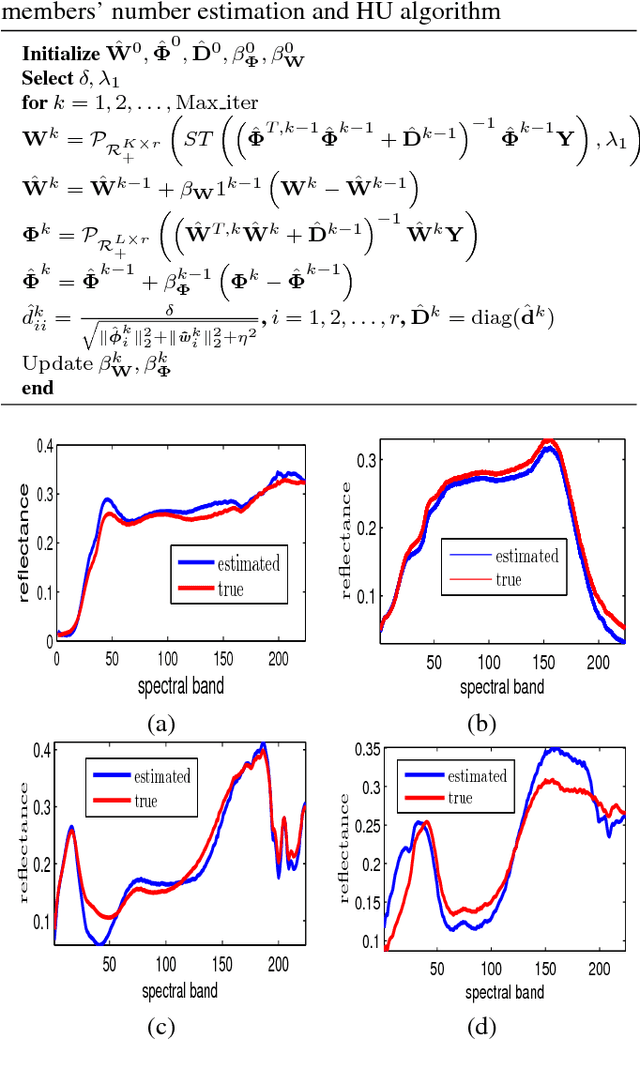
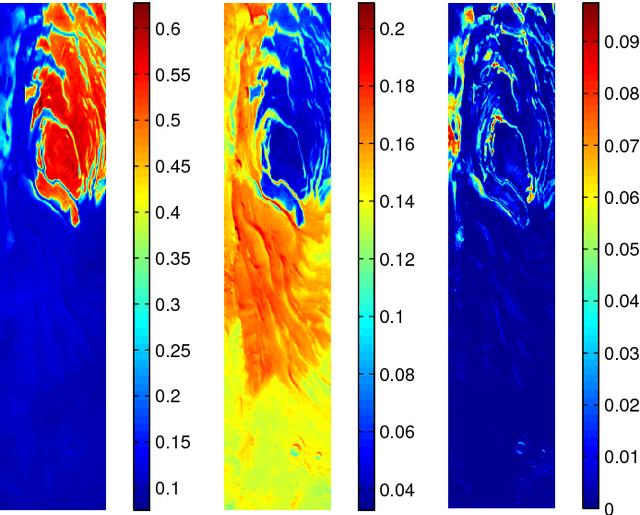
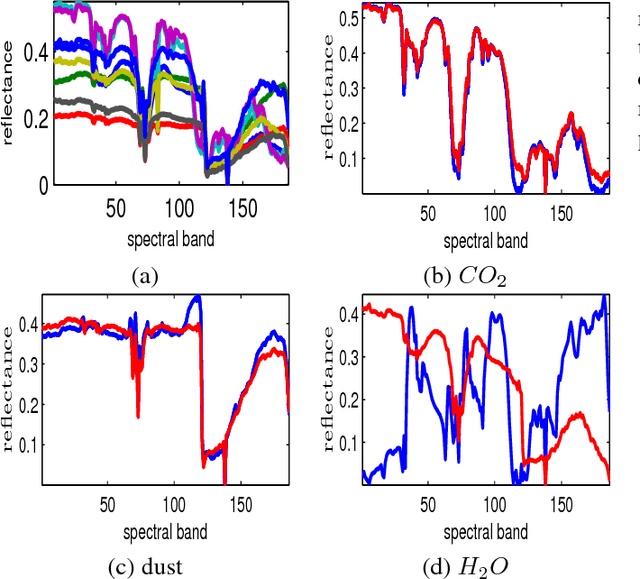
Estimation of the number of endmembers existing in a scene constitutes a critical task in the hyperspectral unmixing process. The accuracy of this estimate plays a crucial role in subsequent unsupervised unmixing steps i.e., the derivation of the spectral signatures of the endmembers (endmembers' extraction) and the estimation of the abundance fractions of the pixels. A common practice amply followed in literature is to treat endmembers' number estimation and unmixing, independently as two separate tasks, providing the outcome of the former as input to the latter. In this paper, we go beyond this computationally demanding strategy. More precisely, we set forth a multiple constrained optimization framework, which encapsulates endmembers' number estimation and unsupervised unmixing in a single task. This is attained by suitably formulating the problem via a low-rank and sparse nonnegative matrix factorization rationale, where low-rankness is promoted with the use of a sophisticated $\ell_2/\ell_1$ norm penalty term. An alternating proximal algorithm is then proposed for minimizing the emerging cost function. The results obtained by simulated and real data experiments verify the effectiveness of the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge