Alternating Iteratively Reweighted Minimization Algorithms for Low-Rank Matrix Factorization

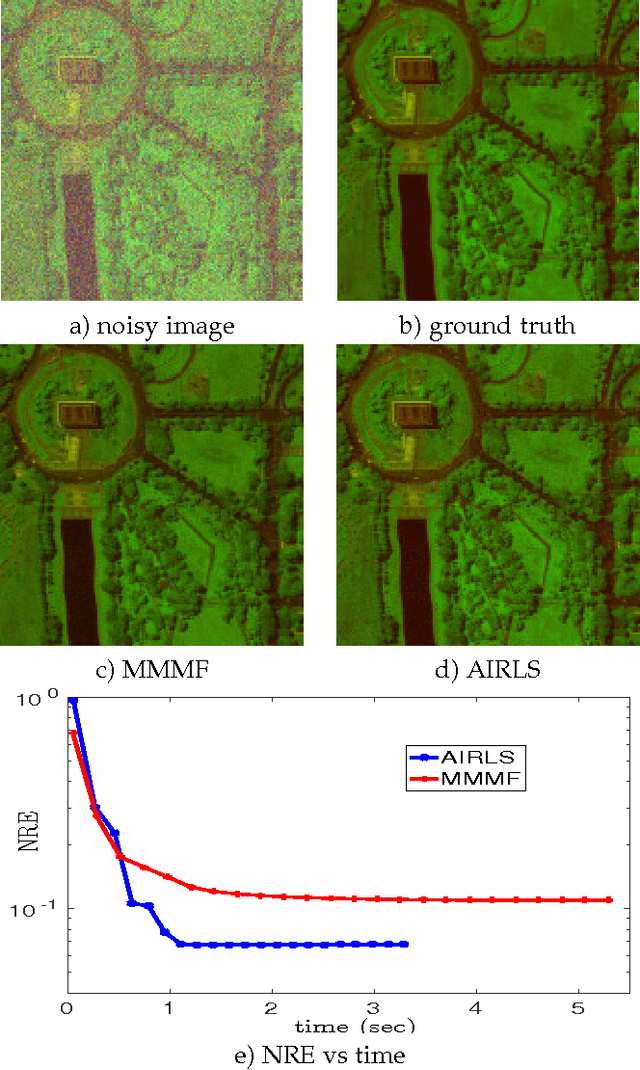
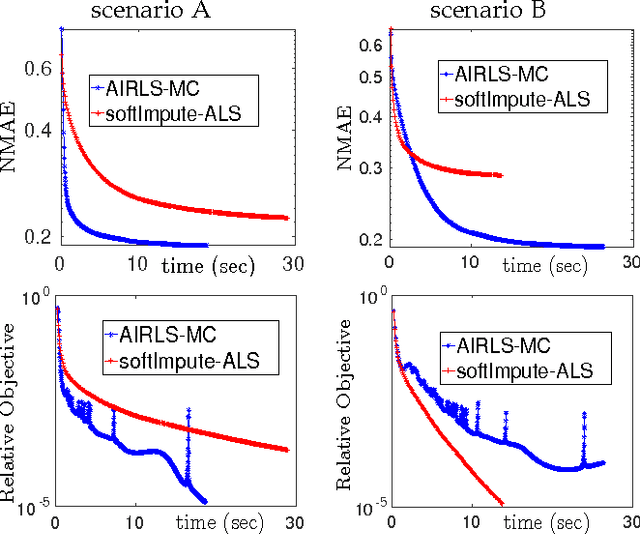
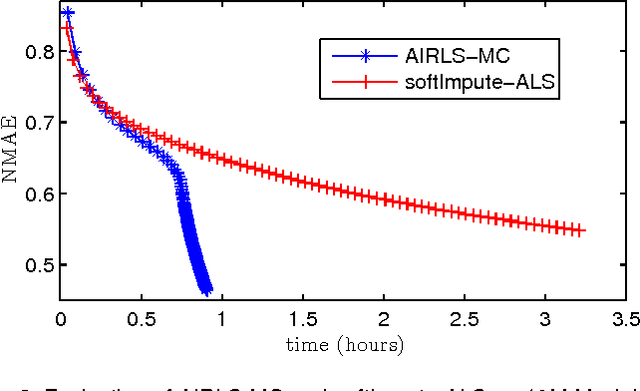
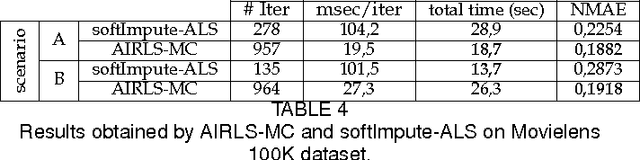
Nowadays, the availability of large-scale data in disparate application domains urges the deployment of sophisticated tools for extracting valuable knowledge out of this huge bulk of information. In that vein, low-rank representations (LRRs) which seek low-dimensional embeddings of data have naturally appeared. In an effort to reduce computational complexity and improve estimation performance, LRR has been viewed via a matrix factorization (MF) perspective. Recently, low-rank MF (LRMF) approaches have been proposed for tackling the inherent weakness of MF i.e., the unawareness of the dimension of the low-dimensional space where data reside. Herein, inspired by the merits of iterative reweighted schemes for rank minimization, we come up with a generic low-rank promoting regularization function. Then, focusing on a specific instance of it, we propose a regularizer that imposes column-sparsity jointly on the two matrix factors that result from MF, thus promoting low-rankness on the optimization problem. The problems of denoising, matrix completion and non-negative matrix factorization (NMF) are redefined according to the new LRMF formulation and solved via efficient Newton-type algorithms with proven theoretical guarantees as to their convergence and rates of convergence to stationary points. The effectiveness of the proposed algorithms is verified in diverse simulated and real data experiments.

On the convergence of the sparse possibilistic c-means algorithm

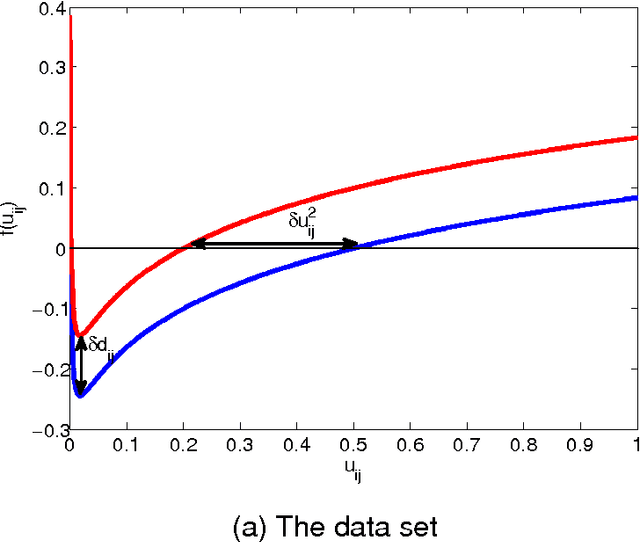
In this paper, a convergence proof for the recently proposed sparse possibilistic c-means (SPCM) algorithm is provided, utilizing the celebrated Zangwill convergence theorem. It is shown that the iterative sequence generated by SPCM converges to a stationary point or there exists a subsequence of it that converges to a stationary point of the cost function of the algorithm.

Low-rank and Sparse NMF for Joint Endmembers' Number Estimation and Blind Unmixing of Hyperspectral Images

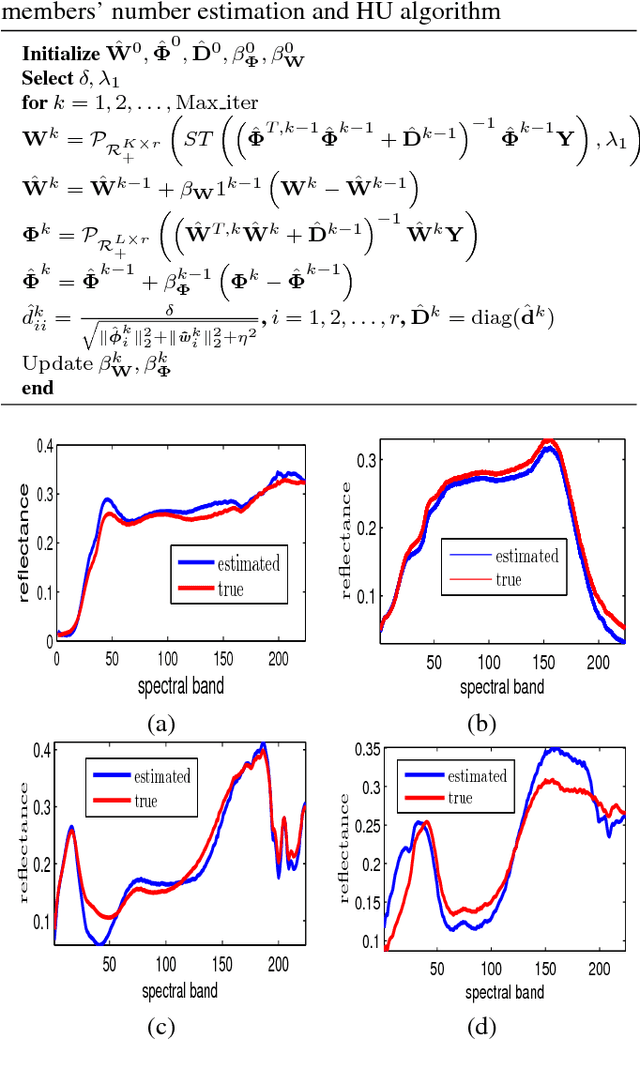
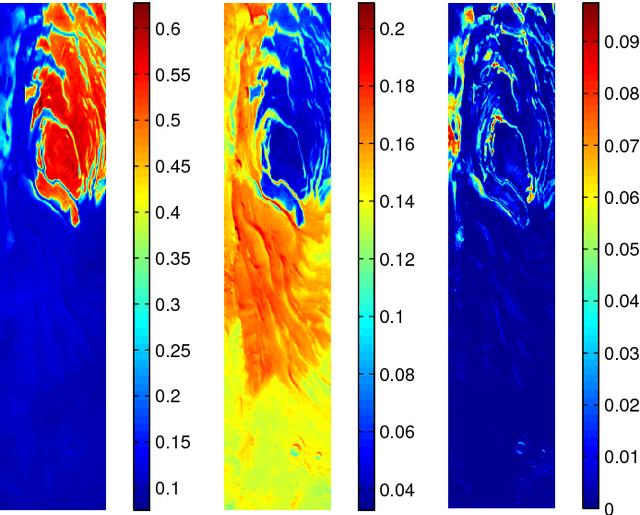
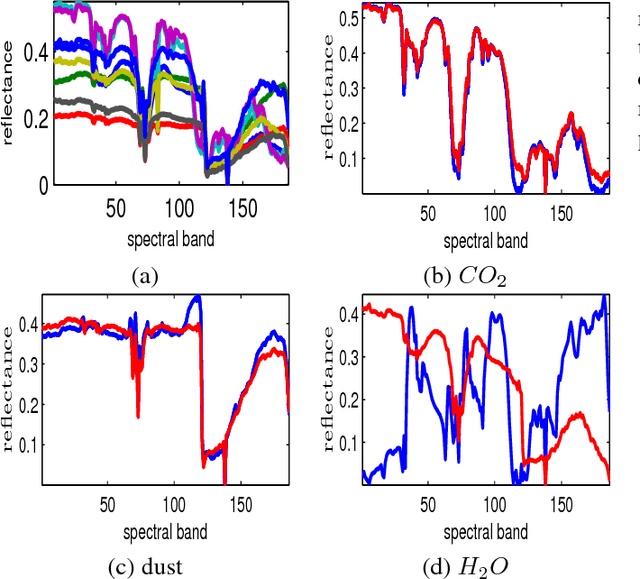
Estimation of the number of endmembers existing in a scene constitutes a critical task in the hyperspectral unmixing process. The accuracy of this estimate plays a crucial role in subsequent unsupervised unmixing steps i.e., the derivation of the spectral signatures of the endmembers (endmembers' extraction) and the estimation of the abundance fractions of the pixels. A common practice amply followed in literature is to treat endmembers' number estimation and unmixing, independently as two separate tasks, providing the outcome of the former as input to the latter. In this paper, we go beyond this computationally demanding strategy. More precisely, we set forth a multiple constrained optimization framework, which encapsulates endmembers' number estimation and unsupervised unmixing in a single task. This is attained by suitably formulating the problem via a low-rank and sparse nonnegative matrix factorization rationale, where low-rankness is promoted with the use of a sophisticated $\ell_2/\ell_1$ norm penalty term. An alternating proximal algorithm is then proposed for minimizing the emerging cost function. The results obtained by simulated and real data experiments verify the effectiveness of the proposed approach.

Online Low-Rank Subspace Learning from Incomplete Data: A Bayesian View

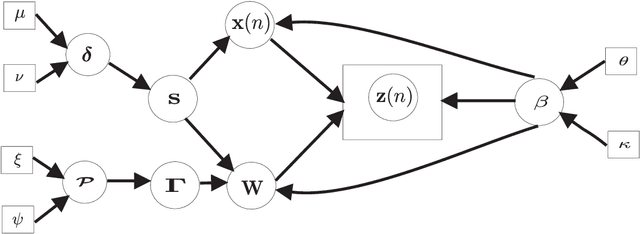
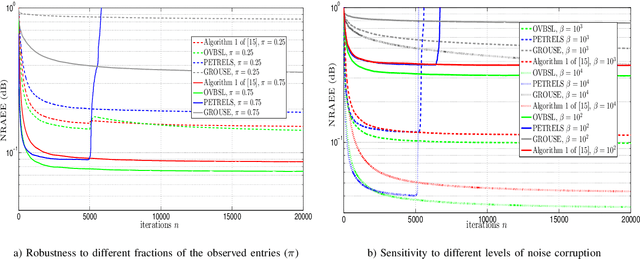
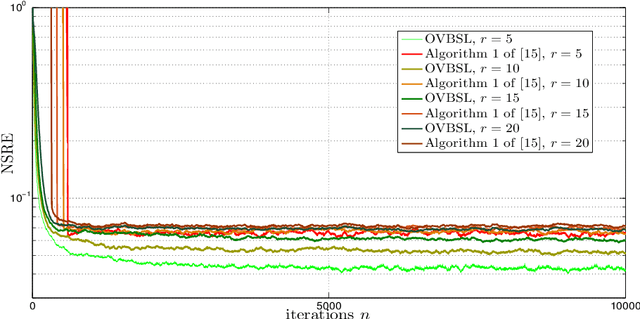
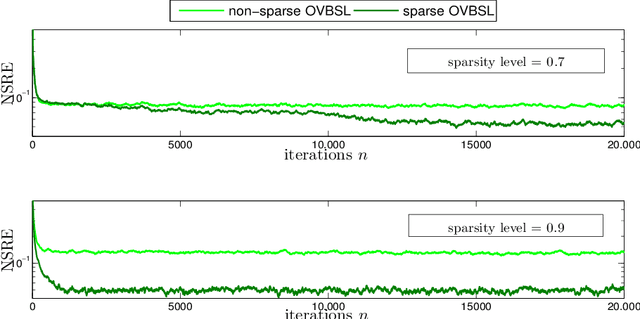
Extracting the underlying low-dimensional space where high-dimensional signals often reside has long been at the center of numerous algorithms in the signal processing and machine learning literature during the past few decades. At the same time, working with incomplete (partly observed) large scale datasets has recently been commonplace for diverse reasons. This so called {\it big data era} we are currently living calls for devising online subspace learning algorithms that can suitably handle incomplete data. Their envisaged objective is to {\it recursively} estimate the unknown subspace by processing streaming data sequentially, thus reducing computational complexity, while obviating the need for storing the whole dataset in memory. In this paper, an online variational Bayes subspace learning algorithm from partial observations is presented. To account for the unawareness of the true rank of the subspace, commonly met in practice, low-rankness is explicitly imposed on the sought subspace data matrix by exploiting sparse Bayesian learning principles. Moreover, sparsity, {\it simultaneously} to low-rankness, is favored on the subspace matrix by the sophisticated hierarchical Bayesian scheme that is adopted. In doing so, the proposed algorithm becomes adept in dealing with applications whereby the underlying subspace may be also sparse, as, e.g., in sparse dictionary learning problems. As shown, the new subspace tracking scheme outperforms its state-of-the-art counterparts in terms of estimation accuracy, in a variety of experiments conducted on simulated and real data.

Sparsity-aware Possibilistic Clustering Algorithms

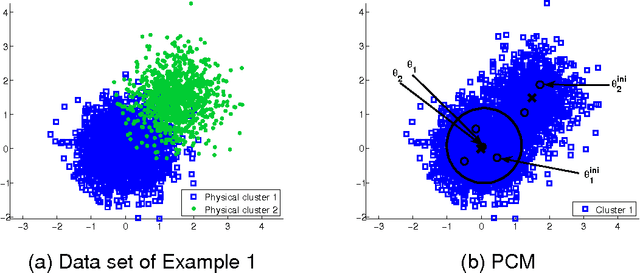
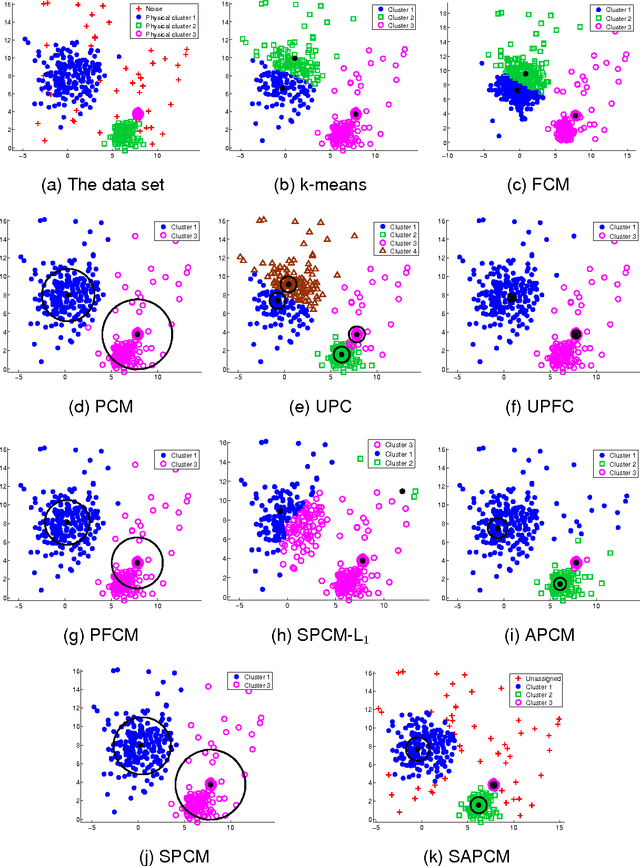
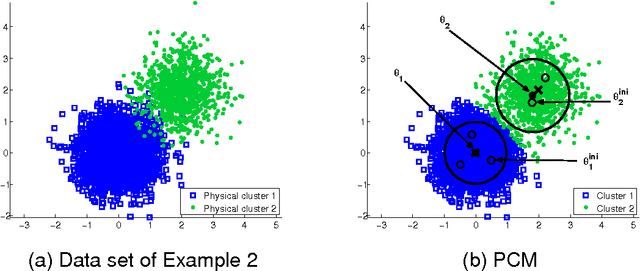
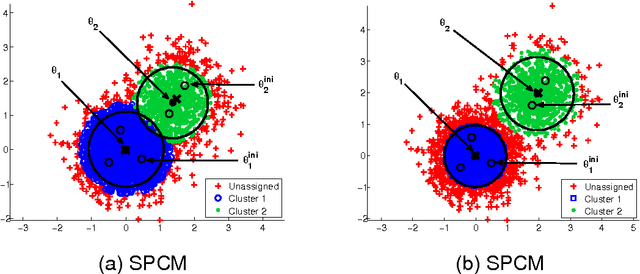
In this paper two novel possibilistic clustering algorithms are presented, which utilize the concept of sparsity. The first one, called sparse possibilistic c-means, exploits sparsity and can deal well with closely located clusters that may also be of significantly different densities. The second one, called sparse adaptive possibilistic c-means, is an extension of the first, where now the involved parameters are dynamically adapted. The latter can deal well with even more challenging cases, where, in addition to the above, clusters may be of significantly different variances. More specifically, it provides improved estimates of the cluster representatives, while, in addition, it has the ability to estimate the actual number of clusters, given an overestimate of it. Extensive experimental results on both synthetic and real data sets support the previous statements.

A Novel Adaptive Possibilistic Clustering Algorithm

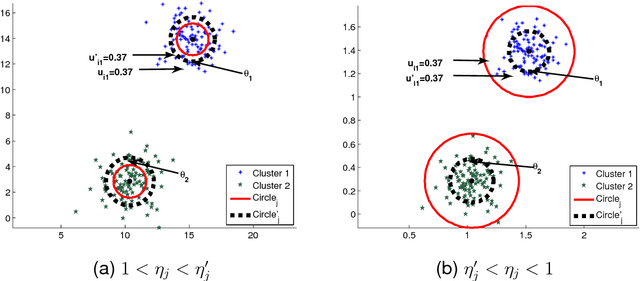
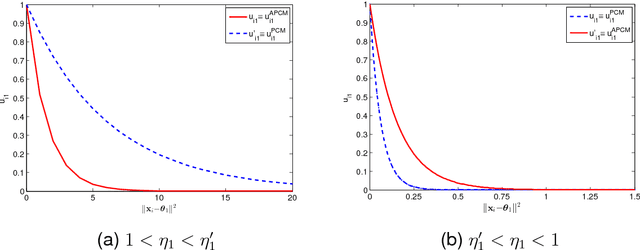
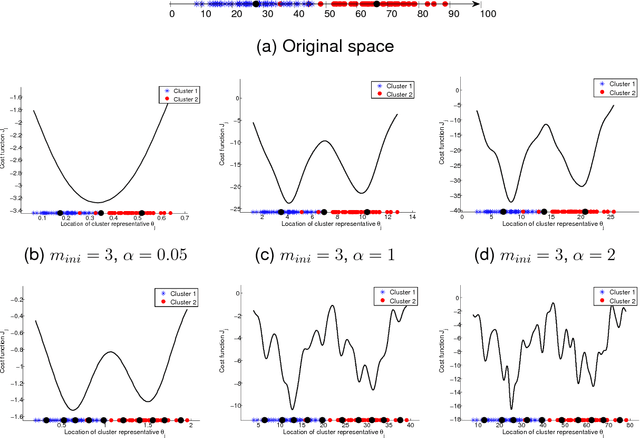
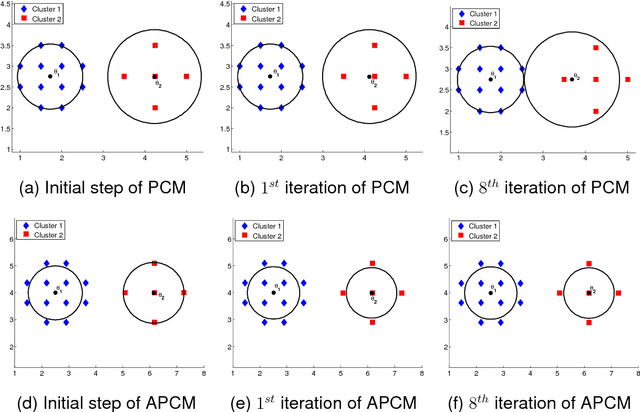
In this paper a novel possibilistic c-means clustering algorithm, called Adaptive Possibilistic c-means, is presented. Its main feature is that {\it all} its parameters, after their initialization, are properly adapted during its execution. Provided that the algorithm starts with a reasonable overestimate of the number of physical clusters formed by the data, it is capable, in principle, to unravel them (a long-standing issue in the clustering literature). This is due to the fully adaptive nature of the proposed algorithm that enables the removal of the clusters that gradually become obsolete. In addition, the adaptation of all its parameters increases the flexibility of the algorithm in following the variations in the formation of the clusters that occur from iteration to iteration. Theoretical results that are indicative of the convergence behavior of the algorithm are also provided. Finally, extensive simulation results on both synthetic and real data highlight the effectiveness of the proposed algorithm.

A variational Bayes framework for sparse adaptive estimation

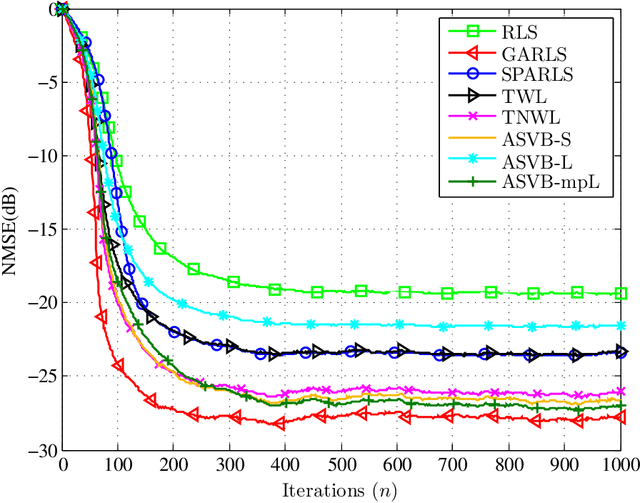
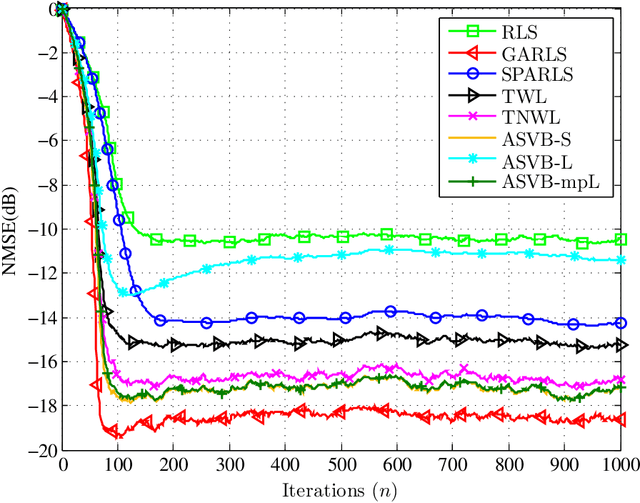
Recently, a number of mostly $\ell_1$-norm regularized least squares type deterministic algorithms have been proposed to address the problem of \emph{sparse} adaptive signal estimation and system identification. From a Bayesian perspective, this task is equivalent to maximum a posteriori probability estimation under a sparsity promoting heavy-tailed prior for the parameters of interest. Following a different approach, this paper develops a unifying framework of sparse \emph{variational Bayes} algorithms that employ heavy-tailed priors in conjugate hierarchical form to facilitate posterior inference. The resulting fully automated variational schemes are first presented in a batch iterative form. Then it is shown that by properly exploiting the structure of the batch estimation task, new sparse adaptive variational Bayes algorithms can be derived, which have the ability to impose and track sparsity during real-time processing in a time-varying environment. The most important feature of the proposed algorithms is that they completely eliminate the need for computationally costly parameter fine-tuning, a necessary ingredient of sparse adaptive deterministic algorithms. Extensive simulation results are provided to demonstrate the effectiveness of the new sparse variational Bayes algorithms against state-of-the-art deterministic techniques for adaptive channel estimation. The results show that the proposed algorithms are numerically robust and exhibit in general superior estimation performance compared to their deterministic counterparts.