Sparsity-aware Possibilistic Clustering Algorithms
Paper and Code
Oct 15, 2015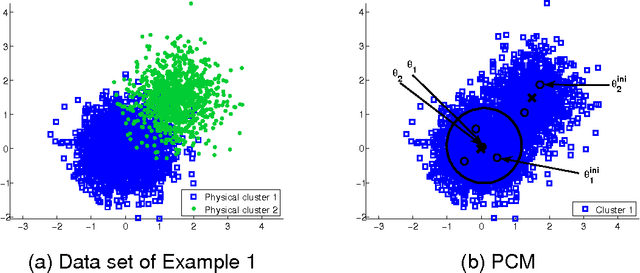
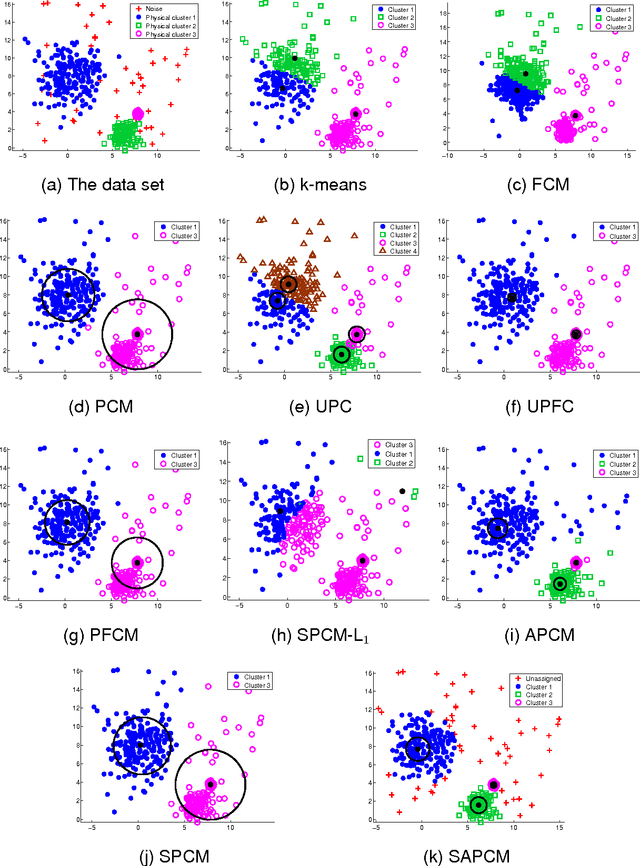
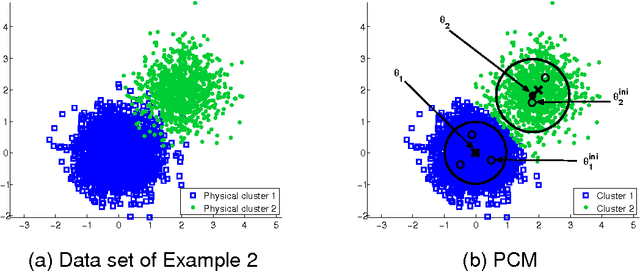
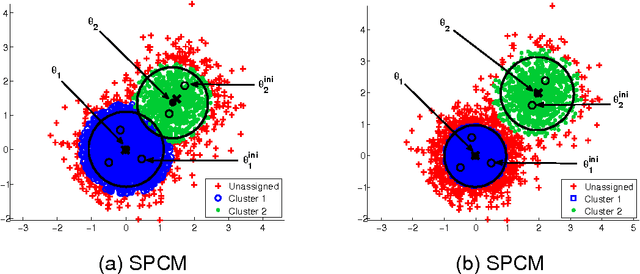
In this paper two novel possibilistic clustering algorithms are presented, which utilize the concept of sparsity. The first one, called sparse possibilistic c-means, exploits sparsity and can deal well with closely located clusters that may also be of significantly different densities. The second one, called sparse adaptive possibilistic c-means, is an extension of the first, where now the involved parameters are dynamically adapted. The latter can deal well with even more challenging cases, where, in addition to the above, clusters may be of significantly different variances. More specifically, it provides improved estimates of the cluster representatives, while, in addition, it has the ability to estimate the actual number of clusters, given an overestimate of it. Extensive experimental results on both synthetic and real data sets support the previous statements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge