A variational Bayes framework for sparse adaptive estimation
Paper and Code
Jan 13, 2014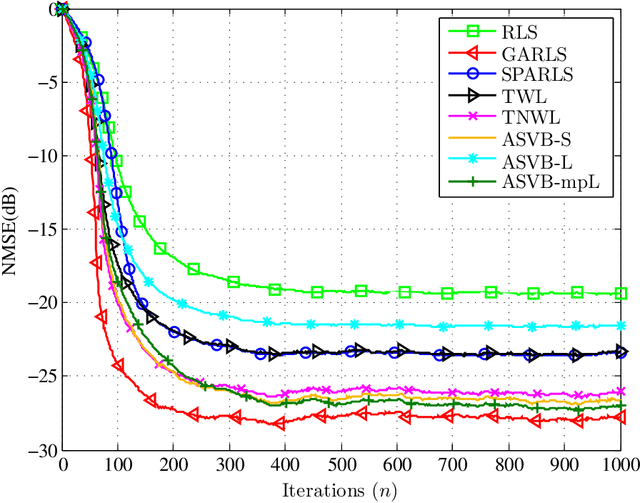

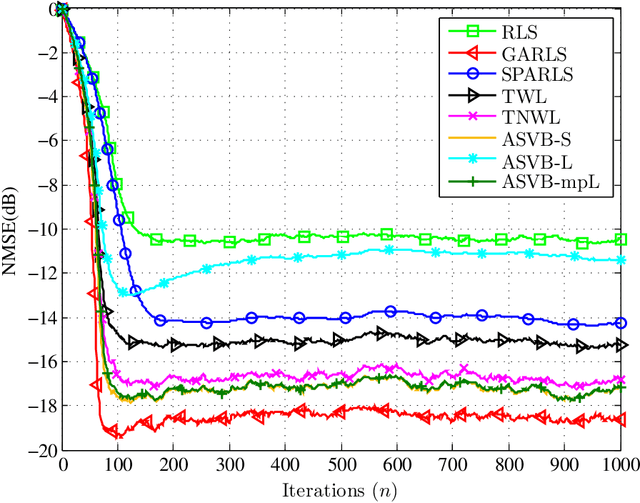

Recently, a number of mostly $\ell_1$-norm regularized least squares type deterministic algorithms have been proposed to address the problem of \emph{sparse} adaptive signal estimation and system identification. From a Bayesian perspective, this task is equivalent to maximum a posteriori probability estimation under a sparsity promoting heavy-tailed prior for the parameters of interest. Following a different approach, this paper develops a unifying framework of sparse \emph{variational Bayes} algorithms that employ heavy-tailed priors in conjugate hierarchical form to facilitate posterior inference. The resulting fully automated variational schemes are first presented in a batch iterative form. Then it is shown that by properly exploiting the structure of the batch estimation task, new sparse adaptive variational Bayes algorithms can be derived, which have the ability to impose and track sparsity during real-time processing in a time-varying environment. The most important feature of the proposed algorithms is that they completely eliminate the need for computationally costly parameter fine-tuning, a necessary ingredient of sparse adaptive deterministic algorithms. Extensive simulation results are provided to demonstrate the effectiveness of the new sparse variational Bayes algorithms against state-of-the-art deterministic techniques for adaptive channel estimation. The results show that the proposed algorithms are numerically robust and exhibit in general superior estimation performance compared to their deterministic counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge