A Novel Adaptive Possibilistic Clustering Algorithm
Paper and Code
Oct 15, 2015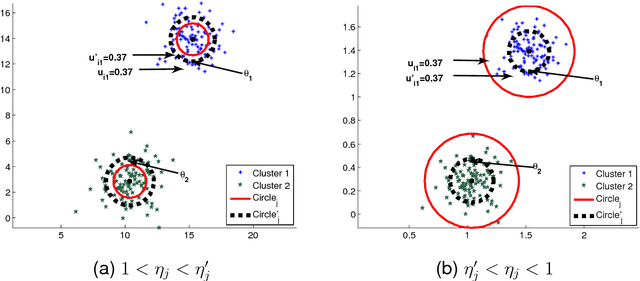
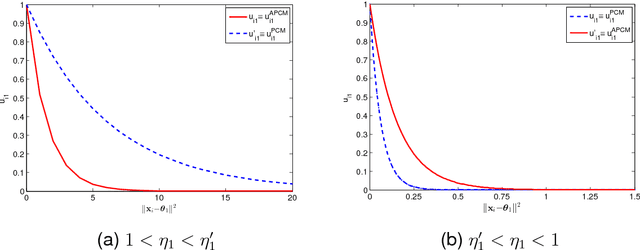
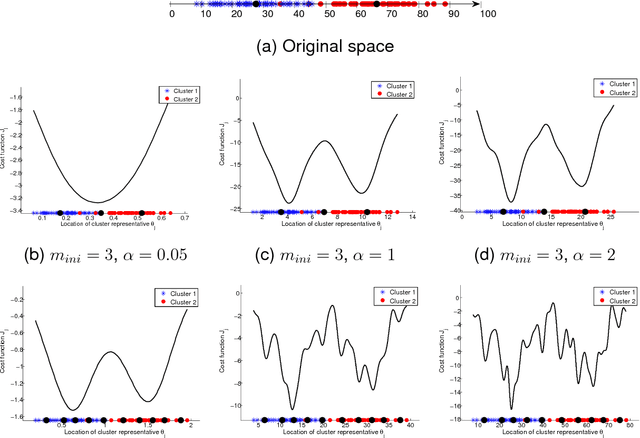
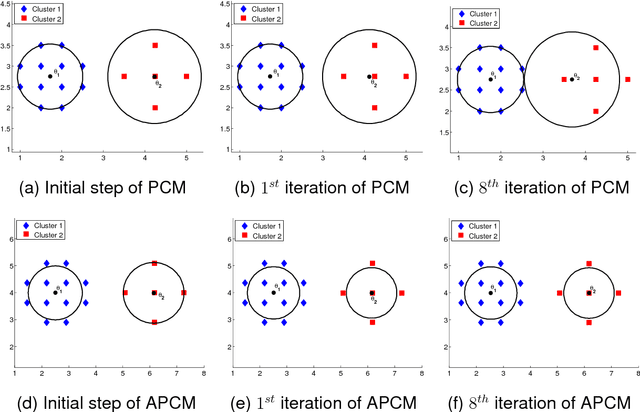
In this paper a novel possibilistic c-means clustering algorithm, called Adaptive Possibilistic c-means, is presented. Its main feature is that {\it all} its parameters, after their initialization, are properly adapted during its execution. Provided that the algorithm starts with a reasonable overestimate of the number of physical clusters formed by the data, it is capable, in principle, to unravel them (a long-standing issue in the clustering literature). This is due to the fully adaptive nature of the proposed algorithm that enables the removal of the clusters that gradually become obsolete. In addition, the adaptation of all its parameters increases the flexibility of the algorithm in following the variations in the formation of the clusters that occur from iteration to iteration. Theoretical results that are indicative of the convergence behavior of the algorithm are also provided. Finally, extensive simulation results on both synthetic and real data highlight the effectiveness of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge