Alternating Iteratively Reweighted Minimization Algorithms for Low-Rank Matrix Factorization
Paper and Code
Oct 05, 2017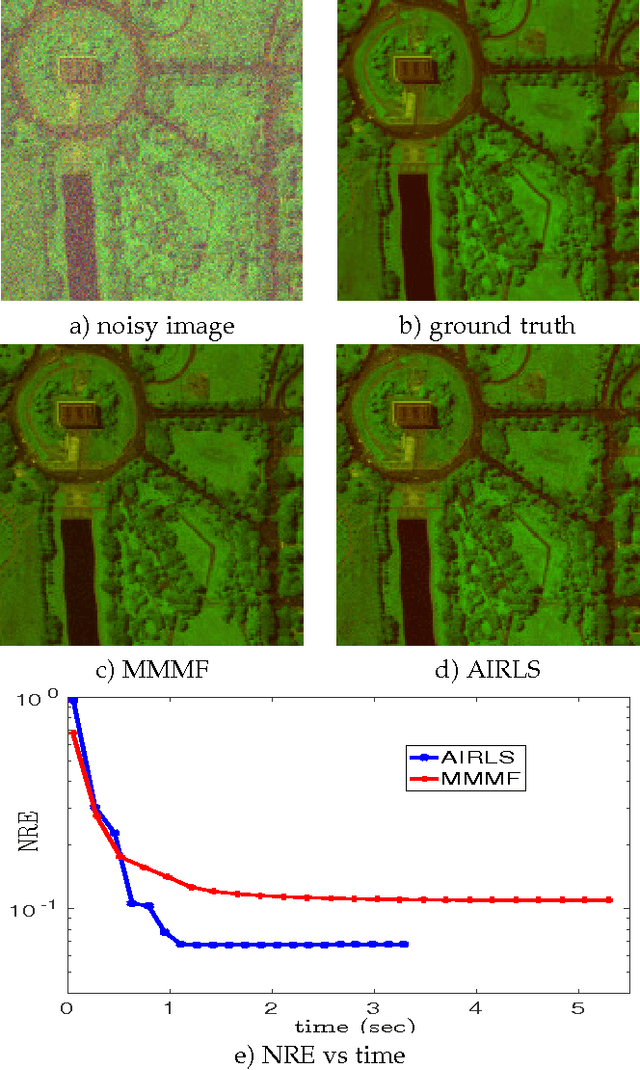
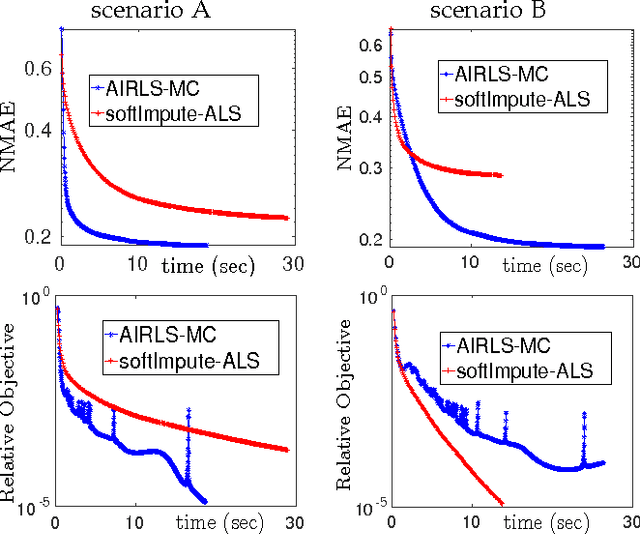
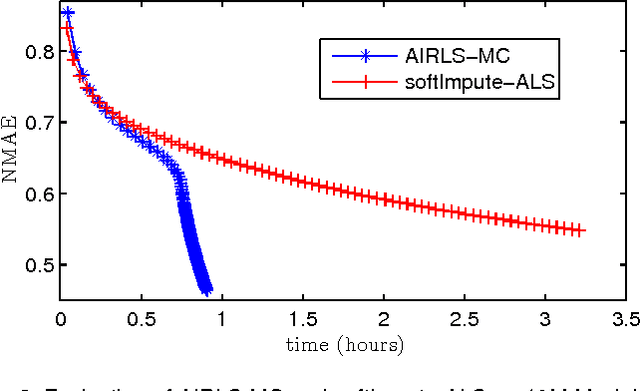
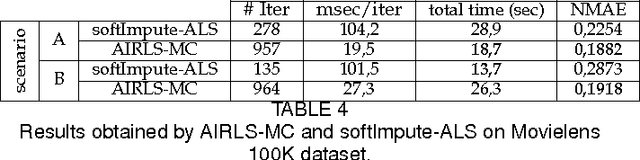
Nowadays, the availability of large-scale data in disparate application domains urges the deployment of sophisticated tools for extracting valuable knowledge out of this huge bulk of information. In that vein, low-rank representations (LRRs) which seek low-dimensional embeddings of data have naturally appeared. In an effort to reduce computational complexity and improve estimation performance, LRR has been viewed via a matrix factorization (MF) perspective. Recently, low-rank MF (LRMF) approaches have been proposed for tackling the inherent weakness of MF i.e., the unawareness of the dimension of the low-dimensional space where data reside. Herein, inspired by the merits of iterative reweighted schemes for rank minimization, we come up with a generic low-rank promoting regularization function. Then, focusing on a specific instance of it, we propose a regularizer that imposes column-sparsity jointly on the two matrix factors that result from MF, thus promoting low-rankness on the optimization problem. The problems of denoising, matrix completion and non-negative matrix factorization (NMF) are redefined according to the new LRMF formulation and solved via efficient Newton-type algorithms with proven theoretical guarantees as to their convergence and rates of convergence to stationary points. The effectiveness of the proposed algorithms is verified in diverse simulated and real data experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge