Online Low-Rank Subspace Learning from Incomplete Data: A Bayesian View
Paper and Code
Feb 12, 2016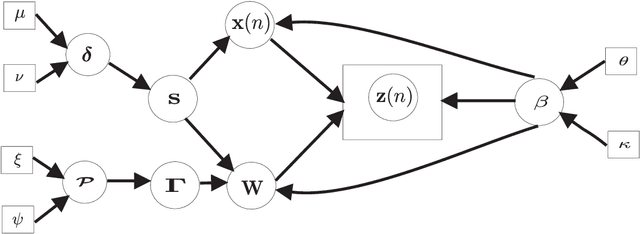
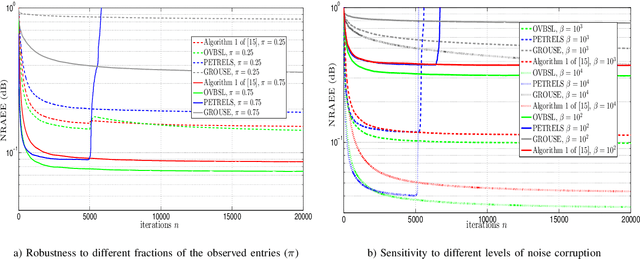
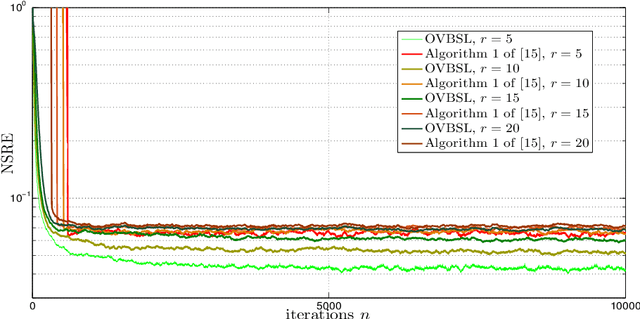
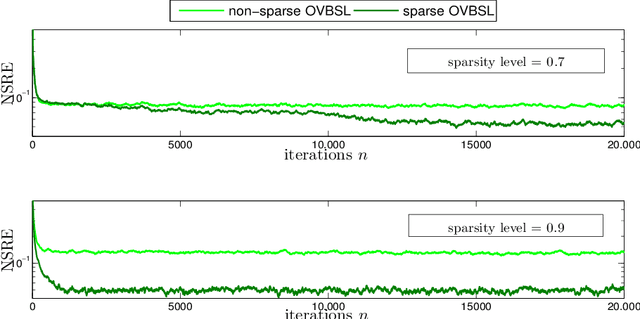
Extracting the underlying low-dimensional space where high-dimensional signals often reside has long been at the center of numerous algorithms in the signal processing and machine learning literature during the past few decades. At the same time, working with incomplete (partly observed) large scale datasets has recently been commonplace for diverse reasons. This so called {\it big data era} we are currently living calls for devising online subspace learning algorithms that can suitably handle incomplete data. Their envisaged objective is to {\it recursively} estimate the unknown subspace by processing streaming data sequentially, thus reducing computational complexity, while obviating the need for storing the whole dataset in memory. In this paper, an online variational Bayes subspace learning algorithm from partial observations is presented. To account for the unawareness of the true rank of the subspace, commonly met in practice, low-rankness is explicitly imposed on the sought subspace data matrix by exploiting sparse Bayesian learning principles. Moreover, sparsity, {\it simultaneously} to low-rankness, is favored on the subspace matrix by the sophisticated hierarchical Bayesian scheme that is adopted. In doing so, the proposed algorithm becomes adept in dealing with applications whereby the underlying subspace may be also sparse, as, e.g., in sparse dictionary learning problems. As shown, the new subspace tracking scheme outperforms its state-of-the-art counterparts in terms of estimation accuracy, in a variety of experiments conducted on simulated and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge