Penalizing Localized Dirichlet Energies in Low Rank Tensor Products

We study low-rank tensor-product B-spline (TPBS) models for regression tasks and investigate Dirichlet energy as a measure of smoothness. We show that TPBS models admit a closed-form expression for the Dirichlet energy, and reveal scenarios where perfect interpolation is possible with exponentially small Dirichlet energy. This renders global Dirichlet energy-based regularization ineffective. To address this limitation, we propose a novel regularization strategy based on local Dirichlet energies defined on small hypercubes centered at the training points. Leveraging pretrained TPBS models, we also introduce two estimators for inference from incomplete samples. Comparative experiments with neural networks demonstrate that TPBS models outperform neural networks in the overfitting regime for most datasets, and maintain competitive performance otherwise. Overall, TPBS models exhibit greater robustness to overfitting and consistently benefit from regularization, while neural networks are more sensitive to overfitting and less effective in leveraging regularization.

Revisiting Deep Generalized Canonical Correlation Analysis

Canonical correlation analysis (CCA) is a classic statistical method for discovering latent co-variation that underpins two or more observed random vectors. Several extensions and variations of CCA have been proposed that have strengthened our capabilities in terms of revealing common random factors from multiview datasets. In this work, we first revisit the most recent deterministic extensions of deep CCA and highlight the strengths and limitations of these state-of-the-art methods. Some methods allow trivial solutions, while others can miss weak common factors. Others overload the problem by also seeking to reveal what is not common among the views -- i.e., the private components that are needed to fully reconstruct each view. The latter tends to overload the problem and its computational and sample complexities. Aiming to improve upon these limitations, we design a novel and efficient formulation that alleviates some of the current restrictions. The main idea is to model the private components as conditionally independent given the common ones, which enables the proposed compact formulation. In addition, we also provide a sufficient condition for identifying the common random factors. Judicious experiments with synthetic and real datasets showcase the validity of our claims and the effectiveness of the proposed approach.

On High-dimensional and Low-rank Tensor Bandits

Most existing studies on linear bandits focus on the one-dimensional characterization of the overall system. While being representative, this formulation may fail to model applications with high-dimensional but favorable structures, such as the low-rank tensor representation for recommender systems. To address this limitation, this work studies a general tensor bandits model, where actions and system parameters are represented by tensors as opposed to vectors, and we particularly focus on the case that the unknown system tensor is low-rank. A novel bandit algorithm, coined TOFU (Tensor Optimism in the Face of Uncertainty), is developed. TOFU first leverages flexible tensor regression techniques to estimate low-dimensional subspaces associated with the system tensor. These estimates are then utilized to convert the original problem to a new one with norm constraints on its system parameters. Lastly, a norm-constrained bandit subroutine is adopted by TOFU, which utilizes these constraints to avoid exploring the entire high-dimensional parameter space. Theoretical analyses show that TOFU improves the best-known regret upper bound by a multiplicative factor that grows exponentially in the system order. A novel performance lower bound is also established, which further corroborates the efficiency of TOFU.

Finding the smallest or largest element of a tensor from its low-rank factors

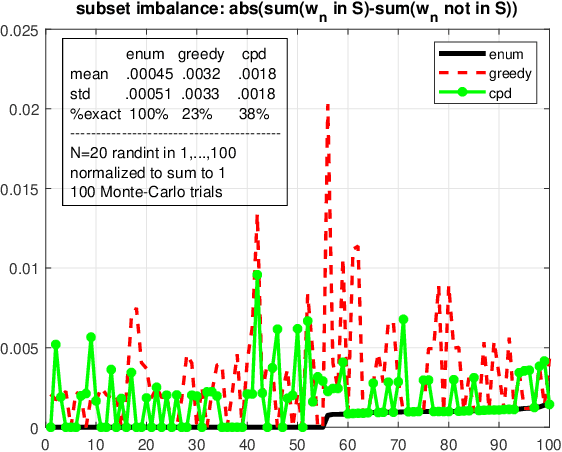
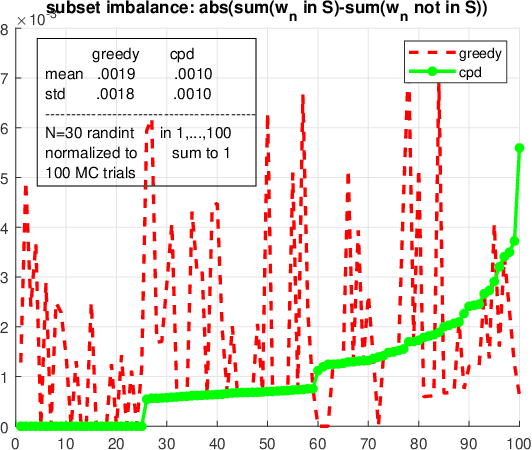
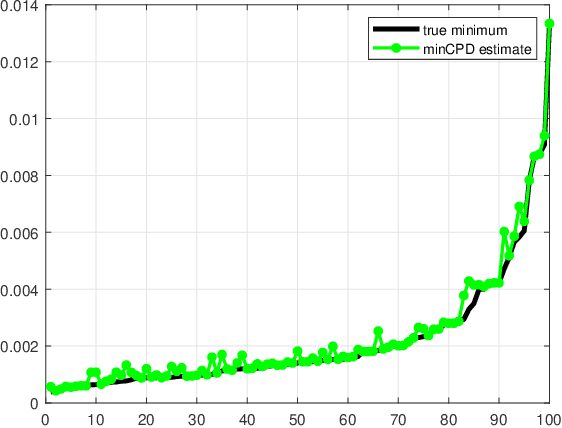
We consider the problem of finding the smallest or largest entry of a tensor of order $N$ that is specified via its rank decomposition. Stated in a different way, we are given $N$ sets of $R$-dimensional vectors and we wish to select one vector from each set such that the sum of the Hadamard product of the selected vectors is minimized or maximized. This is a fundamental tensor problem with numerous applications in embedding similarity search, recommender systems, graph mining, multivariate probability, and statistics. We show that this discrete optimization problem is NP-hard for any tensor rank higher than one, but also provide an equivalent continuous problem reformulation which is amenable to disciplined non-convex optimization. We propose a suite of gradient-based approximation algorithms whose performance in preliminary experiments appears to be promising.

Multisubject Task-Related fMRI Data Processing via a Two-Stage Generalized Canonical Correlation Analysis

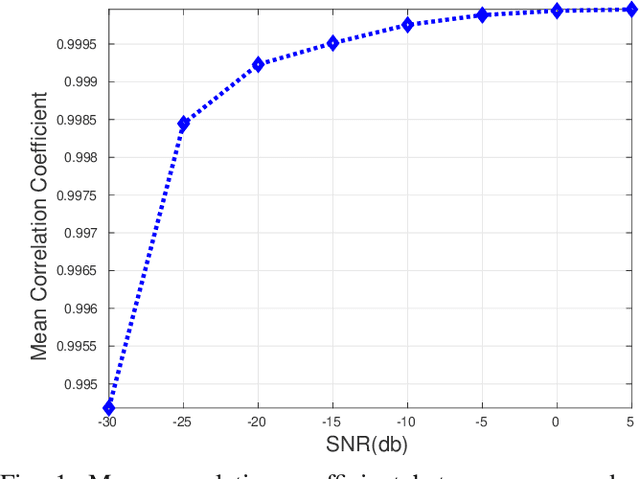
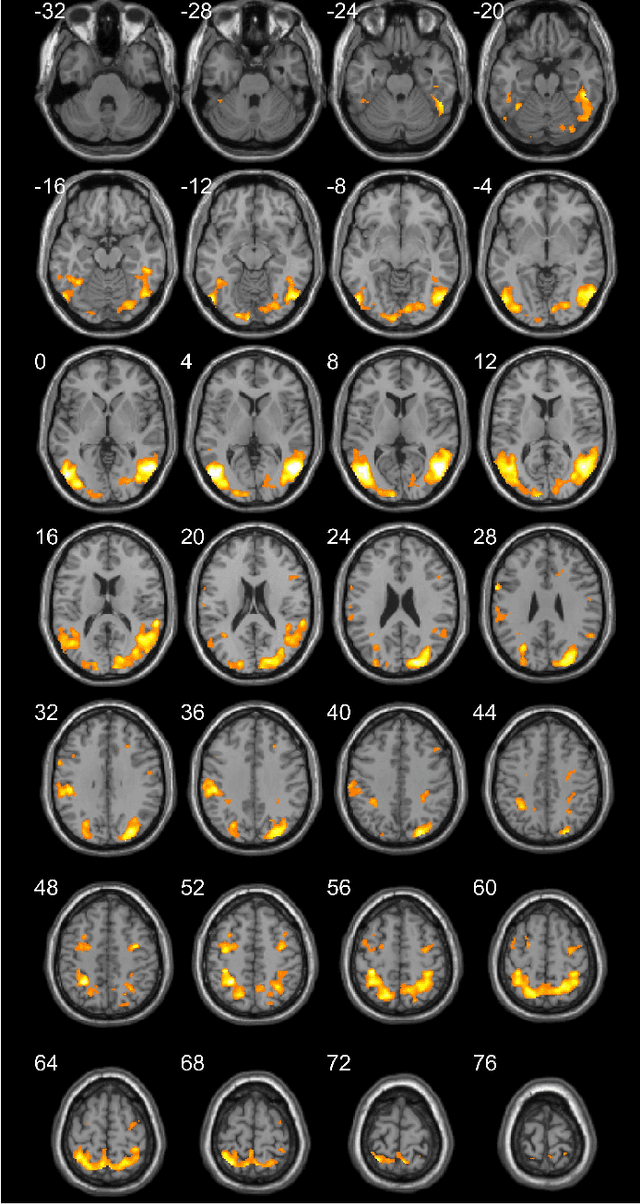
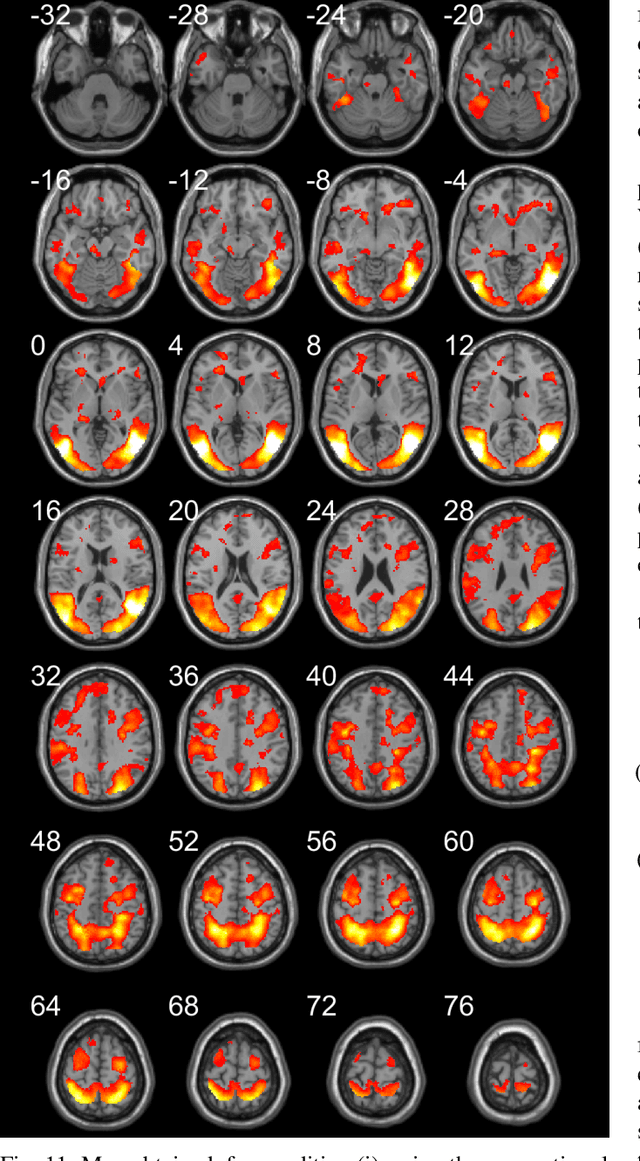
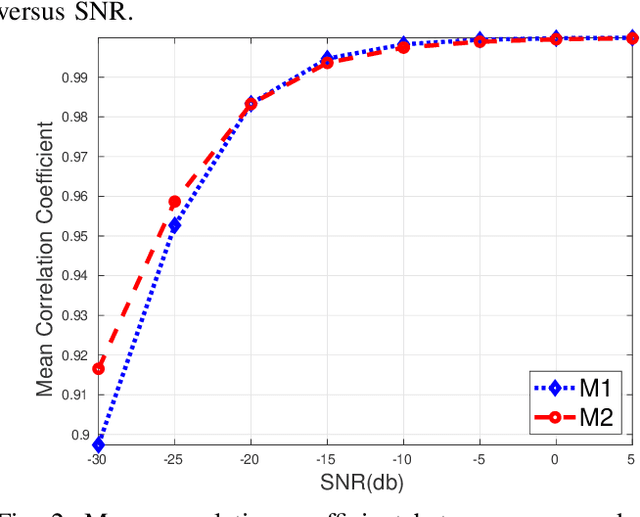
Functional magnetic resonance imaging (fMRI) is one of the most popular methods for studying the human brain. Task-related fMRI data processing aims to determine which brain areas are activated when a specific task is performed and is usually based on the Blood Oxygen Level Dependent (BOLD) signal. The background BOLD signal also reflects systematic fluctuations in regional brain activity which are attributed to the existence of resting-state brain networks. We propose a new fMRI data generating model which takes into consideration the existence of common task-related and resting-state components. We first estimate the common task-related temporal component, via two successive stages of generalized canonical correlation analysis and, then, we estimate the common task-related spatial component, leading to a task-related activation map. The experimental tests of our method with synthetic data reveal that we are able to obtain very accurate temporal and spatial estimates even at very low Signal to Noise Ratio (SNR), which is usually the case in fMRI data processing. The tests with real-world fMRI data show significant advantages over standard procedures based on General Linear Models (GLMs).

Learning Multivariate CDFs and Copulas using Tensor Factorization

Learning the multivariate distribution of data is a core challenge in statistics and machine learning. Traditional methods aim for the probability density function (PDF) and are limited by the curse of dimensionality. Modern neural methods are mostly based on black-box models, lacking identifiability guarantees. In this work, we aim to learn multivariate cumulative distribution functions (CDFs), as they can handle mixed random variables, allow efficient box probability evaluation, and have the potential to overcome local sample scarcity owing to their cumulative nature. We show that any grid sampled version of a joint CDF of mixed random variables admits a universal representation as a naive Bayes model via the Canonical Polyadic (tensor-rank) decomposition. By introducing a low-rank model, either directly in the raw data domain, or indirectly in a transformed (Copula) domain, the resulting model affords efficient sampling, closed form inference and uncertainty quantification, and comes with uniqueness guarantees under relatively mild conditions. We demonstrate the superior performance of the proposed model in several synthetic and real datasets and applications including regression, sampling and data imputation. Interestingly, our experiments with real data show that it is possible to obtain better density/mass estimates indirectly via a low-rank CDF model, than a low-rank PDF/PMF model.

Low-rank Characteristic Tensor Density Estimation Part II: Compression and Latent Density Estimation

Learning generative probabilistic models is a core problem in machine learning, which presents significant challenges due to the curse of dimensionality. This paper proposes a joint dimensionality reduction and non-parametric density estimation framework, using a novel estimator that can explicitly capture the underlying distribution of appropriate reduced-dimension representations of the input data. The idea is to jointly design a nonlinear dimensionality reducing auto-encoder to model the training data in terms of a parsimonious set of latent random variables, and learn a canonical low-rank tensor model of the joint distribution of the latent variables in the Fourier domain. The proposed latent density model is non-parametric and universal, as opposed to the predefined prior that is assumed in variational auto-encoders. Joint optimization of the auto-encoder and the latent density estimator is pursued via a formulation which learns both by minimizing a combination of the negative log-likelihood in the latent domain and the auto-encoder reconstruction loss. We demonstrate that the proposed model achieves very promising results on toy, tabular, and image datasets on regression tasks, sampling, and anomaly detection.

Probabilistic Simplex Component Analysis

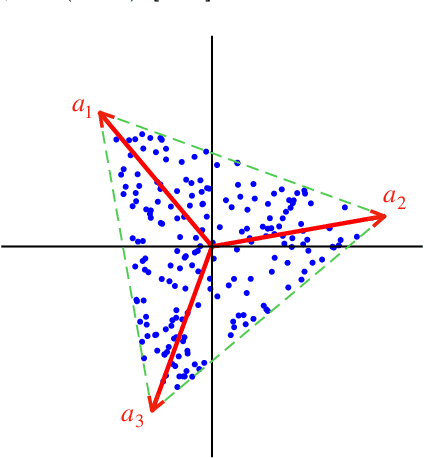
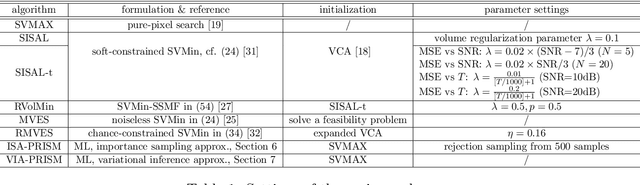
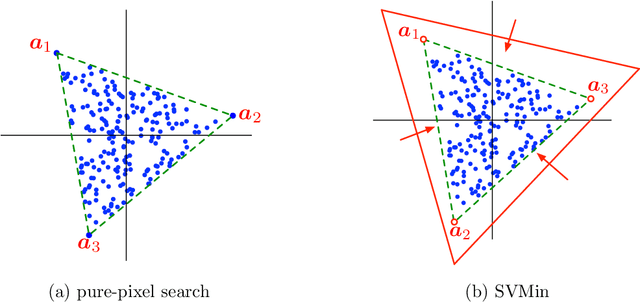
This study presents PRISM, a probabilistic simplex component analysis approach to identifying the vertices of a data-circumscribing simplex from data. The problem has a rich variety of applications, the most notable being hyperspectral unmixing in remote sensing and non-negative matrix factorization in machine learning. PRISM uses a simple probabilistic model, namely, uniform simplex data distribution and additive Gaussian noise, and it carries out inference by maximum likelihood. The inference model is sound in the sense that the vertices are provably identifiable under some assumptions, and it suggests that PRISM can be effective in combating noise when the number of data points is large. PRISM has strong, but hidden, relationships with simplex volume minimization, a powerful geometric approach for the same problem. We study these fundamental aspects, and we also consider algorithmic schemes based on importance sampling and variational inference. In particular, the variational inference scheme is shown to resemble a matrix factorization problem with a special regularizer, which draws an interesting connection to the matrix factorization approach. Numerical results are provided to demonstrate the potential of PRISM.

eTREE: Learning Tree-structured Embeddings

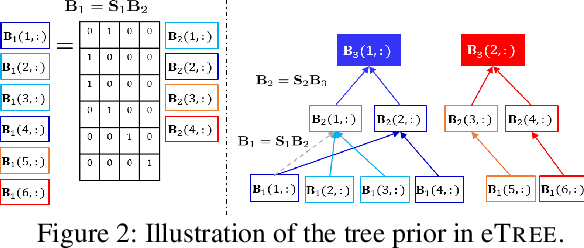
Matrix factorization (MF) plays an important role in a wide range of machine learning and data mining models. MF is commonly used to obtain item embeddings and feature representations due to its ability to capture correlations and higher-order statistical dependencies across dimensions. In many applications, the categories of items exhibit a hierarchical tree structure. For instance, human diseases can be divided into coarse categories, e.g., bacterial, and viral. These categories can be further divided into finer categories, e.g., viral infections can be respiratory, gastrointestinal, and exanthematous viral diseases. In e-commerce, products, movies, books, etc., are grouped into hierarchical categories, e.g., clothing items are divided by gender, then by type (formal, casual, etc.). While the tree structure and the categories of the different items may be known in some applications, they have to be learned together with the embeddings in many others. In this work, we propose eTREE, a model that incorporates the (usually ignored) tree structure to enhance the quality of the embeddings. We leverage the special uniqueness properties of Nonnegative MF (NMF) to prove identifiability of eTREE. The proposed model not only exploits the tree structure prior, but also learns the hierarchical clustering in an unsupervised data-driven fashion. We derive an efficient algorithmic solution and a scalable implementation of eTREE that exploits parallel computing, computation caching, and warm start strategies. We showcase the effectiveness of eTREE on real data from various application domains: healthcare, recommender systems, and education. We also demonstrate the meaningfulness of the tree obtained from eTREE by means of domain experts interpretation.

STELAR: Spatio-temporal Tensor Factorization with Latent Epidemiological Regularization

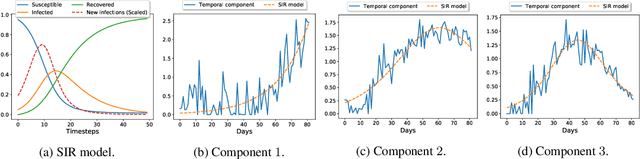
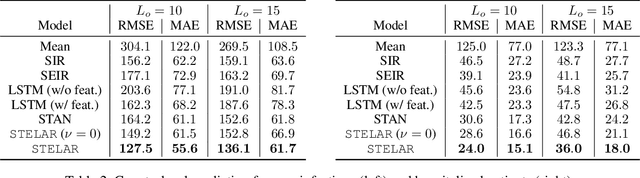
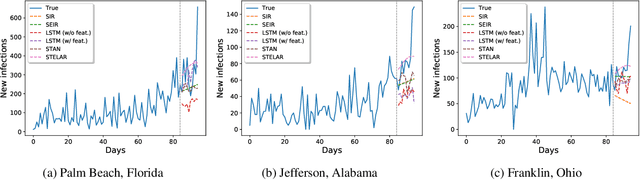
Accurate prediction of the transmission of epidemic diseases such as COVID-19 is crucial for implementing effective mitigation measures. In this work, we develop a tensor method to predict the evolution of epidemic trends for many regions simultaneously. We construct a 3-way spatio-temporal tensor (location, attribute, time) of case counts and propose a nonnegative tensor factorization with latent epidemiological model regularization named STELAR. Unlike standard tensor factorization methods which cannot predict slabs ahead, STELAR enables long-term prediction by incorporating latent temporal regularization through a system of discrete-time difference equations of a widely adopted epidemiological model. We use latent instead of location/attribute-level epidemiological dynamics to capture common epidemic profile sub-types and improve collaborative learning and prediction. We conduct experiments using both county- and state-level COVID-19 data and show that our model can identify interesting latent patterns of the epidemic. Finally, we evaluate the predictive ability of our method and show superior performance compared to the baselines, achieving up to 21% lower root mean square error and 25% lower mean absolute error for county-level prediction.