Magda Amiridi
Latent Temporal Flows for Multivariate Analysis of Wearables Data
Oct 14, 2022



Abstract:Increased use of sensor signals from wearable devices as rich sources of physiological data has sparked growing interest in developing health monitoring systems to identify changes in an individual's health profile. Indeed, machine learning models for sensor signals have enabled a diverse range of healthcare related applications including early detection of abnormalities, fertility tracking, and adverse drug effect prediction. However, these models can fail to account for the dependent high-dimensional nature of the underlying sensor signals. In this paper, we introduce Latent Temporal Flows, a method for multivariate time-series modeling tailored to this setting. We assume that a set of sequences is generated from a multivariate probabilistic model of an unobserved time-varying low-dimensional latent vector. Latent Temporal Flows simultaneously recovers a transformation of the observed sequences into lower-dimensional latent representations via deep autoencoder mappings, and estimates a temporally-conditioned probabilistic model via normalizing flows. Using data from the Apple Heart and Movement Study (AH&MS), we illustrate promising forecasting performance on these challenging signals. Additionally, by analyzing two and three dimensional representations learned by our model, we show that we can identify participants' $\text{VO}_2\text{max}$, a main indicator and summary of cardio-respiratory fitness, using only lower-level signals. Finally, we show that the proposed method consistently outperforms the state-of-the-art in multi-step forecasting benchmarks (achieving at least a $10\%$ performance improvement) on several real-world datasets, while enjoying increased computational efficiency.
Learning Multivariate CDFs and Copulas using Tensor Factorization
Oct 13, 2022



Abstract:Learning the multivariate distribution of data is a core challenge in statistics and machine learning. Traditional methods aim for the probability density function (PDF) and are limited by the curse of dimensionality. Modern neural methods are mostly based on black-box models, lacking identifiability guarantees. In this work, we aim to learn multivariate cumulative distribution functions (CDFs), as they can handle mixed random variables, allow efficient box probability evaluation, and have the potential to overcome local sample scarcity owing to their cumulative nature. We show that any grid sampled version of a joint CDF of mixed random variables admits a universal representation as a naive Bayes model via the Canonical Polyadic (tensor-rank) decomposition. By introducing a low-rank model, either directly in the raw data domain, or indirectly in a transformed (Copula) domain, the resulting model affords efficient sampling, closed form inference and uncertainty quantification, and comes with uniqueness guarantees under relatively mild conditions. We demonstrate the superior performance of the proposed model in several synthetic and real datasets and applications including regression, sampling and data imputation. Interestingly, our experiments with real data show that it is possible to obtain better density/mass estimates indirectly via a low-rank CDF model, than a low-rank PDF/PMF model.
Low-rank Characteristic Tensor Density Estimation Part II: Compression and Latent Density Estimation
Jun 20, 2021



Abstract:Learning generative probabilistic models is a core problem in machine learning, which presents significant challenges due to the curse of dimensionality. This paper proposes a joint dimensionality reduction and non-parametric density estimation framework, using a novel estimator that can explicitly capture the underlying distribution of appropriate reduced-dimension representations of the input data. The idea is to jointly design a nonlinear dimensionality reducing auto-encoder to model the training data in terms of a parsimonious set of latent random variables, and learn a canonical low-rank tensor model of the joint distribution of the latent variables in the Fourier domain. The proposed latent density model is non-parametric and universal, as opposed to the predefined prior that is assumed in variational auto-encoders. Joint optimization of the auto-encoder and the latent density estimator is pursued via a formulation which learns both by minimizing a combination of the negative log-likelihood in the latent domain and the auto-encoder reconstruction loss. We demonstrate that the proposed model achieves very promising results on toy, tabular, and image datasets on regression tasks, sampling, and anomaly detection.
Information-theoretic Feature Selection via Tensor Decomposition and Submodularity
Oct 30, 2020



Abstract:Feature selection by maximizing high-order mutual information between the selected feature vector and a target variable is the gold standard in terms of selecting the best subset of relevant features that maximizes the performance of prediction models. However, such an approach typically requires knowledge of the multivariate probability distribution of all features and the target, and involves a challenging combinatorial optimization problem. Recent work has shown that any joint Probability Mass Function (PMF) can be represented as a naive Bayes model, via Canonical Polyadic (tensor rank) Decomposition. In this paper, we introduce a low-rank tensor model of the joint PMF of all variables and indirect targeting as a way of mitigating complexity and maximizing the classification performance for a given number of features. Through low-rank modeling of the joint PMF, it is possible to circumvent the curse of dimensionality by learning principal components of the joint distribution. By indirectly aiming to predict the latent variable of the naive Bayes model instead of the original target variable, it is possible to formulate the feature selection problem as maximization of a monotone submodular function subject to a cardinality constraint - which can be tackled using a greedy algorithm that comes with performance guarantees. Numerical experiments with several standard datasets suggest that the proposed approach compares favorably to the state-of-art for this important problem.
Nonparametric Multivariate Density Estimation: A Low-Rank Characteristic Function Approach
Aug 27, 2020



Abstract:Effective non-parametric density estimation is a key challenge in high-dimensional multivariate data analysis. In this paper,we propose a novel approach that builds upon tensor factorization tools. Any multivariate density can be represented by its characteristic function, via the Fourier transform. If the sought density is compactly supported, then its characteristic function can be approximated, within controllable error, by a finite tensor of leading Fourier coefficients, whose size de-pends on the smoothness of the underlying density. This tensor can be naturally estimated from observed realizations of the random vector of interest, via sample averaging. In order to circumvent the curse of dimensionality, we introduce a low-rank model of this characteristic tensor, which significantly improves the density estimate especially for high-dimensional data and/or in the sample-starved regime. By virtue of uniqueness of low-rank tensor decomposition, under certain conditions, our method enables learning the true data-generating distribution. We demonstrate the very promising performance of the proposed method using several measured datasets.
From Gene Expression to Drug Response: A Collaborative Filtering Approach
Oct 31, 2018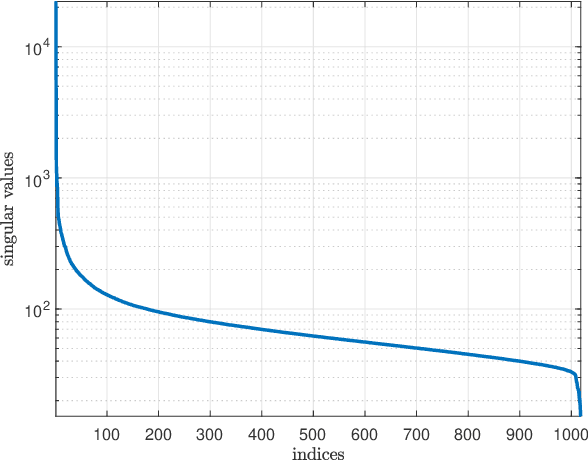
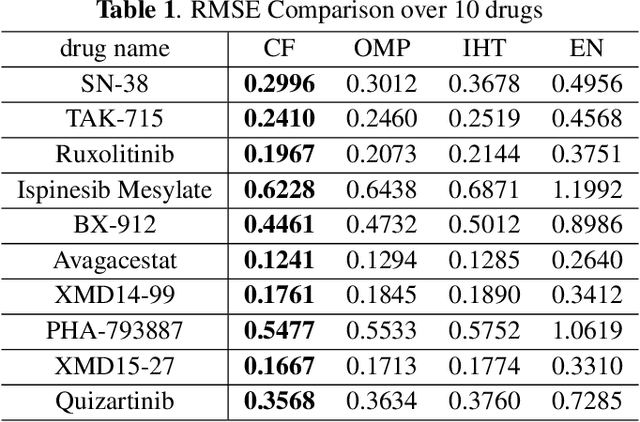
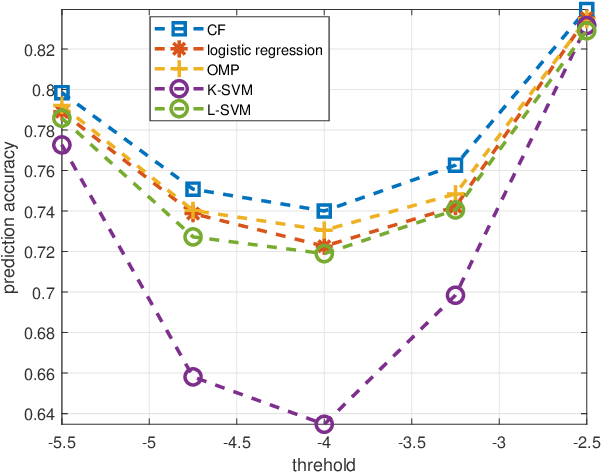
Abstract:Predicting the response of cancer cells to drugs is an important problem in pharmacogenomics. Recent efforts in generation of large scale datasets profiling gene expression and drug sensitivity in cell lines have provided a unique opportunity to study this problem. However, one major challenge is the small number of samples (cell lines) compared to the number of features (genes) even in these large datasets. We propose a collaborative filtering (CF) like algorithm for modeling gene-drug relationship to identify patients most likely to benefit from a treatment. Due to the correlation of gene expressions in different cell lines, the gene expression matrix is approximately low-rank, which suggests that drug responses could be estimated from a reduced dimension latent space of the gene expression. Towards this end, we propose a joint low-rank matrix factorization and latent linear regression approach. Experiments with data from the Genomics of Drug Sensitivity in Cancer database are included to show that the proposed method can predict drug-gene associations better than the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge