Analysis and Utilization of Entrainment on Acoustic and Emotion Features in User-agent Dialogue

Entrainment is the phenomenon by which an interlocutor adapts their speaking style to align with their partner in conversations. It has been found in different dimensions as acoustic, prosodic, lexical or syntactic. In this work, we explore and utilize the entrainment phenomenon to improve spoken dialogue systems for voice assistants. We first examine the existence of the entrainment phenomenon in human-to-human dialogues in respect to acoustic feature and then extend the analysis to emotion features. The analysis results show strong evidence of entrainment in terms of both acoustic and emotion features. Based on this findings, we implement two entrainment policies and assess if the integration of entrainment principle into a Text-to-Speech (TTS) system improves the synthesis performance and the user experience. It is found that the integration of the entrainment principle into a TTS system brings performance improvement when considering acoustic features, while no obvious improvement is observed when considering emotion features.

Low-rank Characteristic Tensor Density Estimation Part II: Compression and Latent Density Estimation

Learning generative probabilistic models is a core problem in machine learning, which presents significant challenges due to the curse of dimensionality. This paper proposes a joint dimensionality reduction and non-parametric density estimation framework, using a novel estimator that can explicitly capture the underlying distribution of appropriate reduced-dimension representations of the input data. The idea is to jointly design a nonlinear dimensionality reducing auto-encoder to model the training data in terms of a parsimonious set of latent random variables, and learn a canonical low-rank tensor model of the joint distribution of the latent variables in the Fourier domain. The proposed latent density model is non-parametric and universal, as opposed to the predefined prior that is assumed in variational auto-encoders. Joint optimization of the auto-encoder and the latent density estimator is pursued via a formulation which learns both by minimizing a combination of the negative log-likelihood in the latent domain and the auto-encoder reconstruction loss. We demonstrate that the proposed model achieves very promising results on toy, tabular, and image datasets on regression tasks, sampling, and anomaly detection.

Multi-version Tensor Completion for Time-delayed Spatio-temporal Data

Real-world spatio-temporal data is often incomplete or inaccurate due to various data loading delays. For example, a location-disease-time tensor of case counts can have multiple delayed updates of recent temporal slices for some locations or diseases. Recovering such missing or noisy (under-reported) elements of the input tensor can be viewed as a generalized tensor completion problem. Existing tensor completion methods usually assume that i) missing elements are randomly distributed and ii) noise for each tensor element is i.i.d. zero-mean. Both assumptions can be violated for spatio-temporal tensor data. We often observe multiple versions of the input tensor with different under-reporting noise levels. The amount of noise can be time- or location-dependent as more updates are progressively introduced to the tensor. We model such dynamic data as a multi-version tensor with an extra tensor mode capturing the data updates. We propose a low-rank tensor model to predict the updates over time. We demonstrate that our method can accurately predict the ground-truth values of many real-world tensors. We obtain up to 27.2% lower root mean-squared-error compared to the best baseline method. Finally, we extend our method to track the tensor data over time, leading to significant computational savings.

STELAR: Spatio-temporal Tensor Factorization with Latent Epidemiological Regularization

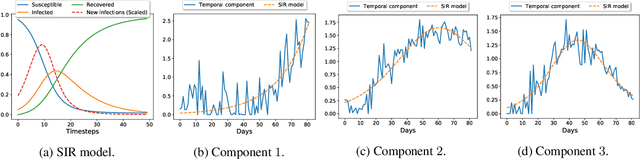
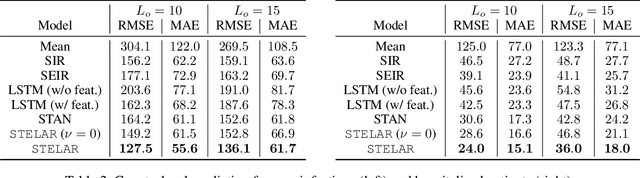
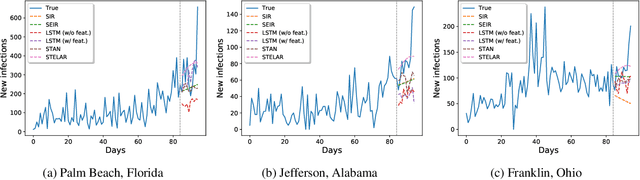
Accurate prediction of the transmission of epidemic diseases such as COVID-19 is crucial for implementing effective mitigation measures. In this work, we develop a tensor method to predict the evolution of epidemic trends for many regions simultaneously. We construct a 3-way spatio-temporal tensor (location, attribute, time) of case counts and propose a nonnegative tensor factorization with latent epidemiological model regularization named STELAR. Unlike standard tensor factorization methods which cannot predict slabs ahead, STELAR enables long-term prediction by incorporating latent temporal regularization through a system of discrete-time difference equations of a widely adopted epidemiological model. We use latent instead of location/attribute-level epidemiological dynamics to capture common epidemic profile sub-types and improve collaborative learning and prediction. We conduct experiments using both county- and state-level COVID-19 data and show that our model can identify interesting latent patterns of the epidemic. Finally, we evaluate the predictive ability of our method and show superior performance compared to the baselines, achieving up to 21% lower root mean square error and 25% lower mean absolute error for county-level prediction.

Information-theoretic Feature Selection via Tensor Decomposition and Submodularity

Feature selection by maximizing high-order mutual information between the selected feature vector and a target variable is the gold standard in terms of selecting the best subset of relevant features that maximizes the performance of prediction models. However, such an approach typically requires knowledge of the multivariate probability distribution of all features and the target, and involves a challenging combinatorial optimization problem. Recent work has shown that any joint Probability Mass Function (PMF) can be represented as a naive Bayes model, via Canonical Polyadic (tensor rank) Decomposition. In this paper, we introduce a low-rank tensor model of the joint PMF of all variables and indirect targeting as a way of mitigating complexity and maximizing the classification performance for a given number of features. Through low-rank modeling of the joint PMF, it is possible to circumvent the curse of dimensionality by learning principal components of the joint distribution. By indirectly aiming to predict the latent variable of the naive Bayes model instead of the original target variable, it is possible to formulate the feature selection problem as maximization of a monotone submodular function subject to a cardinality constraint - which can be tackled using a greedy algorithm that comes with performance guarantees. Numerical experiments with several standard datasets suggest that the proposed approach compares favorably to the state-of-art for this important problem.

Nonparametric Multivariate Density Estimation: A Low-Rank Characteristic Function Approach

Effective non-parametric density estimation is a key challenge in high-dimensional multivariate data analysis. In this paper,we propose a novel approach that builds upon tensor factorization tools. Any multivariate density can be represented by its characteristic function, via the Fourier transform. If the sought density is compactly supported, then its characteristic function can be approximated, within controllable error, by a finite tensor of leading Fourier coefficients, whose size de-pends on the smoothness of the underlying density. This tensor can be naturally estimated from observed realizations of the random vector of interest, via sample averaging. In order to circumvent the curse of dimensionality, we introduce a low-rank model of this characteristic tensor, which significantly improves the density estimate especially for high-dimensional data and/or in the sample-starved regime. By virtue of uniqueness of low-rank tensor decomposition, under certain conditions, our method enables learning the true data-generating distribution. We demonstrate the very promising performance of the proposed method using several measured datasets.

Crowdsourcing via Pairwise Co-occurrences: Identifiability and Algorithms

The data deluge comes with high demands for data labeling. Crowdsourcing (or, more generally, ensemble learning) techniques aim to produce accurate labels via integrating noisy, non-expert labeling from annotators. The classic Dawid-Skene estimator and its accompanying expectation maximization (EM) algorithm have been widely used, but the theoretical properties are not fully understood. Tensor methods were proposed to guarantee identification of the Dawid-Skene model, but the sample complexity is a hurdle for applying such approaches---since the tensor methods hinge on the availability of third-order statistics that are hard to reliably estimate given limited data. In this paper, we propose a framework using pairwise co-occurrences of the annotator responses, which naturally admits lower sample complexity. We show that the approach can identify the Dawid-Skene model under realistic conditions. We propose an algebraic algorithm reminiscent of convex geometry-based structured matrix factorization to solve the model identification problem efficiently, and an identifiability-enhanced algorithm for handling more challenging and critical scenarios. Experiments show that the proposed algorithms outperform the state-of-art algorithms under a variety of scenarios.

Learning Mixtures of Smooth Product Distributions: Identifiability and Algorithm

We study the problem of learning a mixture model of non-parametric product distributions. The problem of learning a mixture model is that of finding the component distributions along with the mixing weights using observed samples generated from the mixture. The problem is well-studied in the parametric setting, i.e., when the component distributions are members of a parametric family -- such as Gaussian distributions. In this work, we focus on multivariate mixtures of non-parametric product distributions and propose a two-stage approach which recovers the component distributions of the mixture under a smoothness condition. Our approach builds upon the identifiability properties of the canonical polyadic (low-rank) decomposition of tensors, in tandem with Fourier and Shannon-Nyquist sampling staples from signal processing. We demonstrate the effectiveness of the approach on synthetic and real datasets.

Tensors, Learning, and 'Kolmogorov Extension' for Finite-alphabet Random Vectors

Estimating the joint probability mass function (PMF) of a set of random variables lies at the heart of statistical learning and signal processing. Without structural assumptions, such as modeling the variables as a Markov chain, tree, or other graphical model, joint PMF estimation is often considered mission impossible - the number of unknowns grows exponentially with the number of variables. But who gives us the structural model? Is there a generic, `non-parametric' way to control joint PMF complexity without relying on a priori structural assumptions regarding the underlying probability model? Is it possible to discover the operational structure without biasing the analysis up front? What if we only observe random subsets of the variables, can we still reliably estimate the joint PMF of all? This paper shows, perhaps surprisingly, that if the joint PMF of any three variables can be estimated, then the joint PMF of all the variables can be provably recovered under relatively mild conditions. The result is reminiscent of Kolmogorov's extension theorem - consistent specification of lower-dimensional distributions induces a unique probability measure for the entire process. The difference is that for processes of limited complexity (rank of the high-dimensional PMF) it is possible to obtain complete characterization from only three-dimensional distributions. In fact not all three-dimensional PMFs are needed; and under more stringent conditions even two-dimensional will do. Exploiting multilinear algebra, this paper proves that such higher-dimensional PMF completion can be guaranteed - several pertinent identifiability results are derived. It also provides a practical and efficient algorithm to carry out the recovery task. Judiciously designed simulations and real-data experiments on movie recommendation and data classification are presented to showcase the effectiveness of the approach.

Completing a joint PMF from projections: a low-rank coupled tensor factorization approach

There has recently been considerable interest in completing a low-rank matrix or tensor given only a small fraction (or few linear combinations) of its entries. Related approaches have found considerable success in the area of recommender systems, under machine learning. From a statistical estimation point of view, the gold standard is to have access to the joint probability distribution of all pertinent random variables, from which any desired optimal estimator can be readily derived. In practice high-dimensional joint distributions are very hard to estimate, and only estimates of low-dimensional projections may be available. We show that it is possible to identify higher-order joint PMFs from lower-order marginalized PMFs using coupled low-rank tensor factorization. Our approach features guaranteed identifiability when the full joint PMF is of low-enough rank, and effective approximation otherwise. We provide an algorithmic approach to compute the sought factors, and illustrate the merits of our approach using rating prediction as an example.