Multisubject Task-Related fMRI Data Processing via a Two-Stage Generalized Canonical Correlation Analysis

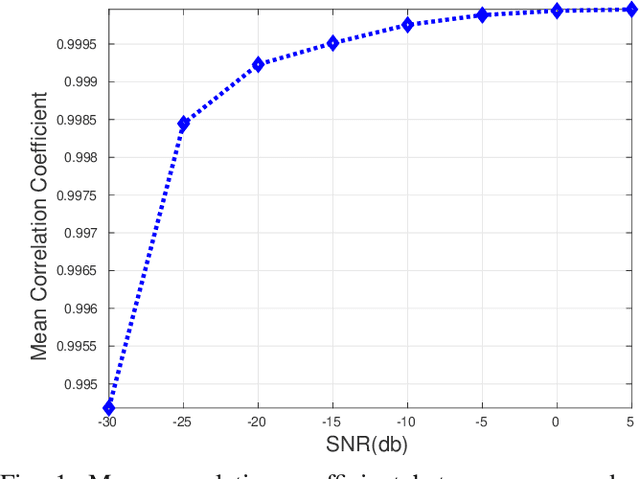
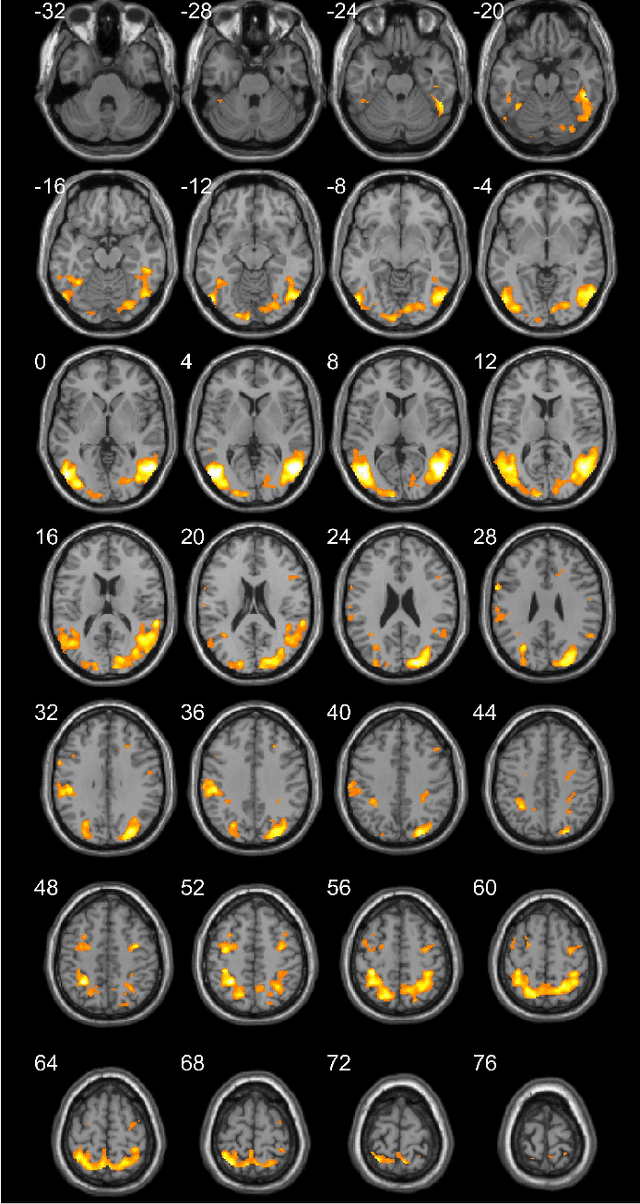
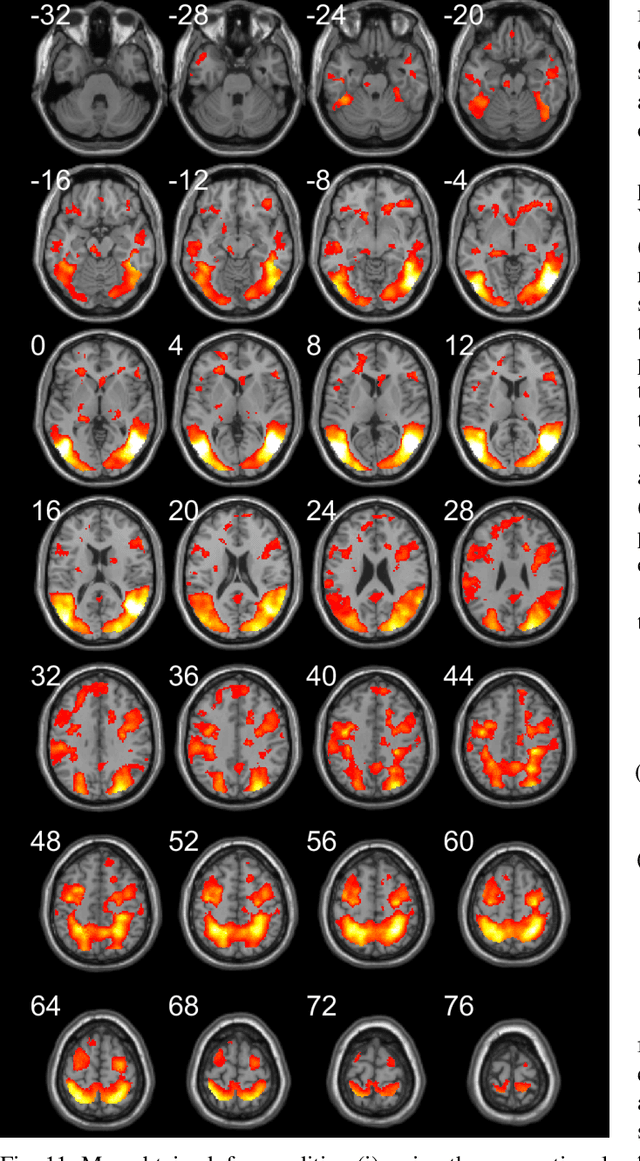
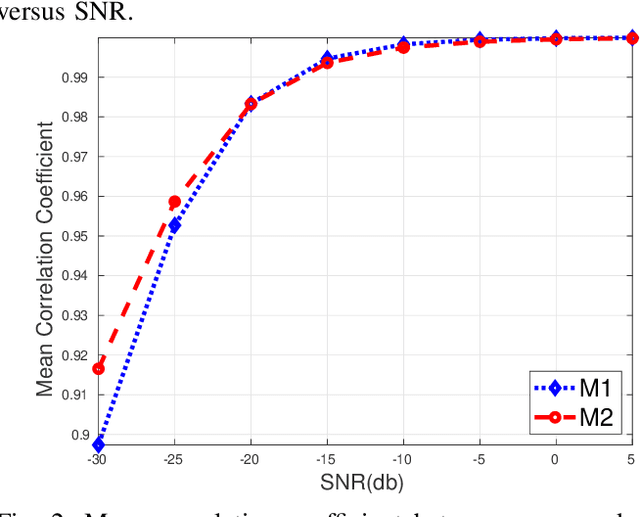
Functional magnetic resonance imaging (fMRI) is one of the most popular methods for studying the human brain. Task-related fMRI data processing aims to determine which brain areas are activated when a specific task is performed and is usually based on the Blood Oxygen Level Dependent (BOLD) signal. The background BOLD signal also reflects systematic fluctuations in regional brain activity which are attributed to the existence of resting-state brain networks. We propose a new fMRI data generating model which takes into consideration the existence of common task-related and resting-state components. We first estimate the common task-related temporal component, via two successive stages of generalized canonical correlation analysis and, then, we estimate the common task-related spatial component, leading to a task-related activation map. The experimental tests of our method with synthetic data reveal that we are able to obtain very accurate temporal and spatial estimates even at very low Signal to Noise Ratio (SNR), which is usually the case in fMRI data processing. The tests with real-world fMRI data show significant advantages over standard procedures based on General Linear Models (GLMs).

An Accelerated Stochastic Gradient for Canonical Polyadic Decomposition

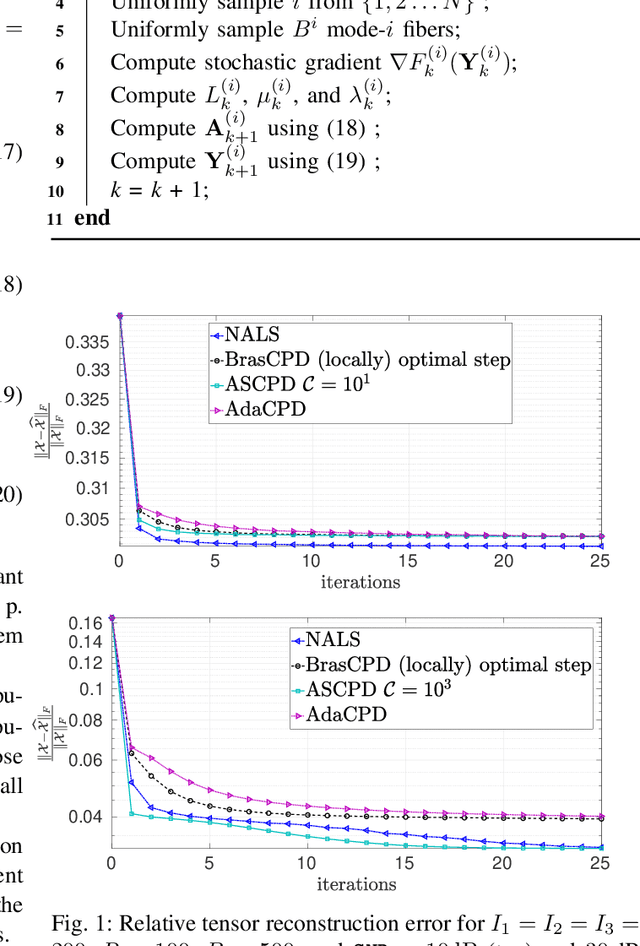
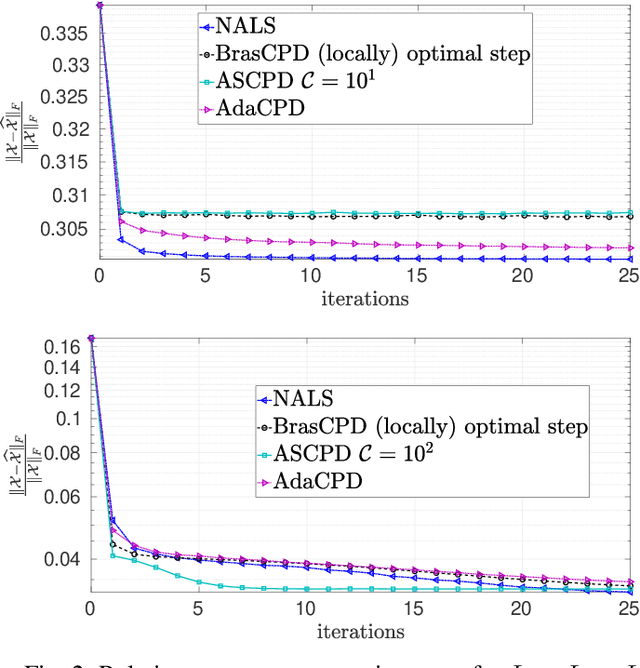
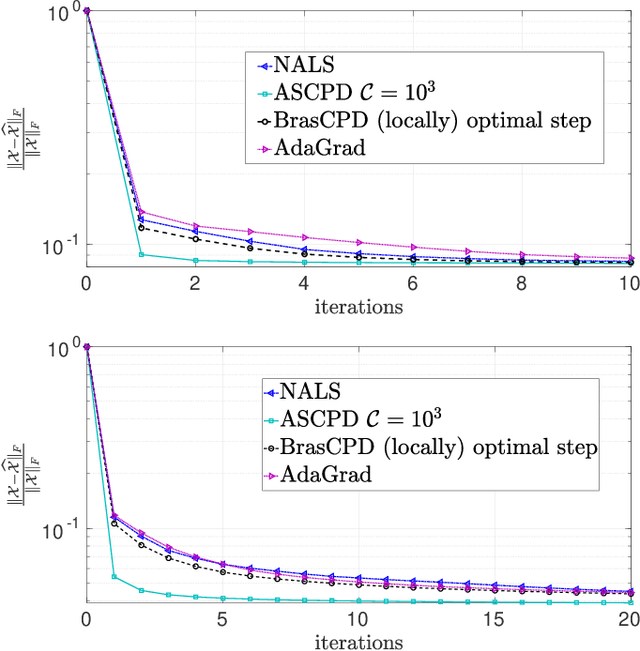
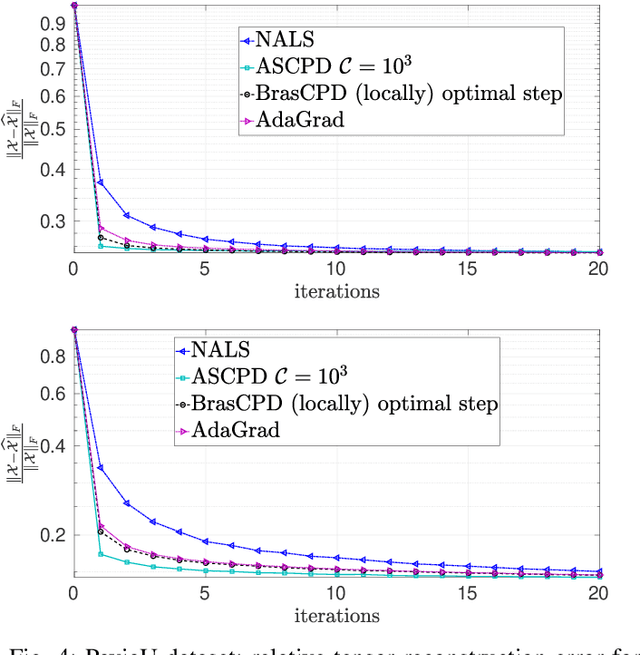
We consider the problem of structured canonical polyadic decomposition. If the size of the problem is very big, then stochastic gradient approaches are viable alternatives to classical methods, such as Alternating Optimization and All-At-Once optimization. We extend a recent stochastic gradient approach by employing an acceleration step (Nesterov momentum) in each iteration. We compare our approach with state-of-the-art alternatives, using both synthetic and real-world data, and find it to be very competitive.

Accelerated Stochastic Gradient for Nonnegative Tensor Completion and Parallel Implementation

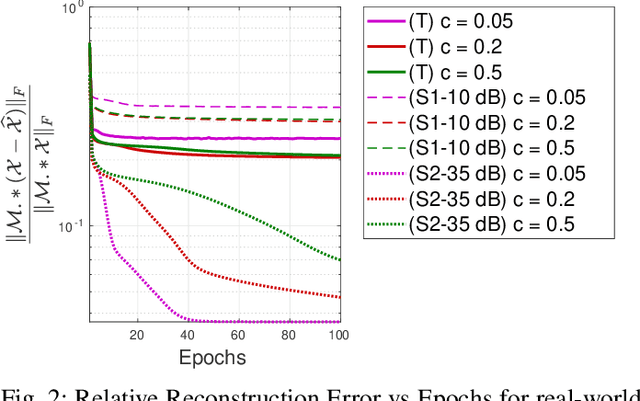
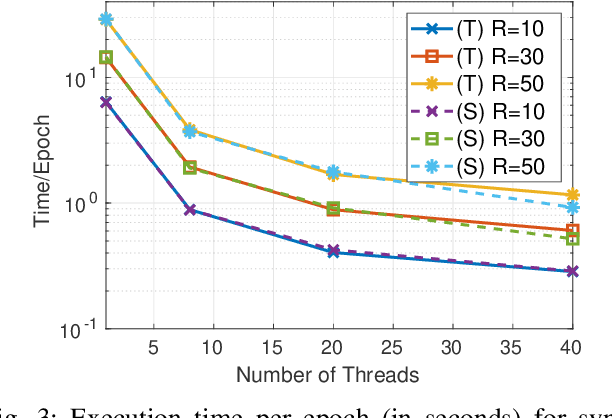
We consider the problem of nonnegative tensor completion. We adopt the alternating optimization framework and solve each nonnegative matrix completion problem via a stochastic variation of the accelerated gradient algorithm. We experimentally test the effectiveness and the efficiency of our algorithm using both real-world and synthetic data. We develop a shared-memory implementation of our algorithm using the multi-threaded API OpenMP, which attains significant speedup. We believe that our approach is a very competitive candidate for the solution of very large nonnegative tensor completion problems.

A Flexible and Efficient Algorithmic Framework for Constrained Matrix and Tensor Factorization

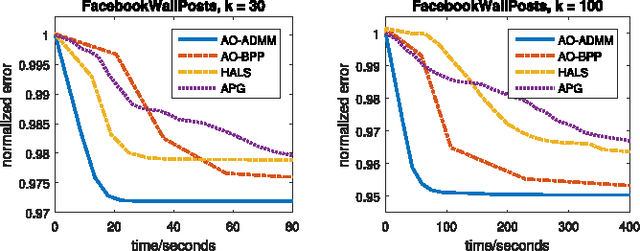
We propose a general algorithmic framework for constrained matrix and tensor factorization, which is widely used in signal processing and machine learning. The new framework is a hybrid between alternating optimization (AO) and the alternating direction method of multipliers (ADMM): each matrix factor is updated in turn, using ADMM, hence the name AO-ADMM. This combination can naturally accommodate a great variety of constraints on the factor matrices, and almost all possible loss measures for the fitting. Computation caching and warm start strategies are used to ensure that each update is evaluated efficiently, while the outer AO framework exploits recent developments in block coordinate descent (BCD)-type methods which help ensure that every limit point is a stationary point, as well as faster and more robust convergence in practice. Three special cases are studied in detail: non-negative matrix/tensor factorization, constrained matrix/tensor completion, and dictionary learning. Extensive simulations and experiments with real data are used to showcase the effectiveness and broad applicability of the proposed framework.