Penalizing Localized Dirichlet Energies in Low Rank Tensor Products

We study low-rank tensor-product B-spline (TPBS) models for regression tasks and investigate Dirichlet energy as a measure of smoothness. We show that TPBS models admit a closed-form expression for the Dirichlet energy, and reveal scenarios where perfect interpolation is possible with exponentially small Dirichlet energy. This renders global Dirichlet energy-based regularization ineffective. To address this limitation, we propose a novel regularization strategy based on local Dirichlet energies defined on small hypercubes centered at the training points. Leveraging pretrained TPBS models, we also introduce two estimators for inference from incomplete samples. Comparative experiments with neural networks demonstrate that TPBS models outperform neural networks in the overfitting regime for most datasets, and maintain competitive performance otherwise. Overall, TPBS models exhibit greater robustness to overfitting and consistently benefit from regularization, while neural networks are more sensitive to overfitting and less effective in leveraging regularization.

Revisiting Deep Generalized Canonical Correlation Analysis

Canonical correlation analysis (CCA) is a classic statistical method for discovering latent co-variation that underpins two or more observed random vectors. Several extensions and variations of CCA have been proposed that have strengthened our capabilities in terms of revealing common random factors from multiview datasets. In this work, we first revisit the most recent deterministic extensions of deep CCA and highlight the strengths and limitations of these state-of-the-art methods. Some methods allow trivial solutions, while others can miss weak common factors. Others overload the problem by also seeking to reveal what is not common among the views -- i.e., the private components that are needed to fully reconstruct each view. The latter tends to overload the problem and its computational and sample complexities. Aiming to improve upon these limitations, we design a novel and efficient formulation that alleviates some of the current restrictions. The main idea is to model the private components as conditionally independent given the common ones, which enables the proposed compact formulation. In addition, we also provide a sufficient condition for identifying the common random factors. Judicious experiments with synthetic and real datasets showcase the validity of our claims and the effectiveness of the proposed approach.

Multisubject Task-Related fMRI Data Processing via a Two-Stage Generalized Canonical Correlation Analysis

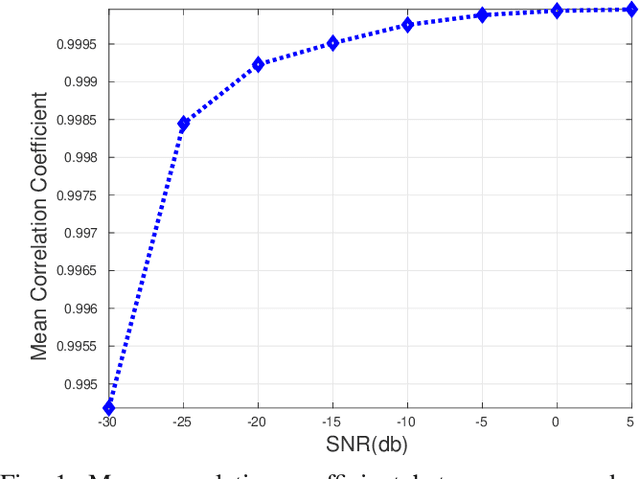
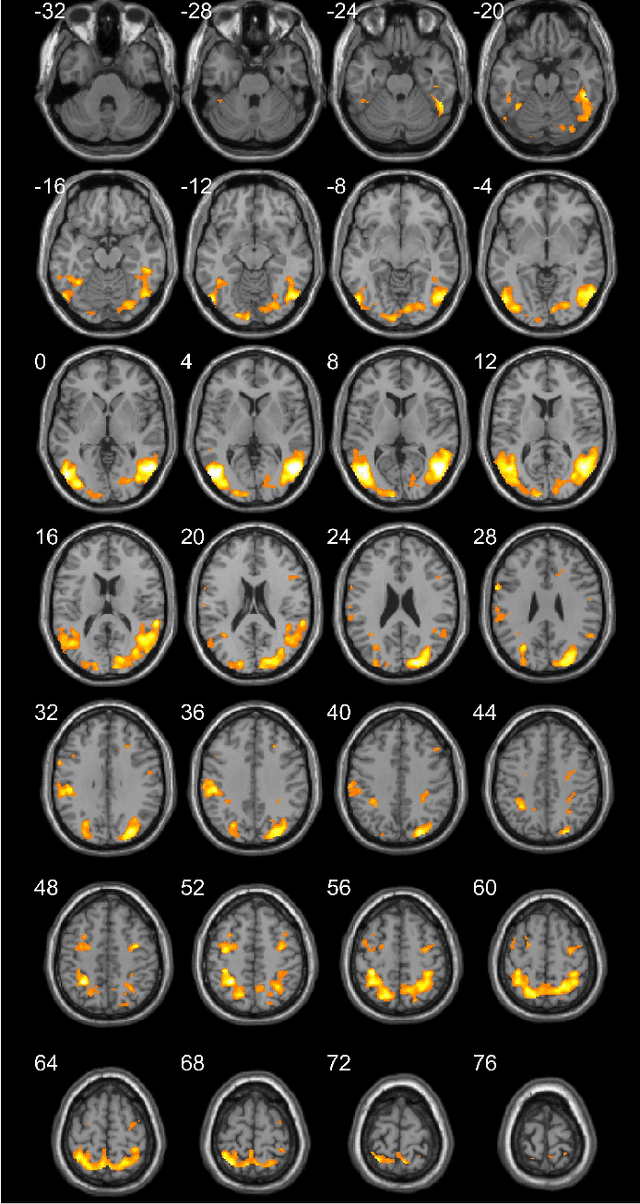
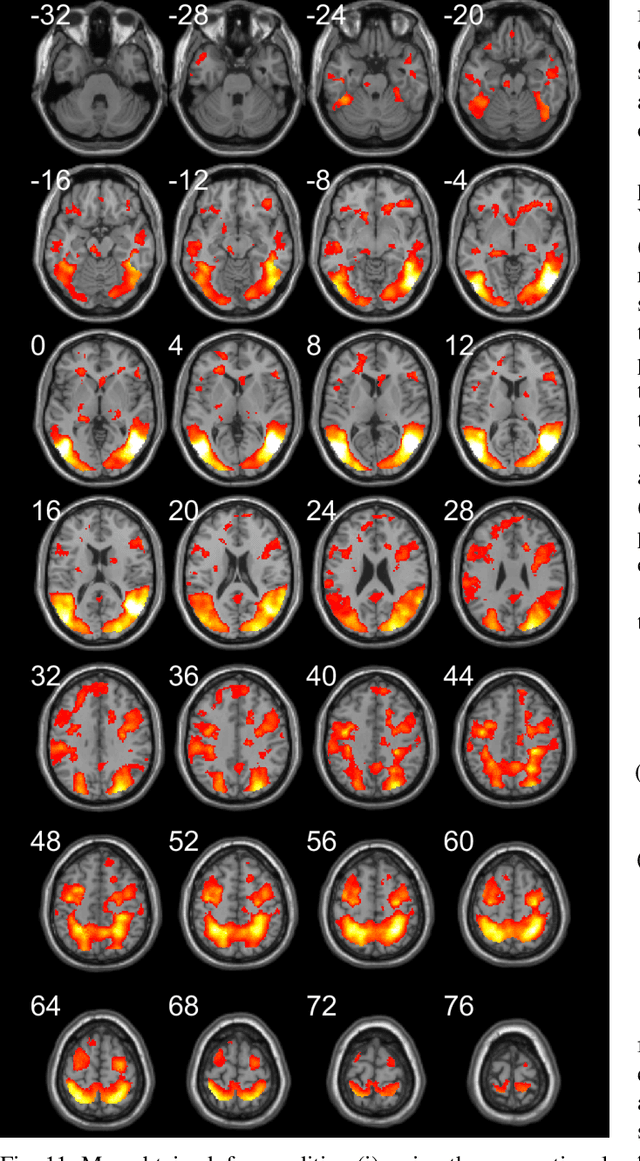
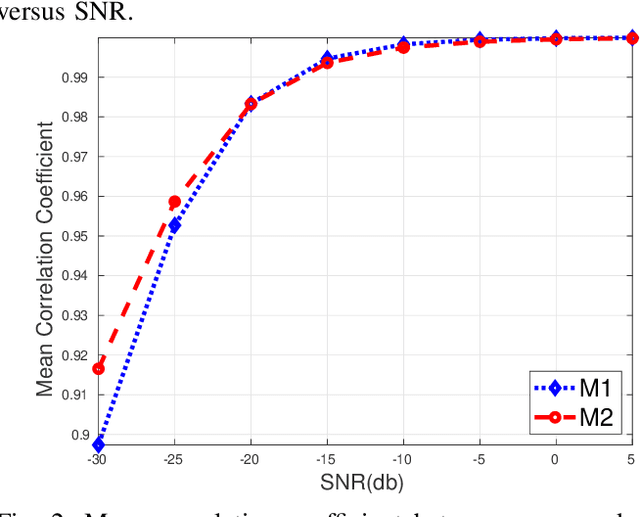
Functional magnetic resonance imaging (fMRI) is one of the most popular methods for studying the human brain. Task-related fMRI data processing aims to determine which brain areas are activated when a specific task is performed and is usually based on the Blood Oxygen Level Dependent (BOLD) signal. The background BOLD signal also reflects systematic fluctuations in regional brain activity which are attributed to the existence of resting-state brain networks. We propose a new fMRI data generating model which takes into consideration the existence of common task-related and resting-state components. We first estimate the common task-related temporal component, via two successive stages of generalized canonical correlation analysis and, then, we estimate the common task-related spatial component, leading to a task-related activation map. The experimental tests of our method with synthetic data reveal that we are able to obtain very accurate temporal and spatial estimates even at very low Signal to Noise Ratio (SNR), which is usually the case in fMRI data processing. The tests with real-world fMRI data show significant advantages over standard procedures based on General Linear Models (GLMs).