An Accelerated Stochastic Gradient for Canonical Polyadic Decomposition

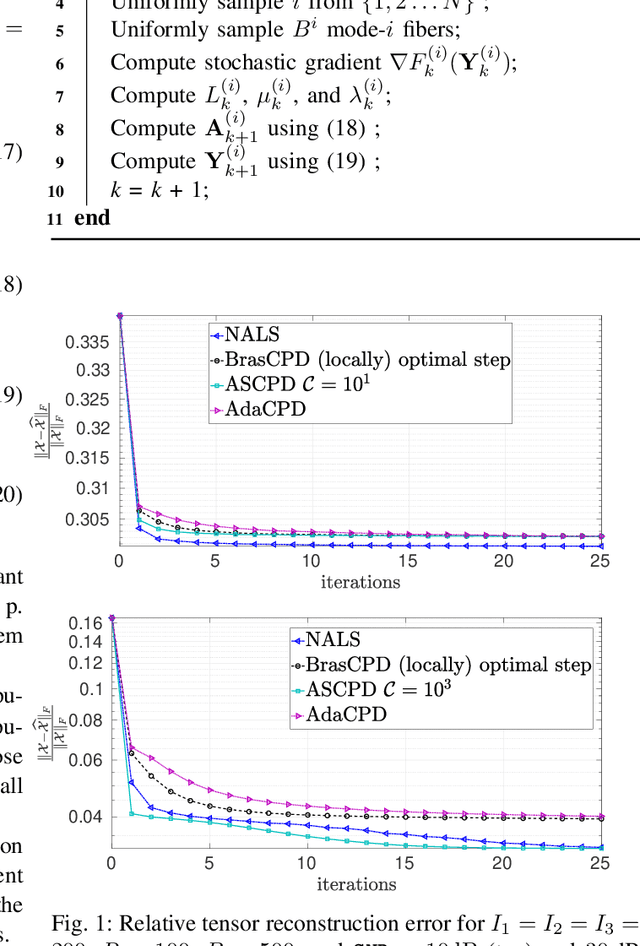
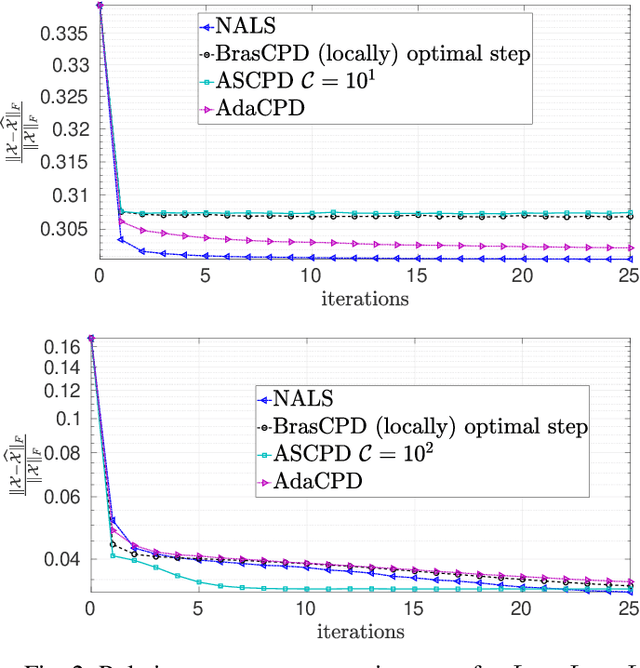
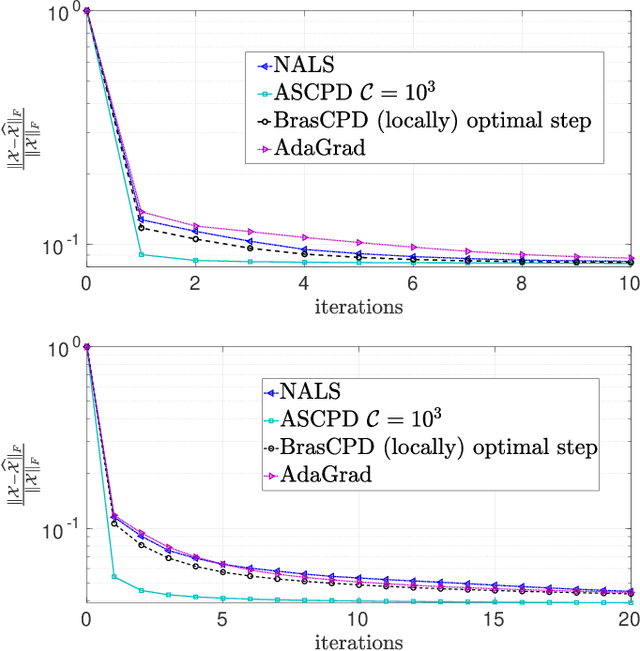
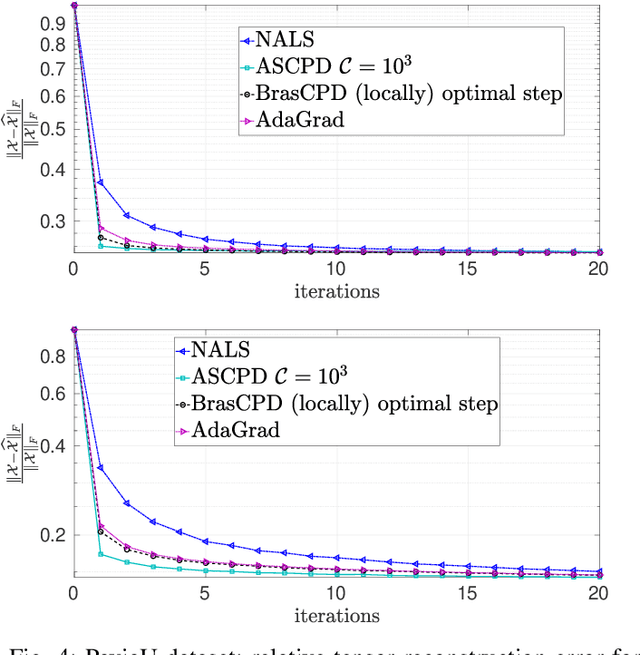
We consider the problem of structured canonical polyadic decomposition. If the size of the problem is very big, then stochastic gradient approaches are viable alternatives to classical methods, such as Alternating Optimization and All-At-Once optimization. We extend a recent stochastic gradient approach by employing an acceleration step (Nesterov momentum) in each iteration. We compare our approach with state-of-the-art alternatives, using both synthetic and real-world data, and find it to be very competitive.

Accelerated Stochastic Gradient for Nonnegative Tensor Completion and Parallel Implementation

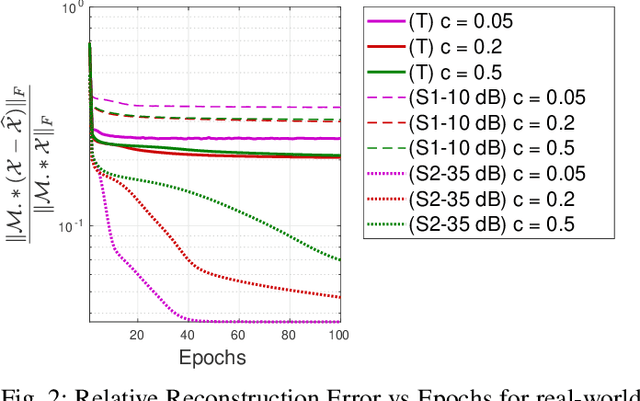
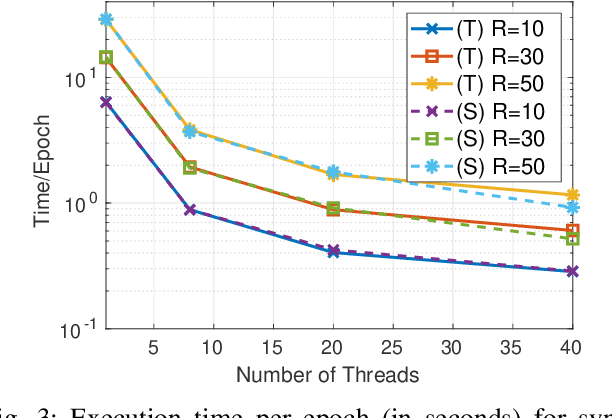
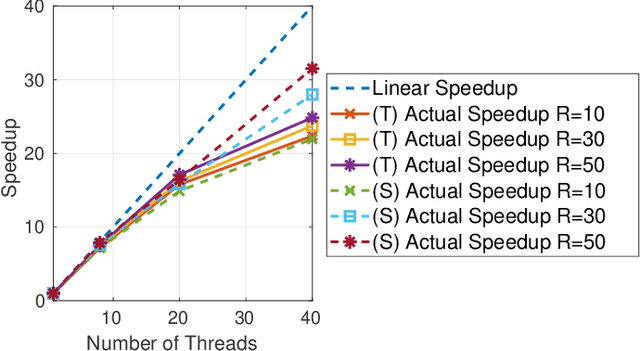
We consider the problem of nonnegative tensor completion. We adopt the alternating optimization framework and solve each nonnegative matrix completion problem via a stochastic variation of the accelerated gradient algorithm. We experimentally test the effectiveness and the efficiency of our algorithm using both real-world and synthetic data. We develop a shared-memory implementation of our algorithm using the multi-threaded API OpenMP, which attains significant speedup. We believe that our approach is a very competitive candidate for the solution of very large nonnegative tensor completion problems.