An Accelerated Stochastic Gradient for Canonical Polyadic Decomposition
Paper and Code
Sep 28, 2021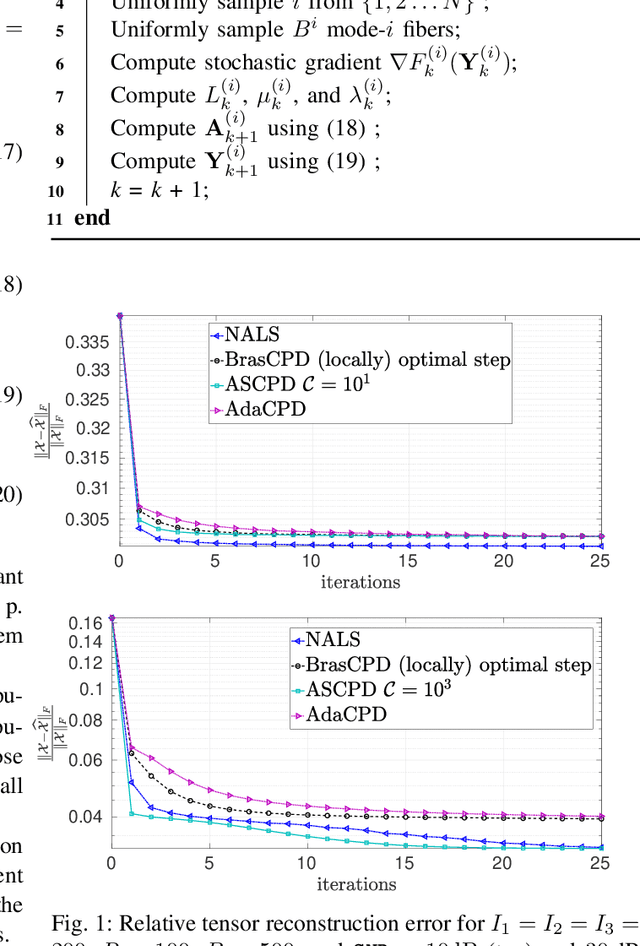
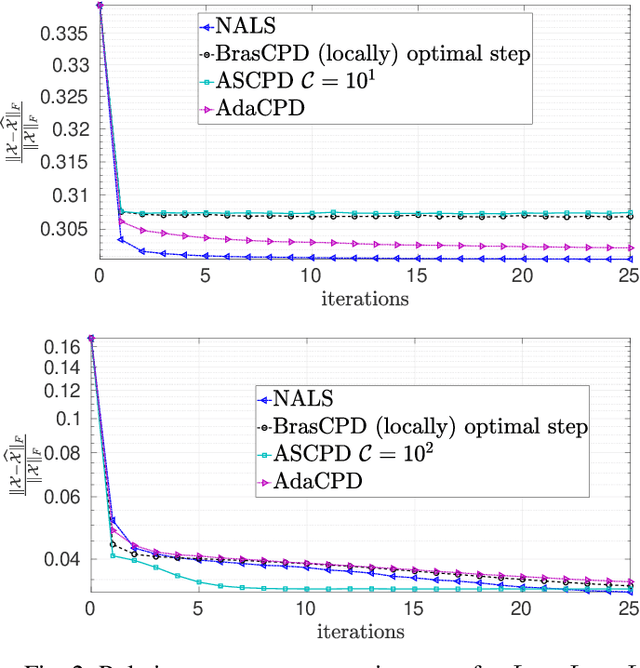
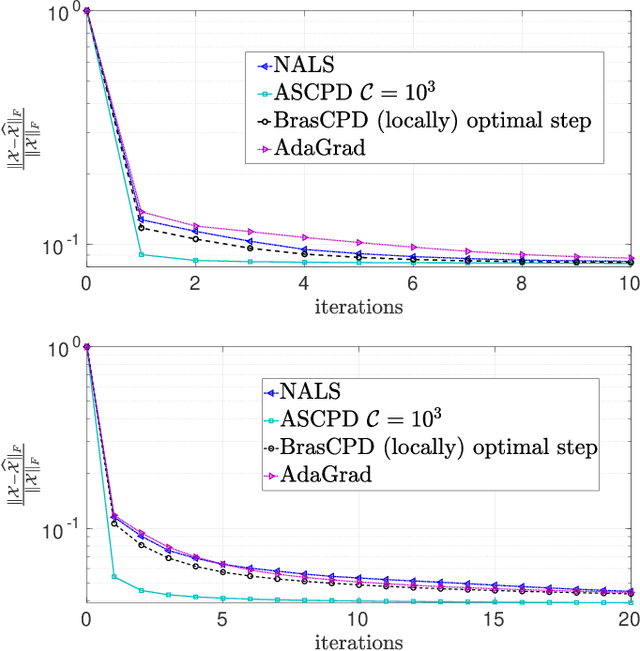
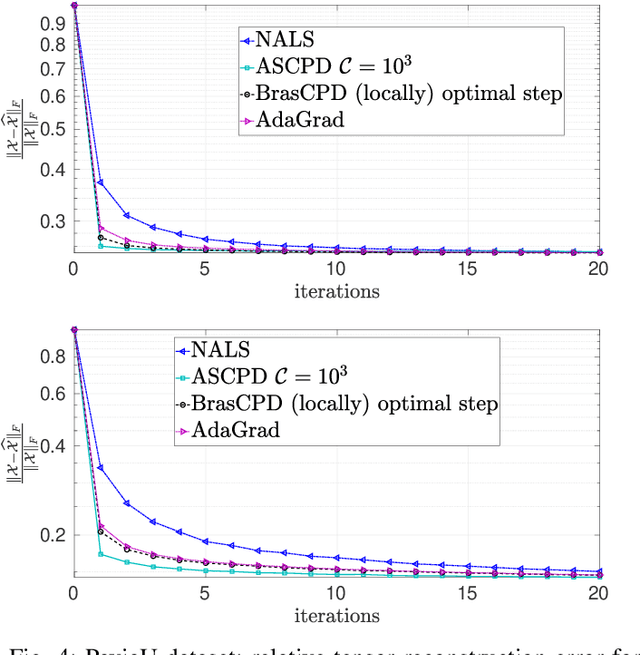
We consider the problem of structured canonical polyadic decomposition. If the size of the problem is very big, then stochastic gradient approaches are viable alternatives to classical methods, such as Alternating Optimization and All-At-Once optimization. We extend a recent stochastic gradient approach by employing an acceleration step (Nesterov momentum) in each iteration. We compare our approach with state-of-the-art alternatives, using both synthetic and real-world data, and find it to be very competitive.
* 5 pages, 4 figures, this work was accepted and presented at EUSIPCO
2021
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge