Generalizability of Graph Neural Networks for Decentralized Unlabeled Motion Planning

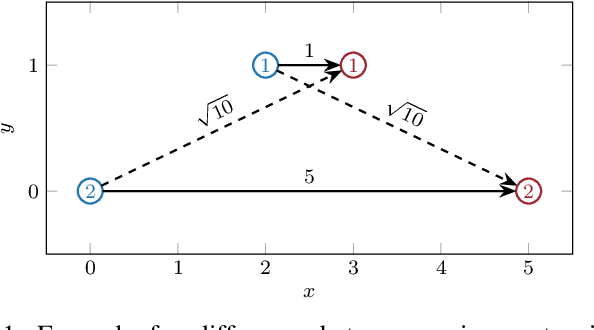
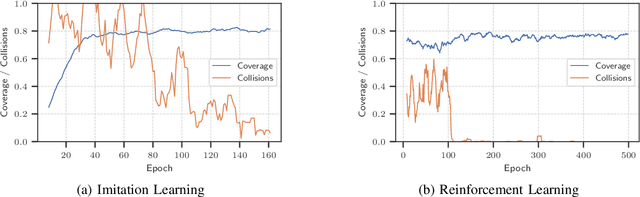
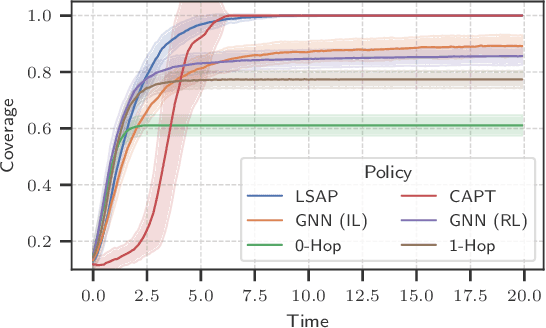
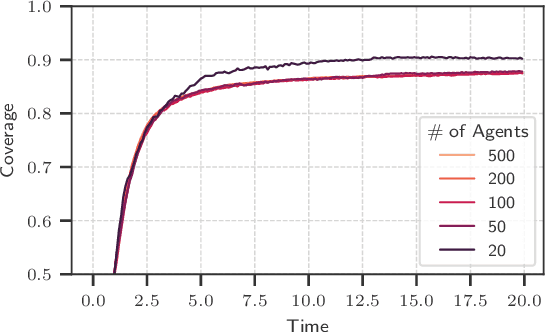
Unlabeled motion planning involves assigning a set of robots to target locations while ensuring collision avoidance, aiming to minimize the total distance traveled. The problem forms an essential building block for multi-robot systems in applications such as exploration, surveillance, and transportation. We address this problem in a decentralized setting where each robot knows only the positions of its $k$-nearest robots and $k$-nearest targets. This scenario combines elements of combinatorial assignment and continuous-space motion planning, posing significant scalability challenges for traditional centralized approaches. To overcome these challenges, we propose a decentralized policy learned via a Graph Neural Network (GNN). The GNN enables robots to determine (1) what information to communicate to neighbors and (2) how to integrate received information with local observations for decision-making. We train the GNN using imitation learning with the centralized Hungarian algorithm as the expert policy, and further fine-tune it using reinforcement learning to avoid collisions and enhance performance. Extensive empirical evaluations demonstrate the scalability and effectiveness of our approach. The GNN policy trained on 100 robots generalizes to scenarios with up to 500 robots, outperforming state-of-the-art solutions by 8.6\% on average and significantly surpassing greedy decentralized methods. This work lays the foundation for solving multi-robot coordination problems in settings where scalability is important.

Network Alignment with Transferable Graph Autoencoders

Network alignment is the task of establishing one-to-one correspondences between the nodes of different graphs and finds a plethora of applications in high-impact domains. However, this task is known to be NP-hard in its general form, and existing algorithms do not scale up as the size of the graphs increases. To tackle both challenges we propose a novel generalized graph autoencoder architecture, designed to extract powerful and robust node embeddings, that are tailored to the alignment task. We prove that the generated embeddings are associated with the eigenvalues and eigenvectors of the graphs and can achieve more accurate alignment compared to classical spectral methods. Our proposed framework also leverages transfer learning and data augmentation to achieve efficient network alignment at a very large scale without retraining. Extensive experiments on both network and sub-network alignment with real-world graphs provide corroborating evidence supporting the effectiveness and scalability of the proposed approach.

Transferability of Convolutional Neural Networks in Stationary Learning Tasks

Recent advances in hardware and big data acquisition have accelerated the development of deep learning techniques. For an extended period of time, increasing the model complexity has led to performance improvements for various tasks. However, this trend is becoming unsustainable and there is a need for alternative, computationally lighter methods. In this paper, we introduce a novel framework for efficient training of convolutional neural networks (CNNs) for large-scale spatial problems. To accomplish this we investigate the properties of CNNs for tasks where the underlying signals are stationary. We show that a CNN trained on small windows of such signals achieves a nearly performance on much larger windows without retraining. This claim is supported by our theoretical analysis, which provides a bound on the performance degradation. Additionally, we conduct thorough experimental analysis on two tasks: multi-target tracking and mobile infrastructure on demand. Our results show that the CNN is able to tackle problems with many hundreds of agents after being trained with fewer than ten. Thus, CNN architectures provide solutions to these problems at previously computationally intractable scales.

Solving Large-scale Spatial Problems with Convolutional Neural Networks

Over the past decade, deep learning research has been accelerated by increasingly powerful hardware, which facilitated rapid growth in the model complexity and the amount of data ingested. This is becoming unsustainable and therefore refocusing on efficiency is necessary. In this paper, we employ transfer learning to improve training efficiency for large-scale spatial problems. We propose that a convolutional neural network (CNN) can be trained on small windows of signals, but evaluated on arbitrarily large signals with little to no performance degradation, and provide a theoretical bound on the resulting generalization error. Our proof leverages shift-equivariance of CNNs, a property that is underexploited in transfer learning. The theoretical results are experimentally supported in the context of mobile infrastructure on demand (MID). The proposed approach is able to tackle MID at large scales with hundreds of agents, which was computationally intractable prior to this work.

Graph Neural Networks Are More Powerful Than we Think

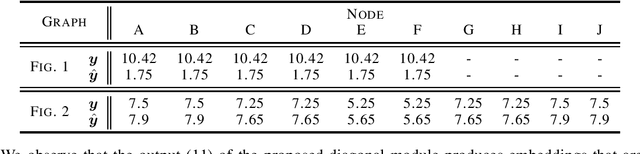
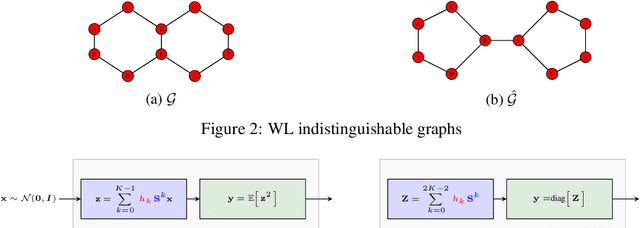
Graph Neural Networks (GNNs) are powerful convolutional architectures that have shown remarkable performance in various node-level and graph-level tasks. Despite their success, the common belief is that the expressive power of GNNs is limited and that they are at most as discriminative as the Weisfeiler-Lehman (WL) algorithm. In this paper we argue the opposite and show that the WL algorithm is the upper bound only when the input to the GNN is the vector of all ones. In this direction, we derive an alternative analysis that employs linear algebraic tools and characterize the representational power of GNNs with respect to the eigenvalue decomposition of the graph operators. We show that GNNs can distinguish between any graphs that differ in at least one eigenvalue and design simple GNN architectures that are provably more expressive than the WL algorithm. Thorough experimental analysis on graph isomorphism and graph classification datasets corroborates our theoretical results and demonstrates the effectiveness of the proposed architectures.

Space-Time Graph Neural Networks

We introduce space-time graph neural network (ST-GNN), a novel GNN architecture, tailored to jointly process the underlying space-time topology of time-varying network data. The cornerstone of our proposed architecture is the composition of time and graph convolutional filters followed by pointwise nonlinear activation functions. We introduce a generic definition of convolution operators that mimic the diffusion process of signals over its underlying support. On top of this definition, we propose space-time graph convolutions that are built upon a composition of time and graph shift operators. We prove that ST-GNNs with multivariate integral Lipschitz filters are stable to small perturbations in the underlying graphs as well as small perturbations in the time domain caused by time warping. Our analysis shows that small variations in the network topology and time evolution of a system does not significantly affect the performance of ST-GNNs. Numerical experiments with decentralized control systems showcase the effectiveness and stability of the proposed ST-GNNs.

GAGE: Geometry Preserving Attributed Graph Embeddings

Node representation learning is the task of extracting concise and informative feature embeddings of certain entities that are connected in a network. Many real world network datasets include information about both node connectivity and certain node attributes, in the form of features or time-series data. Modern representation learning techniques utilize both connectivity and attribute information of the nodes to produce embeddings in an unsupervised manner. In this context, deriving embeddings that preserve the geometry of the network and the attribute vectors would be highly desirable, as they would reflect both the topological neighborhood structure and proximity in feature space. While this is fairly straightforward to maintain when only observing the connectivity or attributed information of the network, preserving the geometry of both types of information is challenging. A novel tensor factorization approach for node embedding in attributed networks that preserves the distances of both the connections and the attributes is proposed in this paper, along with an effective and lightweight algorithm to tackle the learning task. Judicious experiments with multiple state-of-art baselines suggest that the proposed algorithm offers significant performance improvements in node classification and link prediction tasks.

TeX-Graph: Coupled tensor-matrix knowledge-graph embedding for COVID-19 drug repurposing

Knowledge graphs (KGs) are powerful tools that codify relational behaviour between entities in knowledge bases. KGs can simultaneously model many different types of subject-predicate-object and higher-order relations. As such, they offer a flexible modeling framework that has been applied to many areas, including biology and pharmacology -- most recently, in the fight against COVID-19. The flexibility of KG modeling is both a blessing and a challenge from the learning point of view. In this paper we propose a novel coupled tensor-matrix framework for KG embedding. We leverage tensor factorization tools to learn concise representations of entities and relations in knowledge bases and employ these representations to perform drug repurposing for COVID-19. Our proposed framework is principled, elegant, and achieves 100% improvement over the best baseline in the COVID-19 drug repurposing task using a recently developed biological KG.

Generalized Canonical Correlation Analysis: A Subspace Intersection Approach

Generalized Canonical Correlation Analysis (GCCA) is an important tool that finds numerous applications in data mining, machine learning, and artificial intelligence. It aims at finding `common' random variables that are strongly correlated across multiple feature representations (views) of the same set of entities. CCA and to a lesser extent GCCA have been studied from the statistical and algorithmic points of view, but not as much from the standpoint of linear algebra. This paper offers a fresh algebraic perspective of GCCA based on a (bi-)linear generative model that naturally captures its essence. It is shown that from a linear algebra point of view, GCCA is tantamount to subspace intersection; and conditions under which the common subspace of the different views is identifiable are provided. A novel GCCA algorithm is proposed based on subspace intersection, which scales up to handle large GCCA tasks. Synthetic as well as real data experiments are provided to showcase the effectiveness of the proposed approach.

PREMA: Principled Tensor Data Recovery from Multiple Aggregated Views

Multidimensional data have become ubiquitous and are frequently involved in situations where the information is aggregated over multiple data atoms. The aggregation can be over time or other features, such as geographical location or group affiliation. We often have access to multiple aggregated views of the same data, each aggregated in one or more dimensions, especially when data are collected or measured by different agencies. However, data mining and machine learning models require detailed data for personalized analysis and prediction. Thus, data disaggregation algorithms are becoming increasingly important in various domains. The goal of this paper is to reconstruct finer-scale data from multiple coarse views, aggregated over different (subsets of) dimensions. The proposed method, called PREMA, leverages low-rank tensor factorization tools to provide recovery guarantees under certain conditions. PREMA is flexible in the sense that it can perform disaggregation on data that have missing entries, i.e., partially observed. The proposed method considers challenging scenarios: i) the available views of the data are aggregated in two dimensions, i.e., double aggregation, and ii) the aggregation patterns are unknown. Experiments on real data from different domains, i.e., sales data from retail companies, crime counts, and weather observations, are presented to showcase the effectiveness of PREMA.