Vector-valued Distance and Gyrocalculus on the Space of Symmetric Positive Definite Matrices

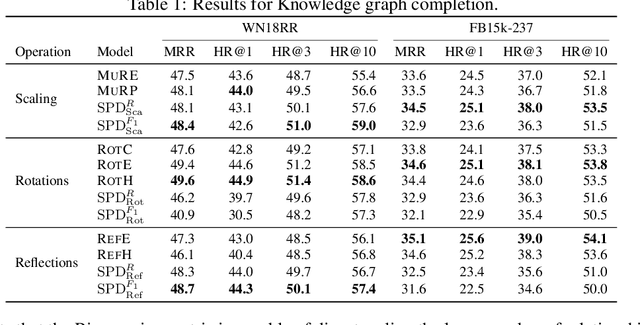
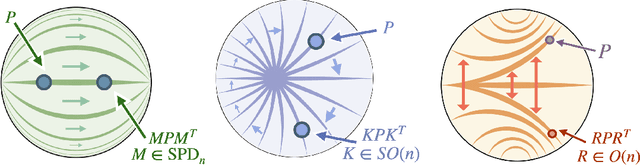
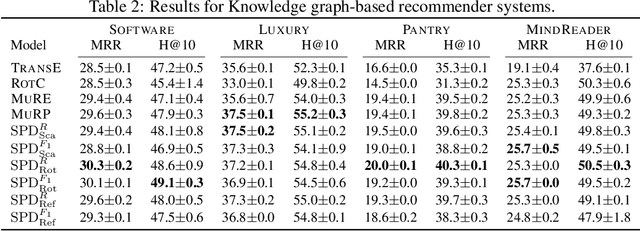
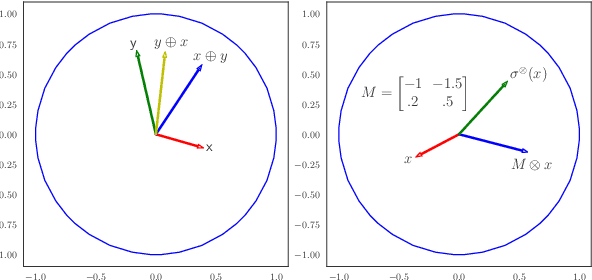
We propose the use of the vector-valued distance to compute distances and extract geometric information from the manifold of symmetric positive definite matrices (SPD), and develop gyrovector calculus, constructing analogs of vector space operations in this curved space. We implement these operations and showcase their versatility in the tasks of knowledge graph completion, item recommendation, and question answering. In experiments, the SPD models outperform their equivalents in Euclidean and hyperbolic space. The vector-valued distance allows us to visualize embeddings, showing that the models learn to disentangle representations of positive samples from negative ones.

Augmenting the User-Item Graph with Textual Similarity Models

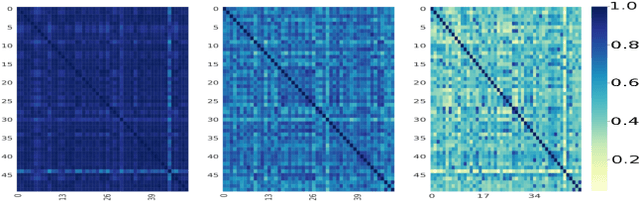
This paper introduces a simple and effective form of data augmentation for recommender systems. A paraphrase similarity model is applied to widely available textual data, such as reviews and product descriptions, yielding new semantic relations that are added to the user-item graph. This increases the density of the graph without needing further labeled data. The data augmentation is evaluated on a variety of recommendation algorithms, using Euclidean, hyperbolic, and complex spaces, and over three categories of Amazon product reviews with differing characteristics. Results show that the data augmentation technique provides significant improvements to all types of models, with the most pronounced gains for knowledge graph-based recommenders, particularly in cold-start settings, leading to state-of-the-art performance.

Symmetric Spaces for Graph Embeddings: A Finsler-Riemannian Approach

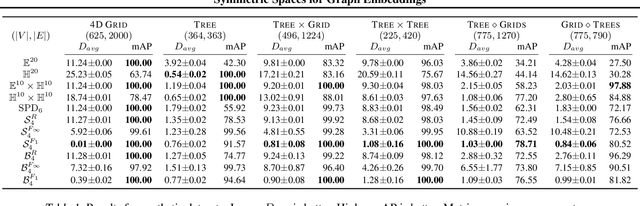
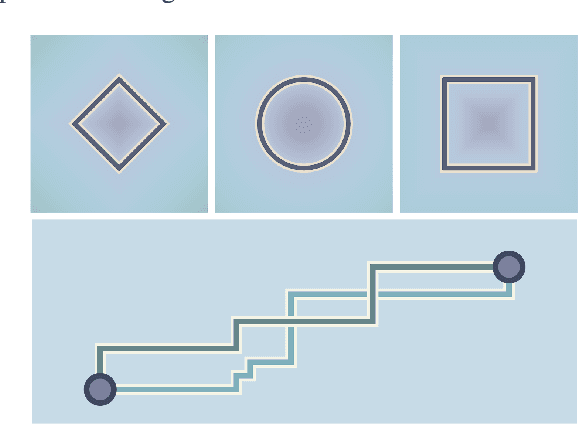
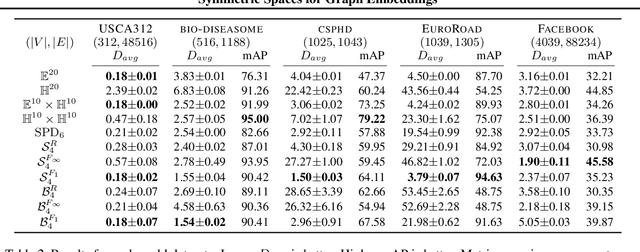
Learning faithful graph representations as sets of vertex embeddings has become a fundamental intermediary step in a wide range of machine learning applications. We propose the systematic use of symmetric spaces in representation learning, a class encompassing many of the previously used embedding targets. This enables us to introduce a new method, the use of Finsler metrics integrated in a Riemannian optimization scheme, that better adapts to dissimilar structures in the graph. We develop a tool to analyze the embeddings and infer structural properties of the data sets. For implementation, we choose Siegel spaces, a versatile family of symmetric spaces. Our approach outperforms competitive baselines for graph reconstruction tasks on various synthetic and real-world datasets. We further demonstrate its applicability on two downstream tasks, recommender systems and node classification.

Hermitian Symmetric Spaces for Graph Embeddings

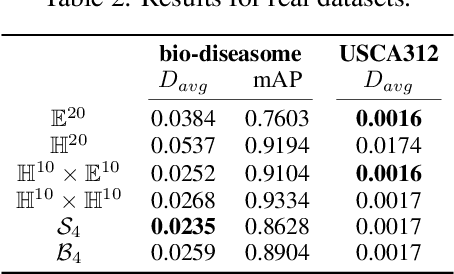
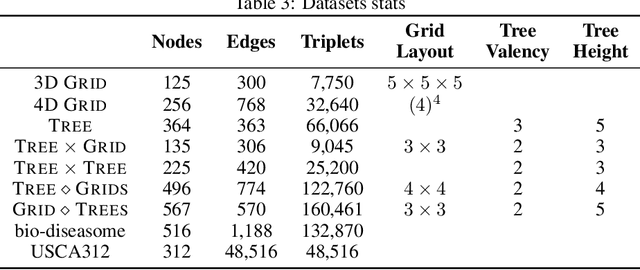
Learning faithful graph representations as sets of vertex embeddings has become a fundamental intermediary step in a wide range of machine learning applications. The quality of the embeddings is usually determined by how well the geometry of the target space matches the structure of the data. In this work we learn continuous representations of graphs in spaces of symmetric matrices over C. These spaces offer a rich geometry that simultaneously admits hyperbolic and Euclidean subspaces, and are amenable to analysis and explicit computations. We implement an efficient method to learn embeddings and compute distances, and develop the tools to operate with such spaces. The proposed models are able to automatically adapt to very dissimilar arrangements without any apriori estimates of graph features. On various datasets with very diverse structural properties and reconstruction measures our model ties the results of competitive baselines for geometrically pure graphs and outperforms them for graphs with mixed geometric features, showcasing the versatility of our approach.

A Fully Hyperbolic Neural Model for Hierarchical Multi-Class Classification

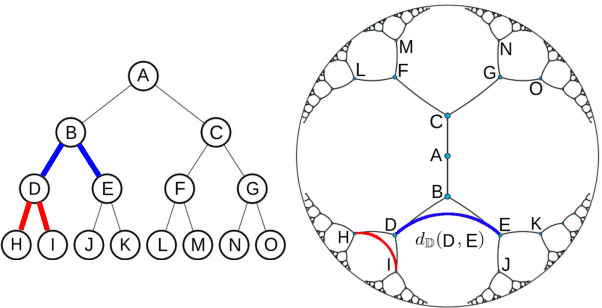
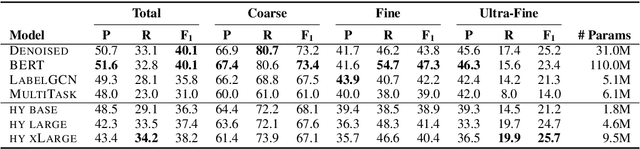
Label inventories for fine-grained entity typing have grown in size and complexity. Nonetheless, they exhibit a hierarchical structure. Hyperbolic spaces offer a mathematically appealing approach for learning hierarchical representations of symbolic data. However, it is not clear how to integrate hyperbolic components into downstream tasks. This is the first work that proposes a fully hyperbolic model for multi-class multi-label classification, which performs all operations in hyperbolic space. We evaluate the proposed model on two challenging datasets and compare to different baselines that operate under Euclidean assumptions. Our hyperbolic model infers the latent hierarchy from the class distribution, captures implicit hyponymic relations in the inventory, and shows performance on par with state-of-the-art methods on fine-grained classification with remarkable reduction of the parameter size. A thorough analysis sheds light on the impact of each component in the final prediction and showcases its ease of integration with Euclidean layers.

Fine-Grained Entity Typing in Hyperbolic Space

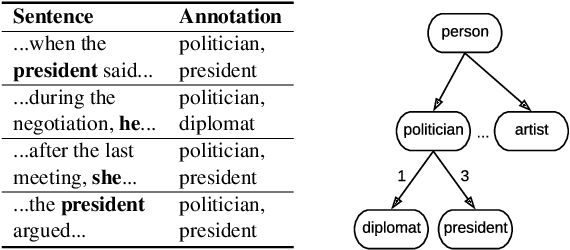
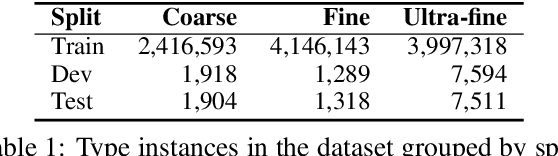
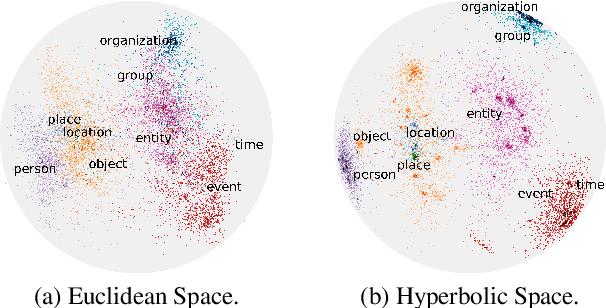
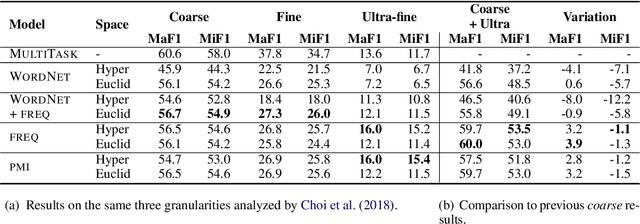
How can we represent hierarchical information present in large type inventories for entity typing? We study the ability of hyperbolic embeddings to capture hierarchical relations between mentions in context and their target types in a shared vector space. We evaluate on two datasets and investigate two different techniques for creating a large hierarchical entity type inventory: from an expert-generated ontology and by automatically mining type co-occurrences. We find that the hyperbolic model yields improvements over its Euclidean counterpart in some, but not all cases. Our analysis suggests that the adequacy of this geometry depends on the granularity of the type inventory and the way hierarchical relations are inferred.

Variations of the Similarity Function of TextRank for Automated Summarization

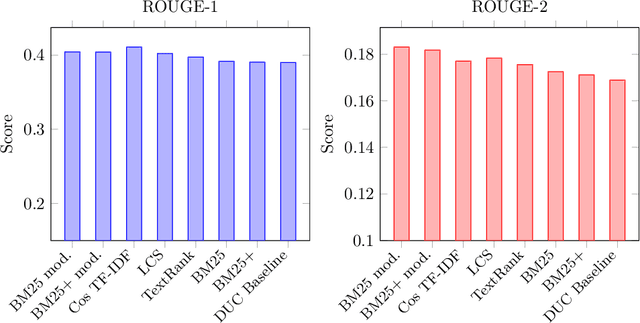
This article presents new alternatives to the similarity function for the TextRank algorithm for automatic summarization of texts. We describe the generalities of the algorithm and the different functions we propose. Some of these variants achieve a significative improvement using the same metrics and dataset as the original publication.