Faisal M. Almutairi
eTREE: Learning Tree-structured Embeddings
Dec 20, 2020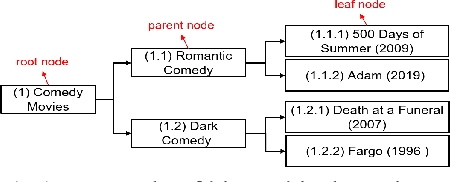
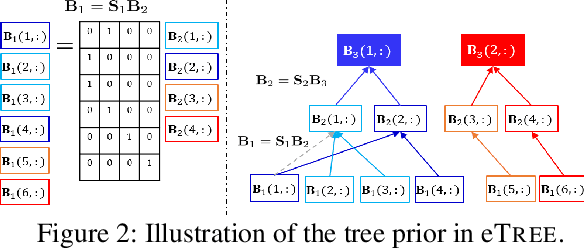

Abstract:Matrix factorization (MF) plays an important role in a wide range of machine learning and data mining models. MF is commonly used to obtain item embeddings and feature representations due to its ability to capture correlations and higher-order statistical dependencies across dimensions. In many applications, the categories of items exhibit a hierarchical tree structure. For instance, human diseases can be divided into coarse categories, e.g., bacterial, and viral. These categories can be further divided into finer categories, e.g., viral infections can be respiratory, gastrointestinal, and exanthematous viral diseases. In e-commerce, products, movies, books, etc., are grouped into hierarchical categories, e.g., clothing items are divided by gender, then by type (formal, casual, etc.). While the tree structure and the categories of the different items may be known in some applications, they have to be learned together with the embeddings in many others. In this work, we propose eTREE, a model that incorporates the (usually ignored) tree structure to enhance the quality of the embeddings. We leverage the special uniqueness properties of Nonnegative MF (NMF) to prove identifiability of eTREE. The proposed model not only exploits the tree structure prior, but also learns the hierarchical clustering in an unsupervised data-driven fashion. We derive an efficient algorithmic solution and a scalable implementation of eTREE that exploits parallel computing, computation caching, and warm start strategies. We showcase the effectiveness of eTREE on real data from various application domains: healthcare, recommender systems, and education. We also demonstrate the meaningfulness of the tree obtained from eTREE by means of domain experts interpretation.
PHASED: Phase-Aware Submodularity-Based Energy Disaggregation
Oct 01, 2020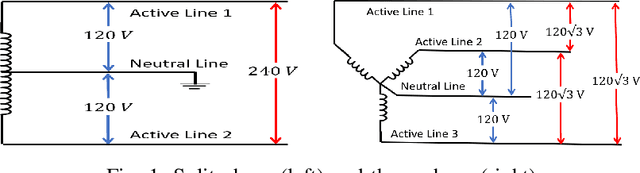
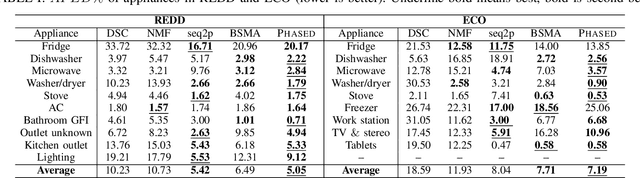
Abstract:Energy disaggregation is the task of discerning the energy consumption of individual appliances from aggregated measurements, which holds promise for understanding and reducing energy usage. In this paper, we propose PHASED, an optimization approach for energy disaggregation that has two key features: PHASED (i) exploits the structure of power distribution systems to make use of readily available measurements that are neglected by existing methods, and (ii) poses the problem as a minimization of a difference of submodular functions. We leverage this form by applying a discrete optimization variant of the majorization-minimization algorithm to iteratively minimize a sequence of global upper bounds of the cost function to obtain high-quality approximate solutions. PHASED improves the disaggregation accuracy of state-of-the-art models by up to 61% and achieves better prediction on heavy load appliances.
PREMA: Principled Tensor Data Recovery from Multiple Aggregated Views
Oct 26, 2019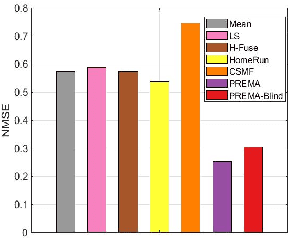

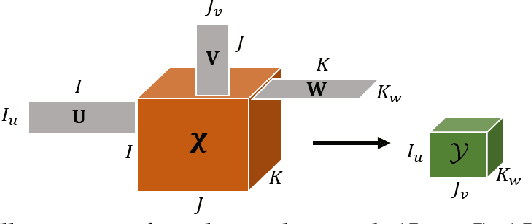
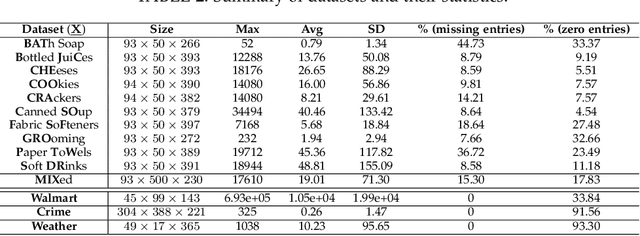
Abstract:Multidimensional data have become ubiquitous and are frequently involved in situations where the information is aggregated over multiple data atoms. The aggregation can be over time or other features, such as geographical location or group affiliation. We often have access to multiple aggregated views of the same data, each aggregated in one or more dimensions, especially when data are collected or measured by different agencies. However, data mining and machine learning models require detailed data for personalized analysis and prediction. Thus, data disaggregation algorithms are becoming increasingly important in various domains. The goal of this paper is to reconstruct finer-scale data from multiple coarse views, aggregated over different (subsets of) dimensions. The proposed method, called PREMA, leverages low-rank tensor factorization tools to provide recovery guarantees under certain conditions. PREMA is flexible in the sense that it can perform disaggregation on data that have missing entries, i.e., partially observed. The proposed method considers challenging scenarios: i) the available views of the data are aggregated in two dimensions, i.e., double aggregation, and ii) the aggregation patterns are unknown. Experiments on real data from different domains, i.e., sales data from retail companies, crime counts, and weather observations, are presented to showcase the effectiveness of PREMA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge