Ruiyuan Wu
SEAD: Self-Evolving Agent for Multi-Turn Service Dialogue
Feb 03, 2026Abstract:Large Language Models have demonstrated remarkable capabilities in open-domain dialogues. However, current methods exhibit suboptimal performance in service dialogues, as they rely on noisy, low-quality human conversation data. This limitation arises from data scarcity and the difficulty of simulating authentic, goal-oriented user behaviors. To address these issues, we propose SEAD (Self-Evolving Agent for Service Dialogue), a framework that enables agents to learn effective strategies without large-scale human annotations. SEAD decouples user modeling into two components: a Profile Controller that generates diverse user states to manage training curriculum, and a User Role-play Model that focuses on realistic role-playing. This design ensures the environment provides adaptive training scenarios rather than acting as an unfair adversary. Experiments demonstrate that SEAD significantly outperforms Open-source Foundation Models and Closed-source Commercial Models, improving task completion rate by 17.6% and dialogue efficiency by 11.1%. Code is available at: https://github.com/Da1yuqin/SEAD.
Memory-Efficient Convex Optimization for Self-Dictionary Separable Nonnegative Matrix Factorization: A Frank-Wolfe Approach
Sep 23, 2021



Abstract:Nonnegative matrix factorization (NMF) often relies on the separability condition for tractable algorithm design. Separability-based NMF is mainly handled by two types of approaches, namely, greedy pursuit and convex programming. A notable convex NMF formulation is the so-called self-dictionary multiple measurement vectors (SD-MMV), which can work without knowing the matrix rank a priori, and is arguably more resilient to error propagation relative to greedy pursuit. However, convex SD-MMV renders a large memory cost that scales quadratically with the problem size. This memory challenge has been around for a decade, and a major obstacle for applying convex SD-MMV to big data analytics. This work proposes a memory-efficient algorithm for convex SD-MMV. Our algorithm capitalizes on the special update rules of a classic algorithm from the 1950s, namely, the Frank-Wolfe (FW) algorithm. It is shown that, under reasonable conditions, the FW algorithm solves the noisy SD-MMV problem with a memory cost that grows linearly with the amount of data. To handle noisier scenarios, a smoothed group sparsity regularizer is proposed to improve robustness while maintaining the low memory footprint with guarantees. The proposed approach presents the first linear memory complexity algorithmic framework for convex SD-MMV based NMF. The method is tested over a couple of unsupervised learning tasks, i.e., text mining and community detection, to showcase its effectiveness and memory efficiency.
Probabilistic Simplex Component Analysis
Mar 18, 2021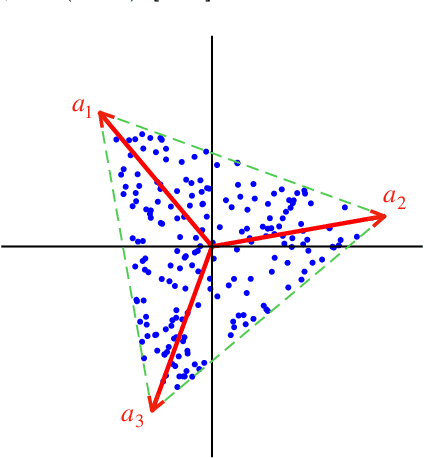
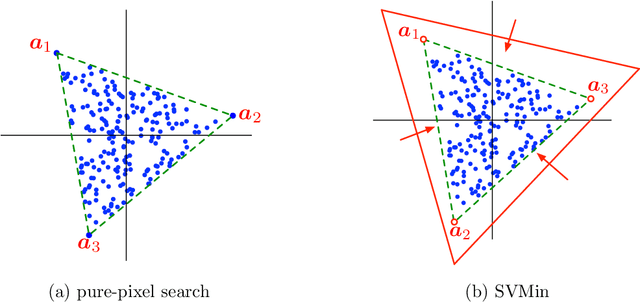

Abstract:This study presents PRISM, a probabilistic simplex component analysis approach to identifying the vertices of a data-circumscribing simplex from data. The problem has a rich variety of applications, the most notable being hyperspectral unmixing in remote sensing and non-negative matrix factorization in machine learning. PRISM uses a simple probabilistic model, namely, uniform simplex data distribution and additive Gaussian noise, and it carries out inference by maximum likelihood. The inference model is sound in the sense that the vertices are provably identifiable under some assumptions, and it suggests that PRISM can be effective in combating noise when the number of data points is large. PRISM has strong, but hidden, relationships with simplex volume minimization, a powerful geometric approach for the same problem. We study these fundamental aspects, and we also consider algorithmic schemes based on importance sampling and variational inference. In particular, the variational inference scheme is shown to resemble a matrix factorization problem with a special regularizer, which draws an interesting connection to the matrix factorization approach. Numerical results are provided to demonstrate the potential of PRISM.
Hyperspectral Super-Resolution via Global-Local Low-Rank Matrix Estimation
Jul 02, 2019



Abstract:Hyperspectral super-resolution (HSR) is a problem that aims to estimate an image of high spectral and spatial resolutions from a pair of co-registered multispectral (MS) and hyperspectral (HS) images, which have coarser spectral and spatial resolutions, respectively. In this paper we pursue a low-rank matrix estimation approach for HSR. We assume that the spectral-spatial matrices associated with the whole image and the local areas of the image have low rank structures. The local low-rank assumption, in particular, has the aim of providing a more flexible model for accounting for local variation effects due to endmember variability. We formulate the HSR problem as a global-local rank-regularized least-squares problem. By leveraging on the recent advances in non-convex large-scale optimization, namely, the smooth Schatten-p approximation and the accelerated majorization-minimization method, we developed an efficient algorithm for the global-local low-rank problem. Numerical experiments on synthetic and semi-real data show that the proposed algorithm outperforms a number of benchmark algorithms in terms of recovery performance.
Maximum Volume Inscribed Ellipsoid: A New Simplex-Structured Matrix Factorization Framework via Facet Enumeration and Convex Optimization
Jun 21, 2018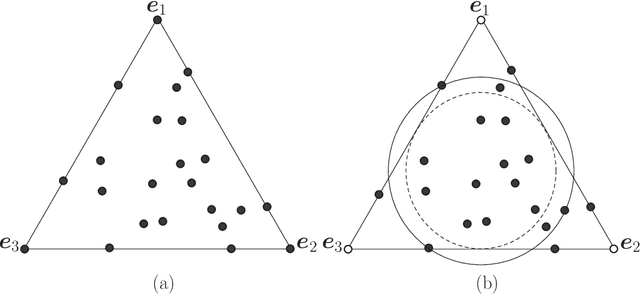
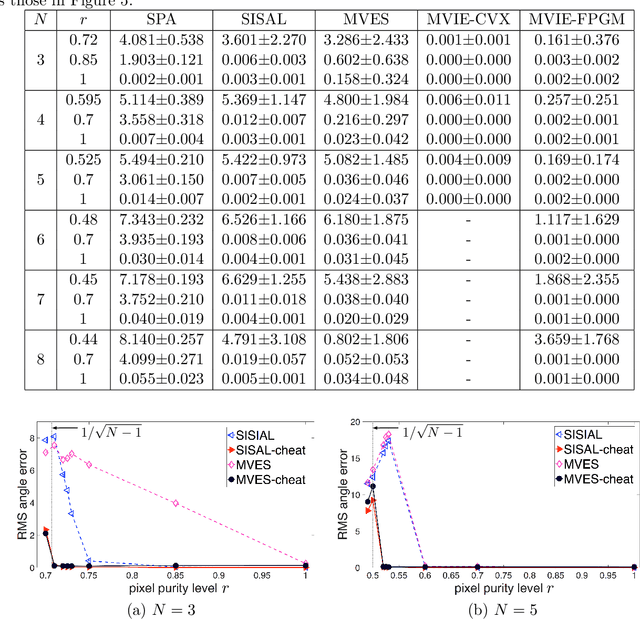
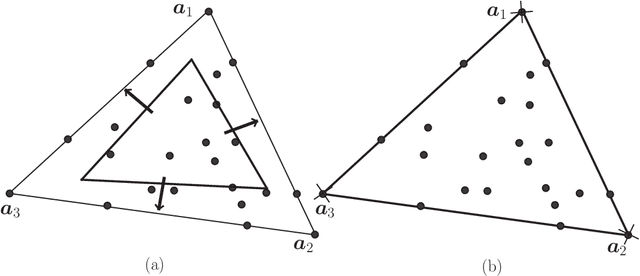
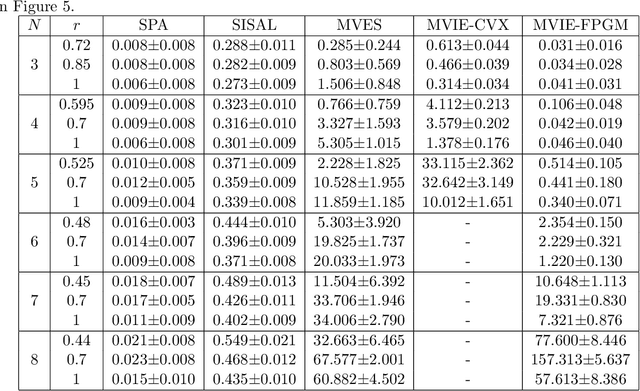
Abstract:Consider a structured matrix factorization model where one factor is restricted to have its columns lying in the unit simplex. This simplex-structured matrix factorization (SSMF) model and the associated factorization techniques have spurred much interest in research topics over different areas, such as hyperspectral unmixing in remote sensing, topic discovery in machine learning, to name a few. In this paper we develop a new theoretical SSMF framework whose idea is to study a maximum volume ellipsoid inscribed in the convex hull of the data points. This maximum volume inscribed ellipsoid (MVIE) idea has not been attempted in prior literature, and we show a sufficient condition under which the MVIE framework guarantees exact recovery of the factors. The sufficient recovery condition we show for MVIE is much more relaxed than that of separable non-negative matrix factorization (or pure-pixel search); coincidentally it is also identical to that of minimum volume enclosing simplex, which is known to be a powerful SSMF framework for non-separable problem instances. We also show that MVIE can be practically implemented by performing facet enumeration and then by solving a convex optimization problem. The potential of the MVIE framework is illustrated by numerical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge