A parametric non-negative coupled canonical polyadic decomposition algorithm for hyperspectral super-resolution

Recently, coupled tensor decomposition has been widely used in data fusion of a hyperspectral image (HSI) and a multispectral image (MSI) for hyperspectral super-resolution (HSR). However, exsiting works often ignore the inherent non-negative (NN) property of the image data, or impose the NN constraint via hard-thresholding which may interfere with the optimization procedure and cause the method to be sub-optimal. As such, we propose a novel NN coupled canonical polyadic decomposition (NN-C-CPD) algorithm, which makes use of the parametric method and nonlinear least squares (NLS) framework to impose the NN constraint into the C-CPD computation. More exactly, the NN constraint is converted into the squared relationship between the NN entries of the factor matrices and a set of latent parameters. Based on the chain rule for deriving the derivatives, the key entities such as gradient and Jacobian with regards to the latent parameters can be derived, thus the NN constraint is naturally integrated without interfering with the optimization procedure. Experimental results are provided to demonstrate the performance of the proposed NN-C-CPD algorithm in HSR applications.

A Block Term Decomposition Model Based Algorithm for Tensor Completion of Multidimensional Harmonic Signals

We consider tensor data completion of an incomplete observation of multidimensional harmonic (MH) signals. Unlike existing tensor-based techniques for MH retrieval (MHR), which mostly adopt the canonical polyadic decomposition (CPD) to model the simple "one-to-one" correspondence among harmonics across difference modes, we herein use the more flexible block term decomposition (BTD) model that can be used to describe the complex mutual correspondences among several groups of harmonics across different modes. An optimization principle that aims to fit the BTD model in the least squares sense, subject to rank minimization of hankelized MH components, is set up for the tensor completion task, and an algorithm based on alternating direction method of multipliers is proposed, of which the effectiveness and applicability are validated through both numerical simulations and an application in Sub-6GHz channel state information (CSI) completion.

A Coupled Random Projection Approach to Large-Scale Canonical Polyadic Decomposition

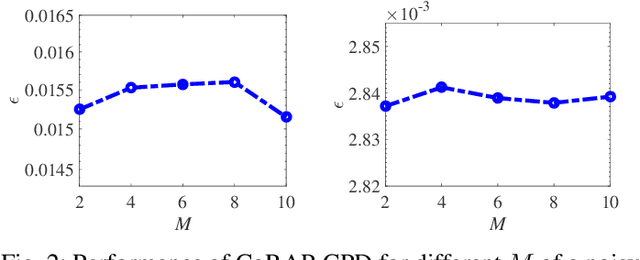
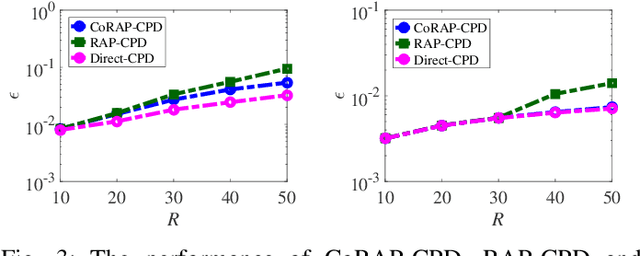
We propose a novel algorithm for the computation of canonical polyadic decomposition (CPD) of large-scale tensors. The proposed algorithm generalizes the random projection (RAP) technique, which is often used to compute large-scale decompositions, from one single projection to multiple but coupled random projections (CoRAP). The proposed CoRAP technique yields a set of tensors that together admits a coupled CPD (C-CPD) and a C-CPD algorithm is then used to jointly decompose these tensors. The results of C-CPD are finally fused to obtain factor matrices of the original large-scale data tensor. As more data samples are jointly exploited via C-CPD, the proposed CoRAP based CPD is more accurate than RAP based CPD. Experiments are provided to illustrate the performance of the proposed approach.

Double Coupled Canonical Polyadic Decomposition for Joint Blind Source Separation

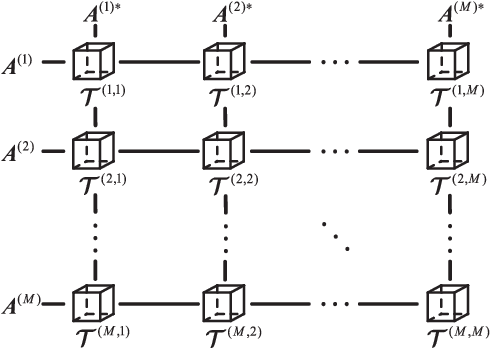
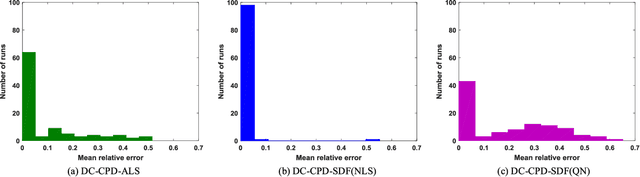
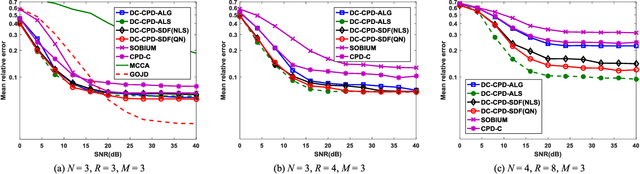
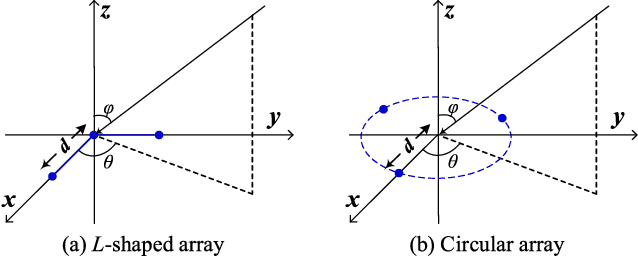
Joint blind source separation (J-BSS) is an emerging data-driven technique for multi-set data-fusion. In this paper, J-BSS is addressed from a tensorial perspective. We show how, by using second-order multi-set statistics in J-BSS, a specific double coupled canonical polyadic decomposition (DC-CPD) problem can be formulated. We propose an algebraic DC-CPD algorithm based on a coupled rank-1 detection mapping. This algorithm converts a possibly underdetermined DC-CPD to a set of overdetermined CPDs. The latter can be solved algebraically via a generalized eigenvalue decomposition based scheme. Therefore, this algorithm is deterministic and returns the exact solution in the noiseless case. In the noisy case, it can be used to effectively initialize optimization based DC-CPD algorithms. In addition, we obtain the determini- stic and generic uniqueness conditions for DC-CPD, which are shown to be more relaxed than their CPD counterpart. Experiment results are given to illustrate the superiority of DC-CPD over standard CPD based BSS methods and several existing J-BSS methods, with regards to uniqueness and accuracy.

Combined Independent Component Analysis and Canonical Polyadic Decomposition via Joint Diagonalization

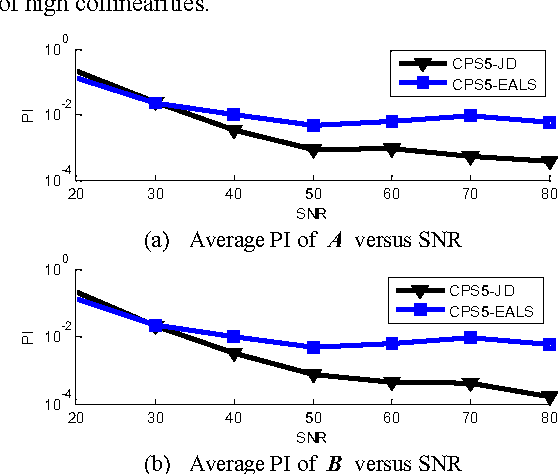
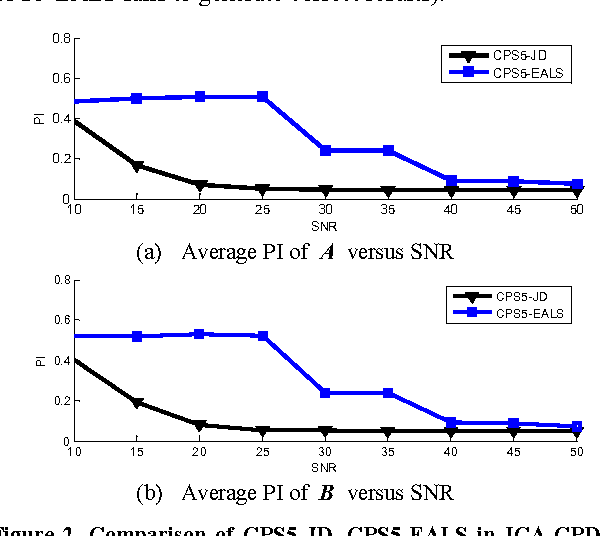
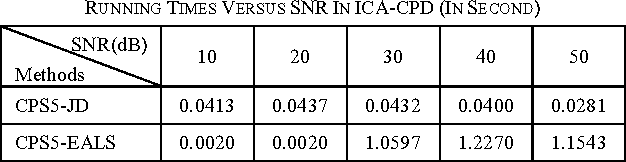
Recently, there has been a trend to combine independent component analysis and canonical polyadic decomposition (ICA-CPD) for an enhanced robustness for the computation of CPD, and ICA-CPD could be further converted into CPD of a 5th-order partially symmetric tensor, by calculating the eigenmatrices of the 4th-order cumulant slices of a trilinear mixture. In this study, we propose a new 5th-order CPD algorithm constrained with partial symmetry based on joint diagonalization. As the main steps involved in the proposed algorithm undergo no updating iterations for the loading matrices, it is much faster than the existing algorithm based on alternating least squares and enhanced line search, with competent performances. Simulation results are provided to demonstrate the performance of the proposed algorithm.

Generalized Non-orthogonal Joint Diagonalization with LU Decomposition and Successive Rotations

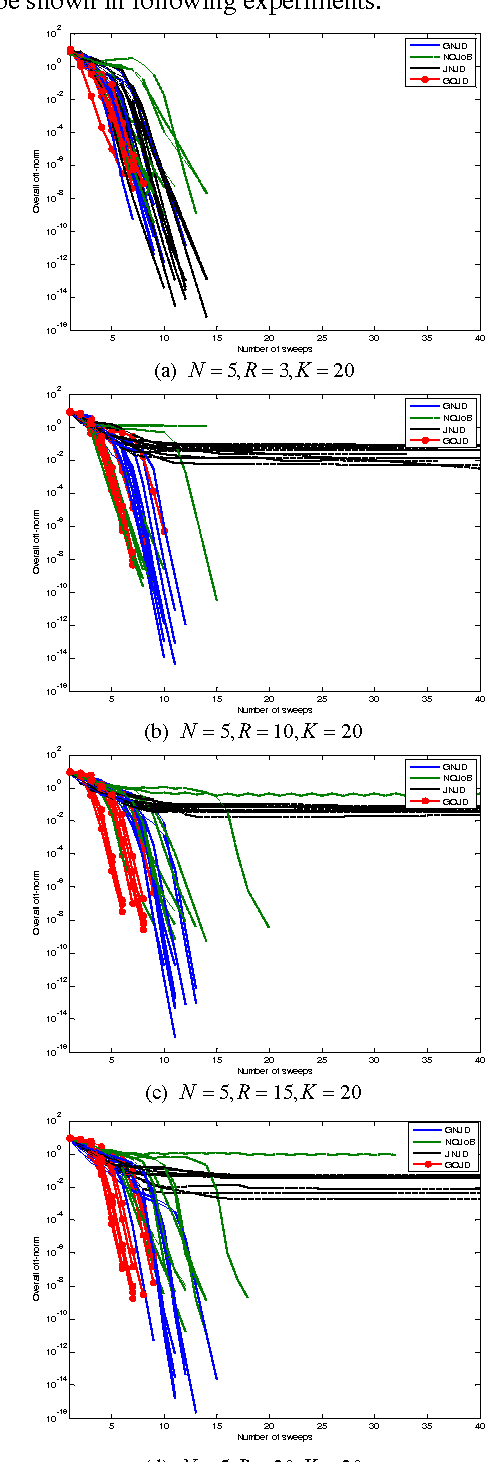
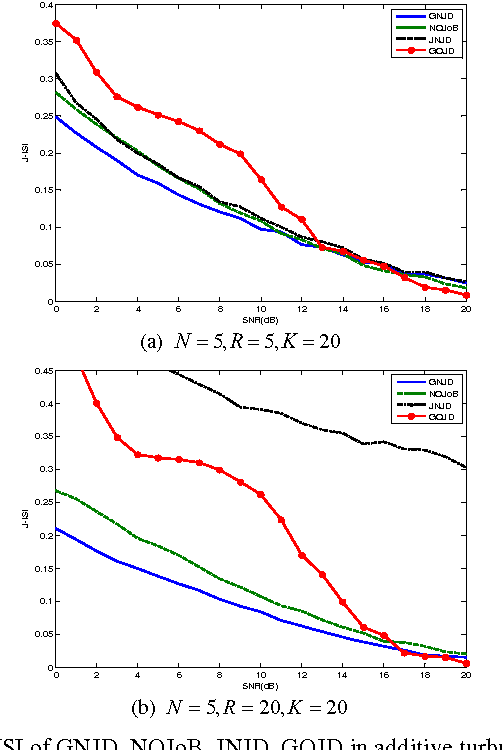
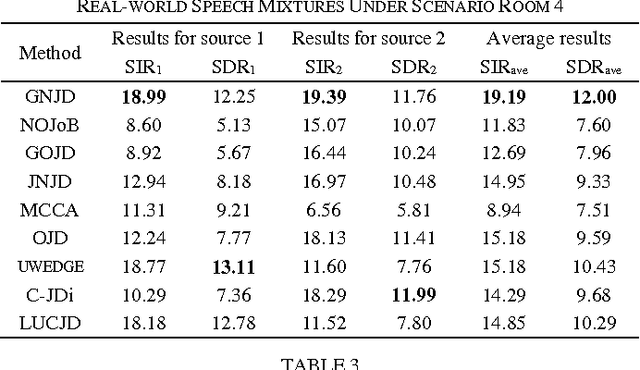
Non-orthogonal joint diagonalization (NJD) free of prewhitening has been widely studied in the context of blind source separation (BSS) and array signal processing, etc. However, NJD is used to retrieve the jointly diagonalizable structure for a single set of target matrices which are mostly formulized with a single dataset, and thus is insufficient to handle multiple datasets with inter-set dependences, a scenario often encountered in joint BSS (J-BSS) applications. As such, we present a generalized NJD (GNJD) algorithm to simultaneously perform asymmetric NJD upon multiple sets of target matrices with mutually linked loading matrices, by using LU decomposition and successive rotations, to enable J-BSS over multiple datasets with indication/exploitation of their mutual dependences. Experiments with synthetic and real-world datasets are provided to illustrate the performance of the proposed algorithm.