Ya-Na Hao
Combined Independent Component Analysis and Canonical Polyadic Decomposition via Joint Diagonalization
Dec 28, 2016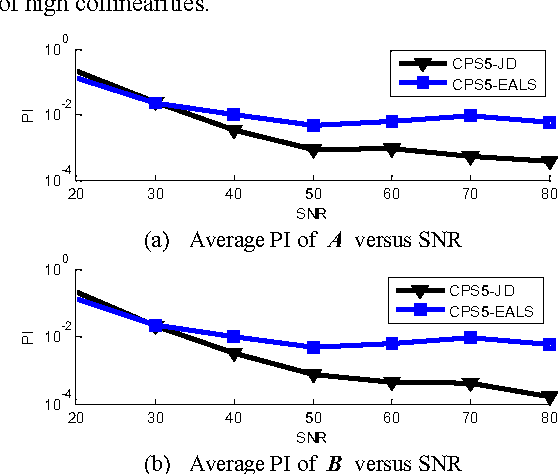
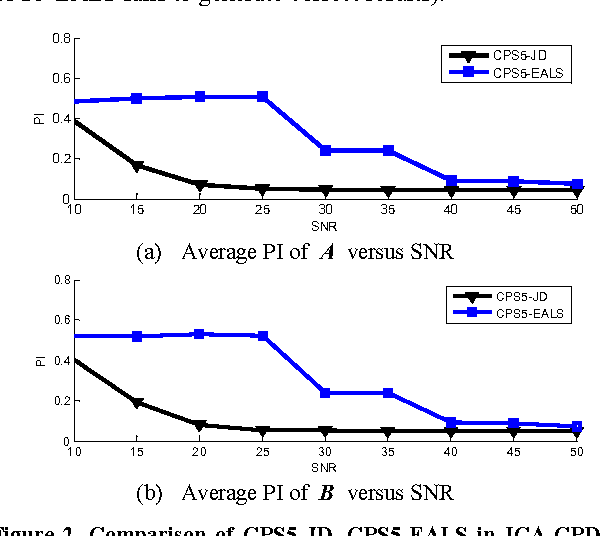
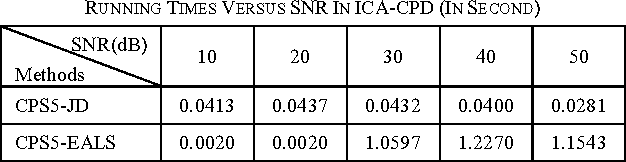
Abstract:Recently, there has been a trend to combine independent component analysis and canonical polyadic decomposition (ICA-CPD) for an enhanced robustness for the computation of CPD, and ICA-CPD could be further converted into CPD of a 5th-order partially symmetric tensor, by calculating the eigenmatrices of the 4th-order cumulant slices of a trilinear mixture. In this study, we propose a new 5th-order CPD algorithm constrained with partial symmetry based on joint diagonalization. As the main steps involved in the proposed algorithm undergo no updating iterations for the loading matrices, it is much faster than the existing algorithm based on alternating least squares and enhanced line search, with competent performances. Simulation results are provided to demonstrate the performance of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge