The Dice loss in the context of missing or empty labels: Introducing $Φ$ and $ε$

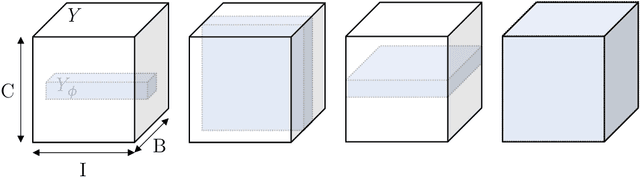
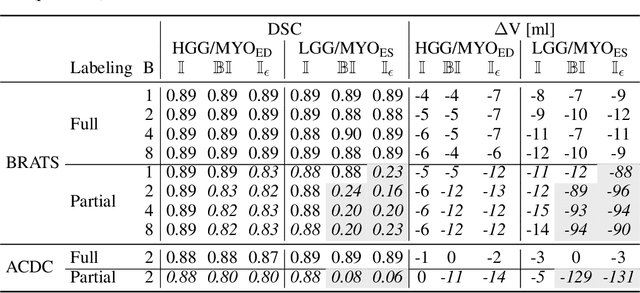
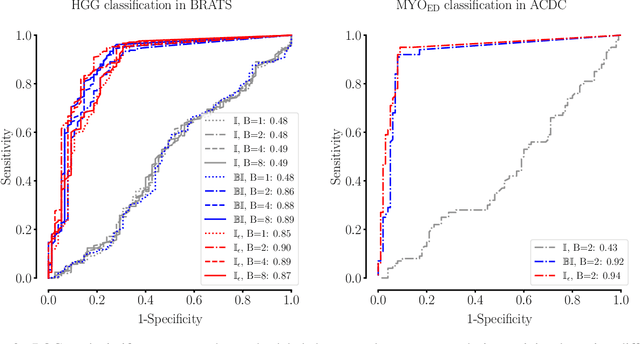
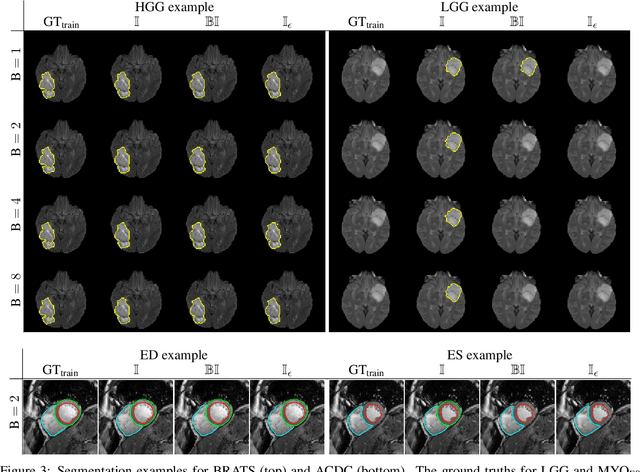
Albeit the Dice loss is one of the dominant loss functions in medical image segmentation, most research omits a closer look at its derivative, i.e. the real motor of the optimization when using gradient descent. In this paper, we highlight the peculiar action of the Dice loss in the presence of missing or empty labels. First, we formulate a theoretical basis that gives a general description of the Dice loss and its derivative. It turns out that the choice of the reduction dimensions $\Phi$ and the smoothing term $\epsilon$ is non-trivial and greatly influences its behavior. We find and propose heuristic combinations of $\Phi$ and $\epsilon$ that work in a segmentation setting with either missing or empty labels. Second, we empirically validate these findings in a binary and multiclass segmentation setting using two publicly available datasets. We confirm that the choice of $\Phi$ and $\epsilon$ is indeed pivotal. With $\Phi$ chosen such that the reductions happen over a single batch (and class) element and with a negligible $\epsilon$, the Dice loss deals with missing labels naturally and performs similarly compared to recent adaptations specific for missing labels. With $\Phi$ chosen such that the reductions happen over multiple batch elements or with a heuristic value for $\epsilon$, the Dice loss handles empty labels correctly. We believe that this work highlights some essential perspectives and hope that it encourages researchers to better describe their exact implementation of the Dice loss in future work.

Shape constrained CNN for segmentation guided prediction of myocardial shape and pose parameters in cardiac MRI

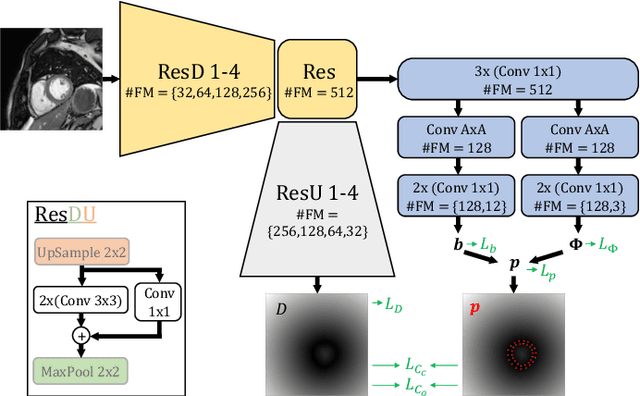
Semantic segmentation using convolutional neural networks (CNNs) is the state-of-the-art for many medical image segmentation tasks including myocardial segmentation in cardiac MR images. However, the predicted segmentation maps obtained from such standard CNN do not allow direct quantification of regional shape properties such as regional wall thickness. Furthermore, the CNNs lack explicit shape constraints, occasionally resulting in unrealistic segmentations. In this paper, we use a CNN to predict shape parameters of an underlying statistical shape model of the myocardium learned from a training set of images. Additionally, the cardiac pose is predicted, which allows to reconstruct the myocardial contours. The integrated shape model regularizes the predicted contours and guarantees realistic shapes. We enforce robustness of shape and pose prediction by simultaneously performing pixel-wise semantic segmentation during training and define two loss functions to impose consistency between the two predicted representations: one distance-based loss and one overlap-based loss. We evaluated the proposed method in a 5-fold cross validation on an in-house clinical dataset with 75 subjects and on the ACDC and LVQuan19 public datasets. We show the benefits of simultaneous semantic segmentation and the two newly defined loss functions for the prediction of shape parameters. Our method achieved a correlation of 99% for left ventricular (LV) area on the three datasets, between 91% and 97% for myocardial area, 98-99% for LV dimensions and between 80% and 92% for regional wall thickness.

Factorizer: A Scalable Interpretable Approach to Context Modeling for Medical Image Segmentation

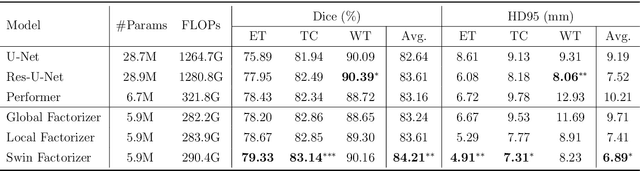
Convolutional Neural Networks (CNNs) with U-shaped architectures have dominated medical image segmentation, which is crucial for various clinical purposes. However, the inherent locality of convolution makes CNNs fail to fully exploit global context, essential for better recognition of some structures, e.g., brain lesions. Transformers have recently proved promising performance on vision tasks, including semantic segmentation, mainly due to their capability of modeling long-range dependencies. Nevertheless, the quadratic complexity of attention makes existing Transformer-based models use self-attention layers only after somehow reducing the image resolution, which limits the ability to capture global contexts present at higher resolutions. Therefore, this work introduces a family of models, dubbed Factorizer, which leverages the power of low-rank matrix factorization for constructing an end-to-end segmentation model. Specifically, we propose a linearly scalable approach to context modeling, formulating Nonnegative Matrix Factorization (NMF) as a differentiable layer integrated into a U-shaped architecture. The shifted window technique is also utilized in combination with NMF to effectively aggregate local information. Factorizers compete favorably with CNNs and Transformers in terms of accuracy, scalability, and interpretability, achieving state-of-the-art results on the BraTS dataset for brain tumor segmentation, with Dice scores of 79.33%, 83.14%, and 90.16% for enhancing tumor, tumor core, and whole tumor, respectively. Highly meaningful NMF components give an additional interpretability advantage to Factorizers over CNNs and Transformers. Moreover, our ablation studies reveal a distinctive feature of Factorizers that enables a significant speed-up in inference for a trained Factorizer without any extra steps and without sacrificing much accuracy.

On the relationship between calibrated predictors and unbiased volume estimation

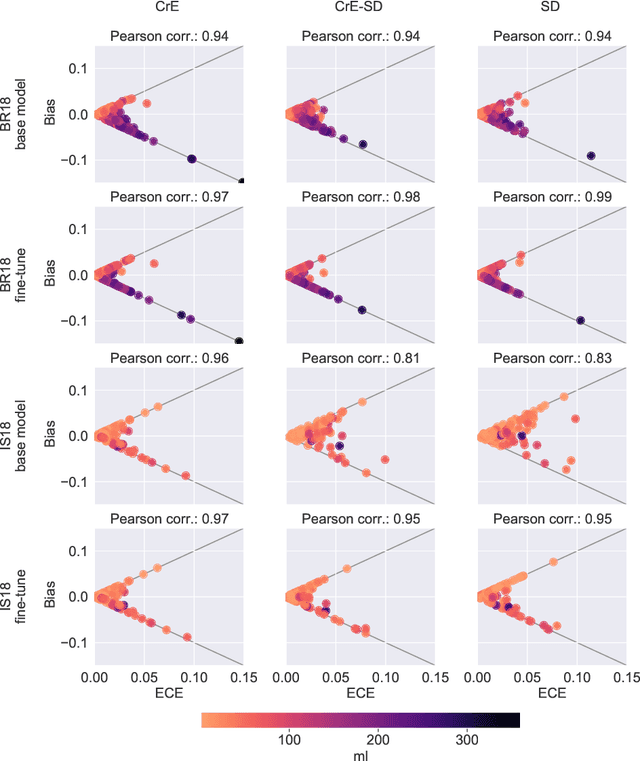
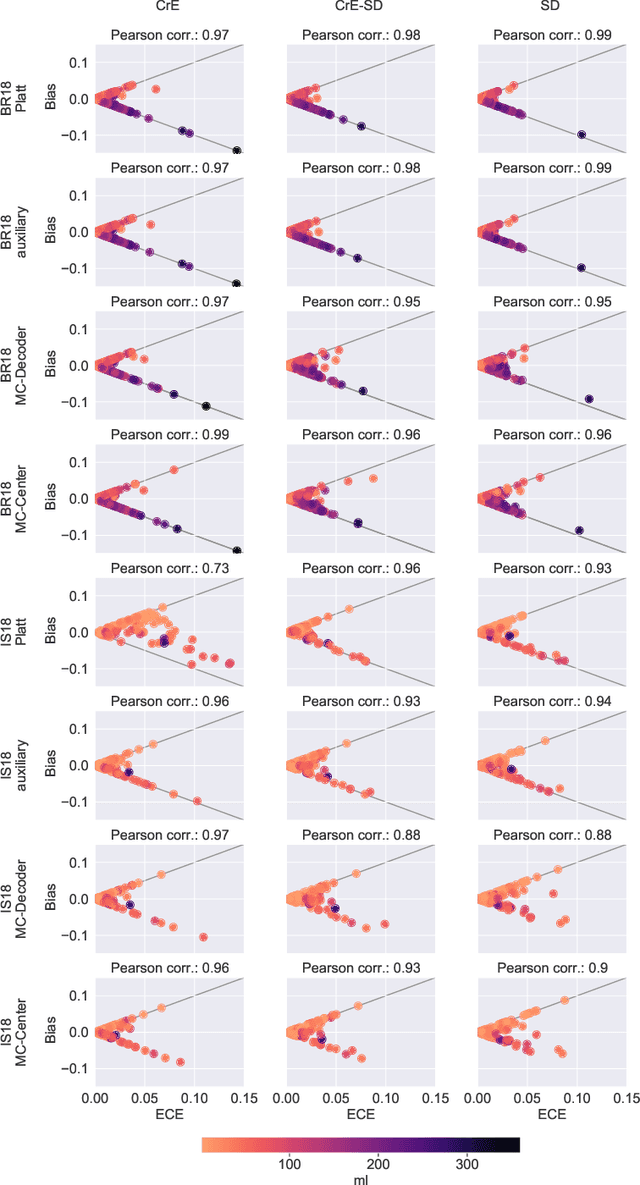
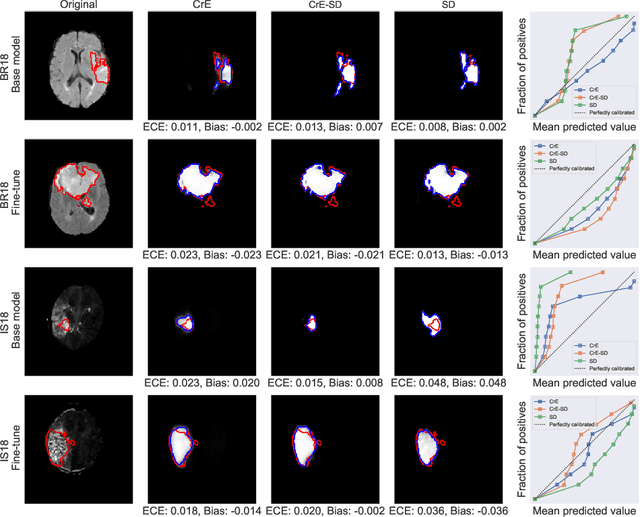
Machine learning driven medical image segmentation has become standard in medical image analysis. However, deep learning models are prone to overconfident predictions. This has led to a renewed focus on calibrated predictions in the medical imaging and broader machine learning communities. Calibrated predictions are estimates of the probability of a label that correspond to the true expected value of the label conditioned on the confidence. Such calibrated predictions have utility in a range of medical imaging applications, including surgical planning under uncertainty and active learning systems. At the same time it is often an accurate volume measurement that is of real importance for many medical applications. This work investigates the relationship between model calibration and volume estimation. We demonstrate both mathematically and empirically that if the predictor is calibrated per image, we can obtain the correct volume by taking an expectation of the probability scores per pixel/voxel of the image. Furthermore, we show that convex combinations of calibrated classifiers preserve volume estimation, but do not preserve calibration. Therefore, we conclude that having a calibrated predictor is a sufficient, but not necessary condition for obtaining an unbiased estimate of the volume. We validate our theoretical findings empirically on a collection of 18 different (calibrated) training strategies on the tasks of glioma volume estimation on BraTS 2018, and ischemic stroke lesion volume estimation on ISLES 2018 datasets.

Explainable-by-design Semi-Supervised Representation Learning for COVID-19 Diagnosis from CT Imaging

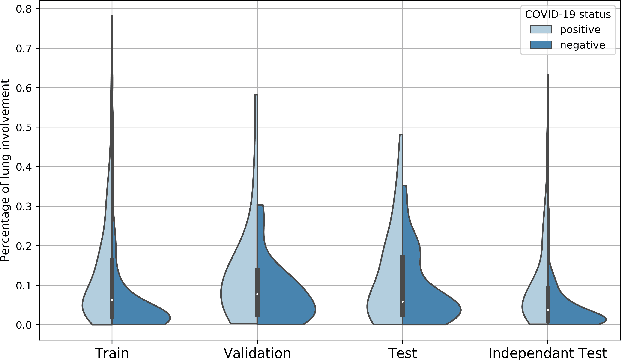
Our motivating application is a real-world problem: COVID-19 classification from CT imaging, for which we present an explainable Deep Learning approach based on a semi-supervised classification pipeline that employs variational autoencoders to extract efficient feature embedding. We have optimized the architecture of two different networks for CT images: (i) a novel conditional variational autoencoder (CVAE) with a specific architecture that integrates the class labels inside the encoder layers and uses side information with shared attention layers for the encoder, which make the most of the contextual clues for representation learning, and (ii) a downstream convolutional neural network for supervised classification using the encoder structure of the CVAE. With the explainable classification results, the proposed diagnosis system is very effective for COVID-19 classification. Based on the promising results obtained qualitatively and quantitatively, we envisage a wide deployment of our developed technique in large-scale clinical studies.Code is available at https://git.etrovub.be/AVSP/ct-based-covid-19-diagnostic-tool.git.

Optimization for Medical Image Segmentation: Theory and Practice when evaluating with Dice Score or Jaccard Index

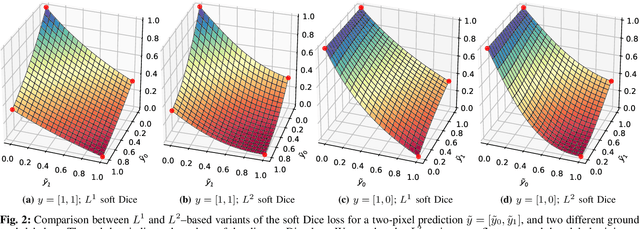
In many medical imaging and classical computer vision tasks, the Dice score and Jaccard index are used to evaluate the segmentation performance. Despite the existence and great empirical success of metric-sensitive losses, i.e. relaxations of these metrics such as soft Dice, soft Jaccard and Lovasz-Softmax, many researchers still use per-pixel losses, such as (weighted) cross-entropy to train CNNs for segmentation. Therefore, the target metric is in many cases not directly optimized. We investigate from a theoretical perspective, the relation within the group of metric-sensitive loss functions and question the existence of an optimal weighting scheme for weighted cross-entropy to optimize the Dice score and Jaccard index at test time. We find that the Dice score and Jaccard index approximate each other relatively and absolutely, but we find no such approximation for a weighted Hamming similarity. For the Tversky loss, the approximation gets monotonically worse when deviating from the trivial weight setting where soft Tversky equals soft Dice. We verify these results empirically in an extensive validation on six medical segmentation tasks and can confirm that metric-sensitive losses are superior to cross-entropy based loss functions in case of evaluation with Dice Score or Jaccard Index. This further holds in a multi-class setting, and across different object sizes and foreground/background ratios. These results encourage a wider adoption of metric-sensitive loss functions for medical segmentation tasks where the performance measure of interest is the Dice score or Jaccard index.

Shape Constrained CNN for Cardiac MR Segmentation with Simultaneous Prediction of Shape and Pose Parameters

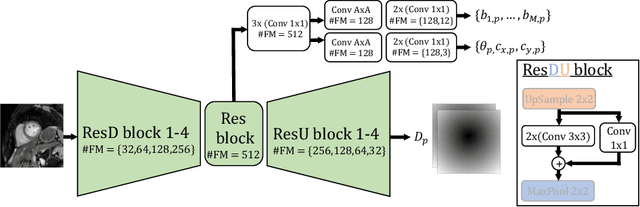
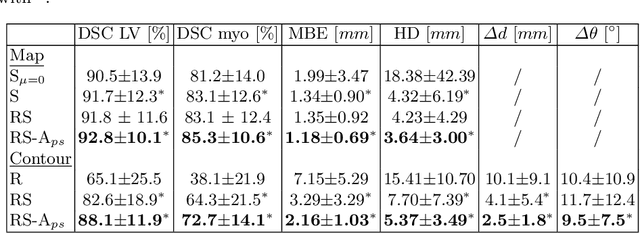
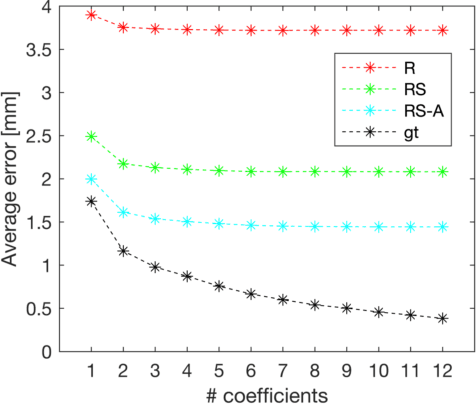
Semantic segmentation using convolutional neural networks (CNNs) is the state-of-the-art for many medical segmentation tasks including left ventricle (LV) segmentation in cardiac MR images. However, a drawback is that these CNNs lack explicit shape constraints, occasionally resulting in unrealistic segmentations. In this paper, we perform LV and myocardial segmentation by regression of pose and shape parameters derived from a statistical shape model. The integrated shape model regularizes predicted segmentations and guarantees realistic shapes. Furthermore, in contrast to semantic segmentation, it allows direct calculation of regional measures such as myocardial thickness. We enforce robustness of shape and pose prediction by simultaneously constructing a segmentation distance map during training. We evaluated the proposed method in a fivefold cross validation on a in-house clinical dataset with 75 subjects containing a total of 1539 delineated short-axis slices covering LV from apex to base, and achieved a correlation of 99% for LV area, 94% for myocardial area, 98% for LV dimensions and 88% for regional wall thicknesses. The method was additionally validated on the LVQuan18 and LVQuan19 public datasets and achieved state-of-the-art results.

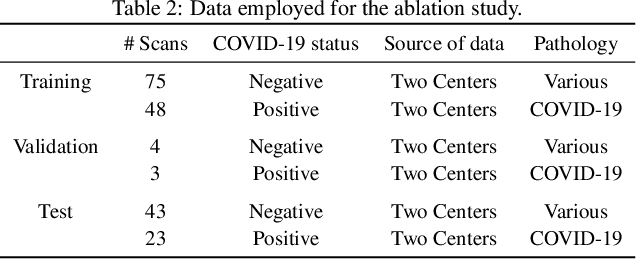
Comparative study of deep learning methods for the automatic segmentation of lung, lesion and lesion type in CT scans of COVID-19 patients

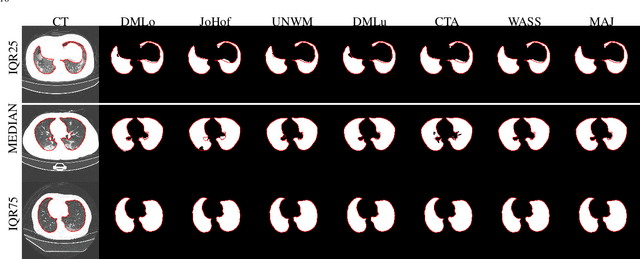
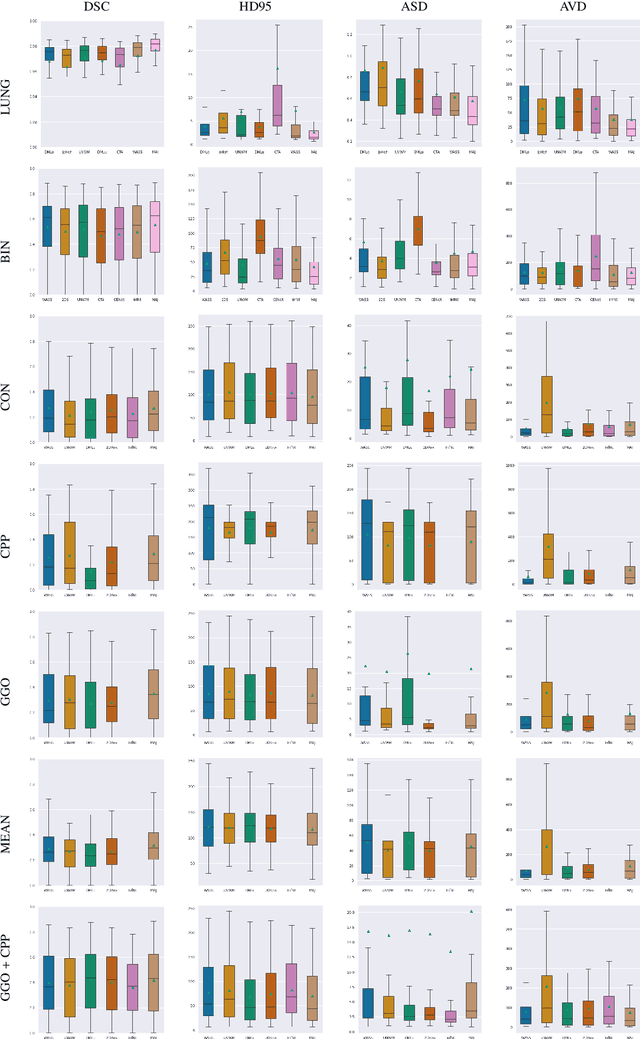
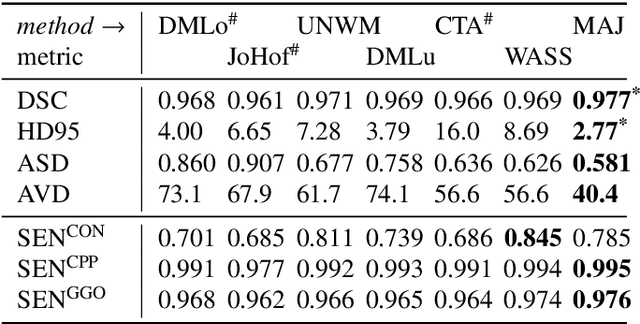
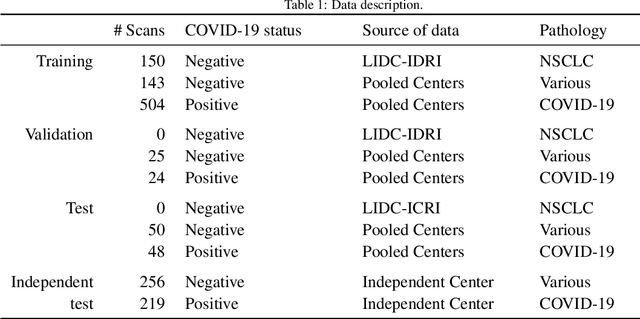
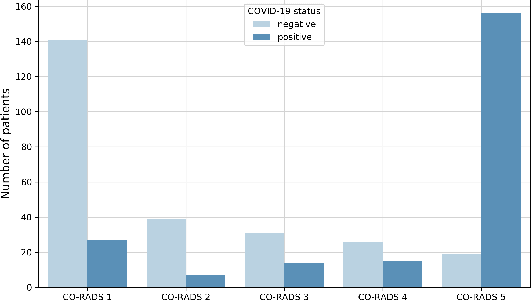
Recent research on COVID-19 suggests that CT imaging provides useful information to assess disease progression and assist diagnosis, in addition to help understanding the disease. There is an increasing number of studies that propose to use deep learning to provide fast and accurate quantification of COVID-19 using chest CT scans. The main tasks of interest are the automatic segmentation of lung and lung lesions in chest CT scans of confirmed or suspected COVID-19 patients. In this study, we compare twelve deep learning algorithms using a multi-center dataset, including both open-source and in-house developed algorithms. Results show that ensembling different methods can boost the overall test set performance for lung segmentation, binary lesion segmentation and multiclass lesion segmentation, resulting in mean Dice scores of 0.982, 0.724 and 0.469, respectively. The resulting binary lesions were segmented with a mean absolute volume error of 91.3 ml. In general, the task of distinguishing different lesion types was more difficult, with a mean absolute volume difference of 152 ml and mean Dice scores of 0.369 and 0.523 for consolidation and ground glass opacity, respectively. All methods perform binary lesion segmentation with an average volume error that is better than visual assessment by human raters, suggesting these methods are mature enough for a large-scale evaluation for use in clinical practice.

Optimizing the Dice Score and Jaccard Index for Medical Image Segmentation: Theory & Practice

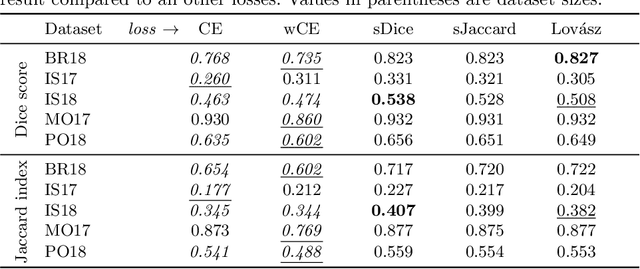
The Dice score and Jaccard index are commonly used metrics for the evaluation of segmentation tasks in medical imaging. Convolutional neural networks trained for image segmentation tasks are usually optimized for (weighted) cross-entropy. This introduces an adverse discrepancy between the learning optimization objective (the loss) and the end target metric. Recent works in computer vision have proposed soft surrogates to alleviate this discrepancy and directly optimize the desired metric, either through relaxations (soft-Dice, soft-Jaccard) or submodular optimization (Lov\'asz-softmax). The aim of this study is two-fold. First, we investigate the theoretical differences in a risk minimization framework and question the existence of a weighted cross-entropy loss with weights theoretically optimized to surrogate Dice or Jaccard. Second, we empirically investigate the behavior of the aforementioned loss functions w.r.t. evaluation with Dice score and Jaccard index on five medical segmentation tasks. Through the application of relative approximation bounds, we show that all surrogates are equivalent up to a multiplicative factor, and that no optimal weighting of cross-entropy exists to approximate Dice or Jaccard measures. We validate these findings empirically and show that, while it is important to opt for one of the target metric surrogates rather than a cross-entropy-based loss, the choice of the surrogate does not make a statistical difference on a wide range of medical segmentation tasks.