Optimizing the Dice Score and Jaccard Index for Medical Image Segmentation: Theory & Practice
Paper and Code
Nov 05, 2019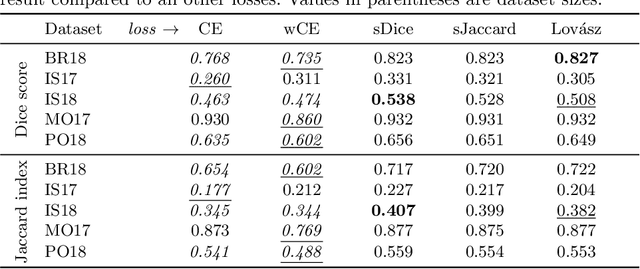

The Dice score and Jaccard index are commonly used metrics for the evaluation of segmentation tasks in medical imaging. Convolutional neural networks trained for image segmentation tasks are usually optimized for (weighted) cross-entropy. This introduces an adverse discrepancy between the learning optimization objective (the loss) and the end target metric. Recent works in computer vision have proposed soft surrogates to alleviate this discrepancy and directly optimize the desired metric, either through relaxations (soft-Dice, soft-Jaccard) or submodular optimization (Lov\'asz-softmax). The aim of this study is two-fold. First, we investigate the theoretical differences in a risk minimization framework and question the existence of a weighted cross-entropy loss with weights theoretically optimized to surrogate Dice or Jaccard. Second, we empirically investigate the behavior of the aforementioned loss functions w.r.t. evaluation with Dice score and Jaccard index on five medical segmentation tasks. Through the application of relative approximation bounds, we show that all surrogates are equivalent up to a multiplicative factor, and that no optimal weighting of cross-entropy exists to approximate Dice or Jaccard measures. We validate these findings empirically and show that, while it is important to opt for one of the target metric surrogates rather than a cross-entropy-based loss, the choice of the surrogate does not make a statistical difference on a wide range of medical segmentation tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge