Explainable-by-design Semi-Supervised Representation Learning for COVID-19 Diagnosis from CT Imaging

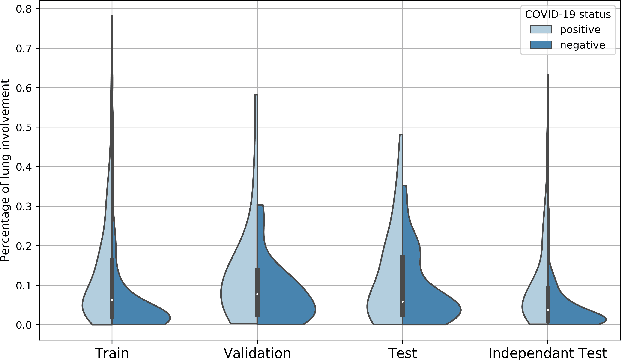
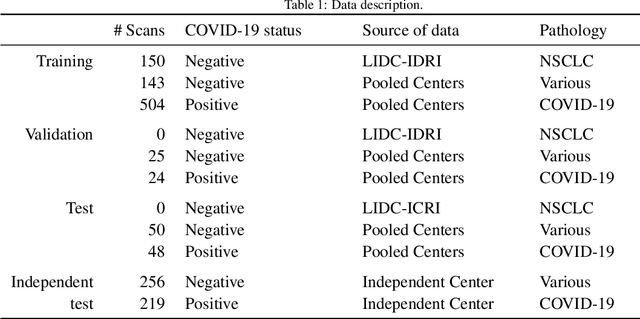
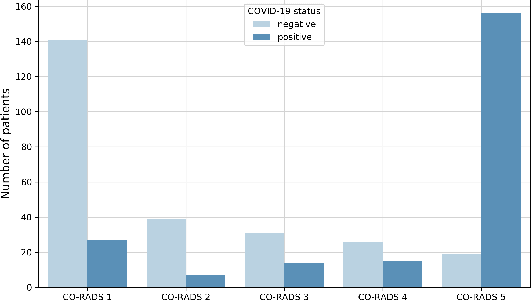
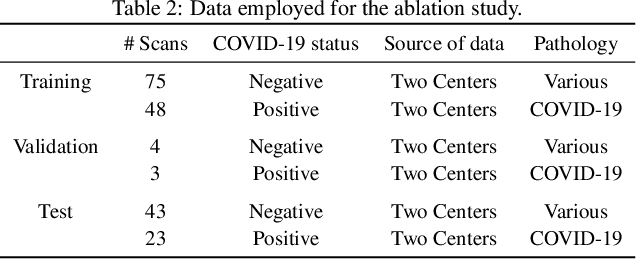
Our motivating application is a real-world problem: COVID-19 classification from CT imaging, for which we present an explainable Deep Learning approach based on a semi-supervised classification pipeline that employs variational autoencoders to extract efficient feature embedding. We have optimized the architecture of two different networks for CT images: (i) a novel conditional variational autoencoder (CVAE) with a specific architecture that integrates the class labels inside the encoder layers and uses side information with shared attention layers for the encoder, which make the most of the contextual clues for representation learning, and (ii) a downstream convolutional neural network for supervised classification using the encoder structure of the CVAE. With the explainable classification results, the proposed diagnosis system is very effective for COVID-19 classification. Based on the promising results obtained qualitatively and quantitatively, we envisage a wide deployment of our developed technique in large-scale clinical studies.Code is available at https://git.etrovub.be/AVSP/ct-based-covid-19-diagnostic-tool.git.

Optimization for Medical Image Segmentation: Theory and Practice when evaluating with Dice Score or Jaccard Index

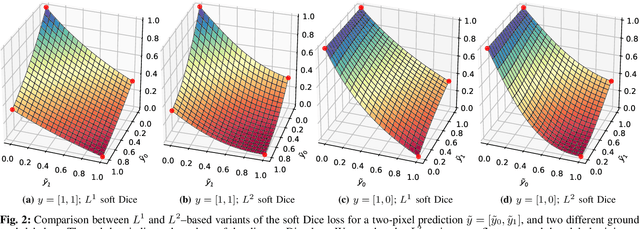
In many medical imaging and classical computer vision tasks, the Dice score and Jaccard index are used to evaluate the segmentation performance. Despite the existence and great empirical success of metric-sensitive losses, i.e. relaxations of these metrics such as soft Dice, soft Jaccard and Lovasz-Softmax, many researchers still use per-pixel losses, such as (weighted) cross-entropy to train CNNs for segmentation. Therefore, the target metric is in many cases not directly optimized. We investigate from a theoretical perspective, the relation within the group of metric-sensitive loss functions and question the existence of an optimal weighting scheme for weighted cross-entropy to optimize the Dice score and Jaccard index at test time. We find that the Dice score and Jaccard index approximate each other relatively and absolutely, but we find no such approximation for a weighted Hamming similarity. For the Tversky loss, the approximation gets monotonically worse when deviating from the trivial weight setting where soft Tversky equals soft Dice. We verify these results empirically in an extensive validation on six medical segmentation tasks and can confirm that metric-sensitive losses are superior to cross-entropy based loss functions in case of evaluation with Dice Score or Jaccard Index. This further holds in a multi-class setting, and across different object sizes and foreground/background ratios. These results encourage a wider adoption of metric-sensitive loss functions for medical segmentation tasks where the performance measure of interest is the Dice score or Jaccard index.

Comparative study of deep learning methods for the automatic segmentation of lung, lesion and lesion type in CT scans of COVID-19 patients

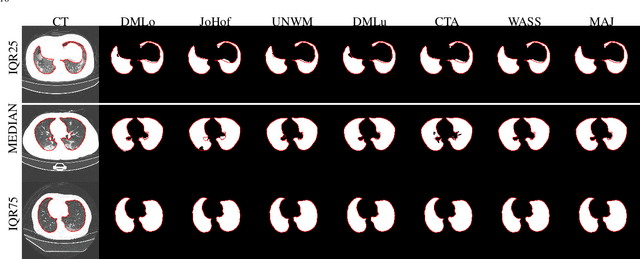
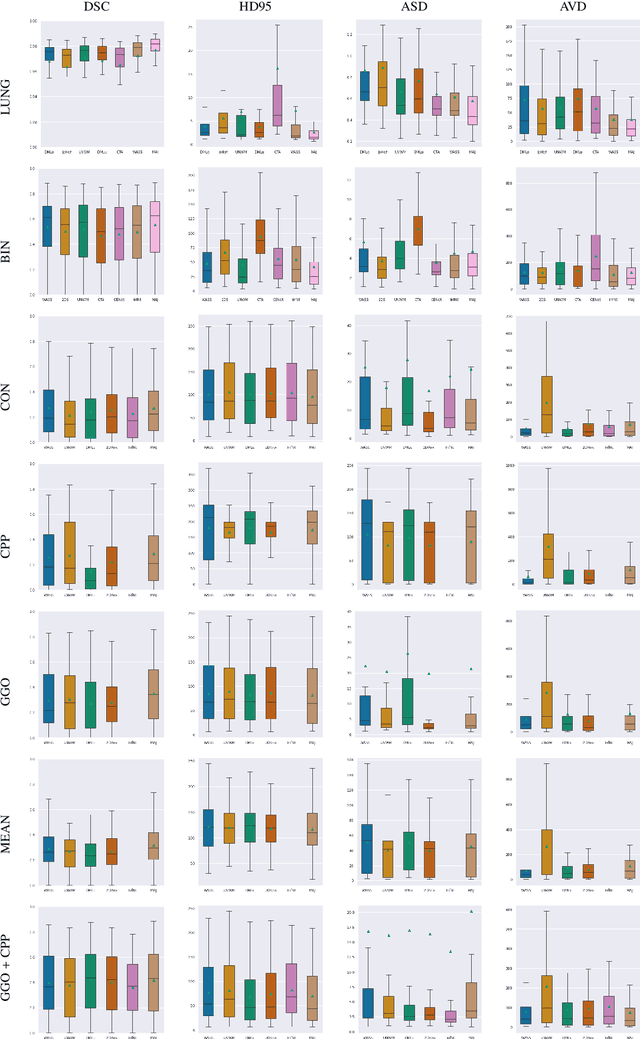
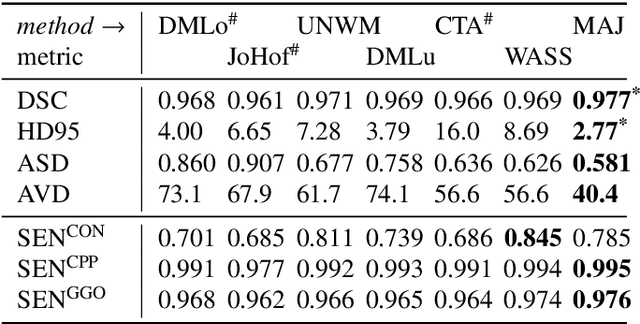
Recent research on COVID-19 suggests that CT imaging provides useful information to assess disease progression and assist diagnosis, in addition to help understanding the disease. There is an increasing number of studies that propose to use deep learning to provide fast and accurate quantification of COVID-19 using chest CT scans. The main tasks of interest are the automatic segmentation of lung and lung lesions in chest CT scans of confirmed or suspected COVID-19 patients. In this study, we compare twelve deep learning algorithms using a multi-center dataset, including both open-source and in-house developed algorithms. Results show that ensembling different methods can boost the overall test set performance for lung segmentation, binary lesion segmentation and multiclass lesion segmentation, resulting in mean Dice scores of 0.982, 0.724 and 0.469, respectively. The resulting binary lesions were segmented with a mean absolute volume error of 91.3 ml. In general, the task of distinguishing different lesion types was more difficult, with a mean absolute volume difference of 152 ml and mean Dice scores of 0.369 and 0.523 for consolidation and ground glass opacity, respectively. All methods perform binary lesion segmentation with an average volume error that is better than visual assessment by human raters, suggesting these methods are mature enough for a large-scale evaluation for use in clinical practice.

Optimizing the Dice Score and Jaccard Index for Medical Image Segmentation: Theory & Practice

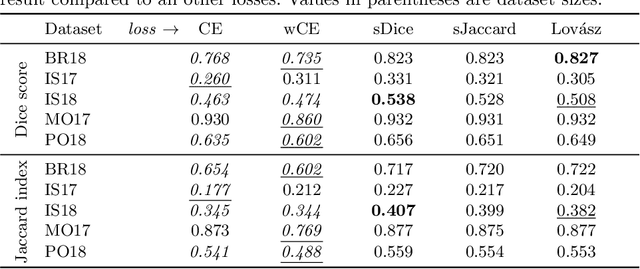
The Dice score and Jaccard index are commonly used metrics for the evaluation of segmentation tasks in medical imaging. Convolutional neural networks trained for image segmentation tasks are usually optimized for (weighted) cross-entropy. This introduces an adverse discrepancy between the learning optimization objective (the loss) and the end target metric. Recent works in computer vision have proposed soft surrogates to alleviate this discrepancy and directly optimize the desired metric, either through relaxations (soft-Dice, soft-Jaccard) or submodular optimization (Lov\'asz-softmax). The aim of this study is two-fold. First, we investigate the theoretical differences in a risk minimization framework and question the existence of a weighted cross-entropy loss with weights theoretically optimized to surrogate Dice or Jaccard. Second, we empirically investigate the behavior of the aforementioned loss functions w.r.t. evaluation with Dice score and Jaccard index on five medical segmentation tasks. Through the application of relative approximation bounds, we show that all surrogates are equivalent up to a multiplicative factor, and that no optimal weighting of cross-entropy exists to approximate Dice or Jaccard measures. We validate these findings empirically and show that, while it is important to opt for one of the target metric surrogates rather than a cross-entropy-based loss, the choice of the surrogate does not make a statistical difference on a wide range of medical segmentation tasks.