Revisiting Evaluation Metrics for Semantic Segmentation: Optimization and Evaluation of Fine-grained Intersection over Union

Semantic segmentation datasets often exhibit two types of imbalance: \textit{class imbalance}, where some classes appear more frequently than others and \textit{size imbalance}, where some objects occupy more pixels than others. This causes traditional evaluation metrics to be biased towards \textit{majority classes} (e.g. overall pixel-wise accuracy) and \textit{large objects} (e.g. mean pixel-wise accuracy and per-dataset mean intersection over union). To address these shortcomings, we propose the use of fine-grained mIoUs along with corresponding worst-case metrics, thereby offering a more holistic evaluation of segmentation techniques. These fine-grained metrics offer less bias towards large objects, richer statistical information, and valuable insights into model and dataset auditing. Furthermore, we undertake an extensive benchmark study, where we train and evaluate 15 modern neural networks with the proposed metrics on 12 diverse natural and aerial segmentation datasets. Our benchmark study highlights the necessity of not basing evaluations on a single metric and confirms that fine-grained mIoUs reduce the bias towards large objects. Moreover, we identify the crucial role played by architecture designs and loss functions, which lead to best practices in optimizing fine-grained metrics. The code is available at \href{https://github.com/zifuwanggg/JDTLosses}{https://github.com/zifuwanggg/JDTLosses}.

Spatial Consistency Loss for Training Multi-Label Classifiers from Single-Label Annotations

As natural images usually contain multiple objects, multi-label image classification is more applicable "in the wild" than single-label classification. However, exhaustively annotating images with every object of interest is costly and time-consuming. We aim to train multi-label classifiers from single-label annotations only. We show that adding a consistency loss, ensuring that the predictions of the network are consistent over consecutive training epochs, is a simple yet effective method to train multi-label classifiers in a weakly supervised setting. We further extend this approach spatially, by ensuring consistency of the spatial feature maps produced over consecutive training epochs, maintaining per-class running-average heatmaps for each training image. We show that this spatial consistency loss further improves the multi-label mAP of the classifiers. In addition, we show that this method overcomes shortcomings of the "crop" data-augmentation by recovering correct supervision signal even when most of the single ground truth object is cropped out of the input image by the data augmentation. We demonstrate gains of the consistency and spatial consistency losses over the binary cross-entropy baseline, and over competing methods, on MS-COCO and Pascal VOC. We also demonstrate improved multi-label classification mAP on ImageNet-1K using the ReaL multi-label validation set.

Optimization for Medical Image Segmentation: Theory and Practice when evaluating with Dice Score or Jaccard Index

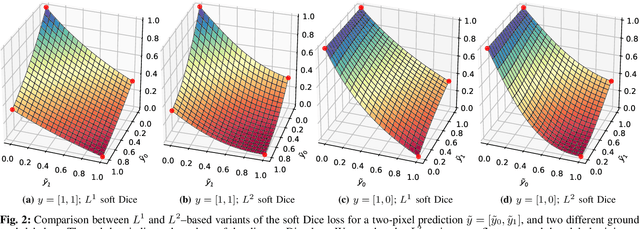
In many medical imaging and classical computer vision tasks, the Dice score and Jaccard index are used to evaluate the segmentation performance. Despite the existence and great empirical success of metric-sensitive losses, i.e. relaxations of these metrics such as soft Dice, soft Jaccard and Lovasz-Softmax, many researchers still use per-pixel losses, such as (weighted) cross-entropy to train CNNs for segmentation. Therefore, the target metric is in many cases not directly optimized. We investigate from a theoretical perspective, the relation within the group of metric-sensitive loss functions and question the existence of an optimal weighting scheme for weighted cross-entropy to optimize the Dice score and Jaccard index at test time. We find that the Dice score and Jaccard index approximate each other relatively and absolutely, but we find no such approximation for a weighted Hamming similarity. For the Tversky loss, the approximation gets monotonically worse when deviating from the trivial weight setting where soft Tversky equals soft Dice. We verify these results empirically in an extensive validation on six medical segmentation tasks and can confirm that metric-sensitive losses are superior to cross-entropy based loss functions in case of evaluation with Dice Score or Jaccard Index. This further holds in a multi-class setting, and across different object sizes and foreground/background ratios. These results encourage a wider adoption of metric-sensitive loss functions for medical segmentation tasks where the performance measure of interest is the Dice score or Jaccard index.

AOWS: Adaptive and optimal network width search with latency constraints

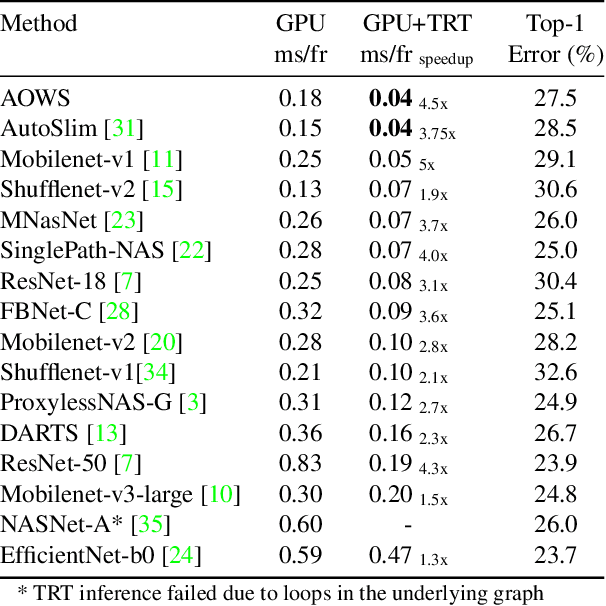
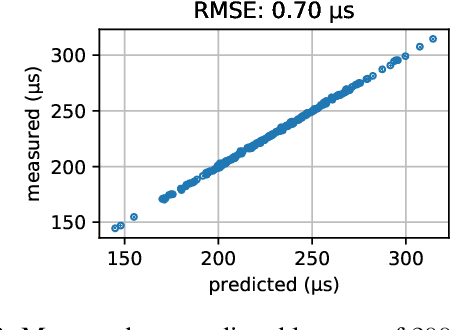
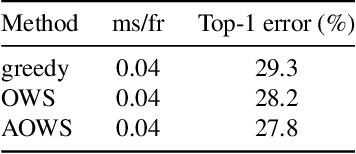
Neural architecture search (NAS) approaches aim at automatically finding novel CNN architectures that fit computational constraints while maintaining a good performance on the target platform. We introduce a novel efficient one-shot NAS approach to optimally search for channel numbers, given latency constraints on a specific hardware. We first show that we can use a black-box approach to estimate a realistic latency model for a specific inference platform, without the need for low-level access to the inference computation. Then, we design a pairwise MRF to score any channel configuration and use dynamic programming to efficiently decode the best performing configuration, yielding an optimal solution for the network width search. Finally, we propose an adaptive channel configuration sampling scheme to gradually specialize the training phase to the target computational constraints. Experiments on ImageNet classification show that our approach can find networks fitting the resource constraints on different target platforms while improving accuracy over the state-of-the-art efficient networks.

Discriminative training of conditional random fields with probably submodular constraints

Problems of segmentation, denoising, registration and 3D reconstruction are often addressed with the graph cut algorithm. However, solving an unconstrained graph cut problem is NP-hard. For tractable optimization, pairwise potentials have to fulfill the submodularity inequality. In our learning paradigm, pairwise potentials are created as the dot product of a learned vector w with positive feature vectors. In order to constrain such a model to remain tractable, previous approaches have enforced the weight vector to be positive for pairwise potentials in which the labels differ, and set pairwise potentials to zero in the case that the label remains the same. Such constraints are sufficient to guarantee that the resulting pairwise potentials satisfy the submodularity inequality. However, we show that such an approach unnecessarily restricts the capacity of the learned models. Guaranteeing submodularity for all possible inputs, no matter how improbable, reduces inference error to effectively zero, but increases model error. In contrast, we relax the requirement of guaranteed submodularity to solutions that are probably approximately submodular. We show that the conceptually simple strategy of enforcing submodularity on the training examples guarantees with low sample complexity that test images will also yield submodular pairwise potentials. Results are presented in the binary and muticlass settings, showing substantial improvement from the resulting increased model capacity.

Optimizing the Dice Score and Jaccard Index for Medical Image Segmentation: Theory & Practice

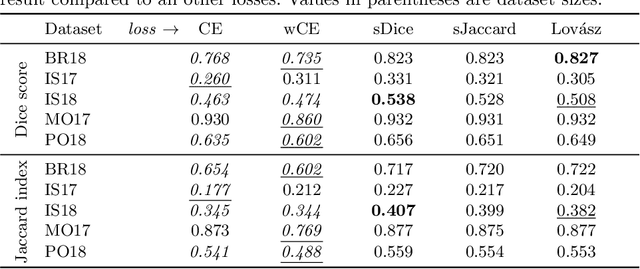
The Dice score and Jaccard index are commonly used metrics for the evaluation of segmentation tasks in medical imaging. Convolutional neural networks trained for image segmentation tasks are usually optimized for (weighted) cross-entropy. This introduces an adverse discrepancy between the learning optimization objective (the loss) and the end target metric. Recent works in computer vision have proposed soft surrogates to alleviate this discrepancy and directly optimize the desired metric, either through relaxations (soft-Dice, soft-Jaccard) or submodular optimization (Lov\'asz-softmax). The aim of this study is two-fold. First, we investigate the theoretical differences in a risk minimization framework and question the existence of a weighted cross-entropy loss with weights theoretically optimized to surrogate Dice or Jaccard. Second, we empirically investigate the behavior of the aforementioned loss functions w.r.t. evaluation with Dice score and Jaccard index on five medical segmentation tasks. Through the application of relative approximation bounds, we show that all surrogates are equivalent up to a multiplicative factor, and that no optimal weighting of cross-entropy exists to approximate Dice or Jaccard measures. We validate these findings empirically and show that, while it is important to opt for one of the target metric surrogates rather than a cross-entropy-based loss, the choice of the surrogate does not make a statistical difference on a wide range of medical segmentation tasks.

Adaptive Compression-based Lifelong Learning

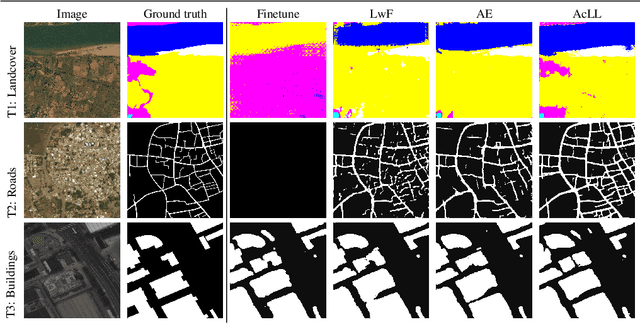
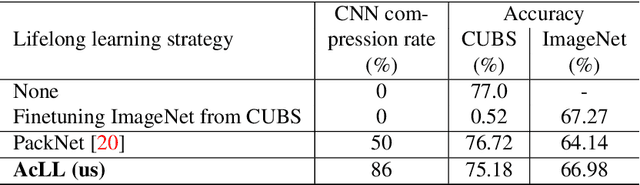
The problem of a deep learning model losing performance on a previously learned task when fine-tuned to a new one is a phenomenon known as Catastrophic forgetting. There are two major ways to mitigate this problem: either preserving activations of the initial network during training with a new task; or restricting the new network activations to remain close to the initial ones. The latter approach falls under the denomination of lifelong learning, where the model is updated in a way that it performs well on both old and new tasks, without having access to the old task's training samples anymore. Recently, approaches like pruning networks for freeing network capacity during sequential learning of tasks have been gaining in popularity. Such approaches allow learning small networks while making redundant parameters available for the next tasks. The common problem encountered with these approaches is that the pruning percentage is hard-coded, irrespective of the number of samples, of the complexity of the learning task and of the number of classes in the dataset. We propose a method based on Bayesian optimization to perform adaptive compression/pruning of the network and show its effectiveness in lifelong learning. Our method learns to perform heavy pruning for small and/or simple datasets while using milder compression rates for large and/or complex data. Experiments on classification and semantic segmentation demonstrate the applicability of learning network compression, where we are able to effectively preserve performances along sequences of tasks of varying complexity.

MultiGrain: a unified image embedding for classes and instances

MultiGrain is a network architecture producing compact vector representations that are suited both for image classification and particular object retrieval. It builds on a standard classification trunk. The top of the network produces an embedding containing coarse and fine-grained information, so that images can be recognized based on the object class, particular object, or if they are distorted copies. Our joint training is simple: we minimize a cross-entropy loss for classification and a ranking loss that determines if two images are identical up to data augmentation, with no need for additional labels. A key component of MultiGrain is a pooling layer that takes advantage of high-resolution images with a network trained at a lower resolution. When fed to a linear classifier, the learned embeddings provide state-of-the-art classification accuracy. For instance, we obtain 79.4% top-1 accuracy with a ResNet-50 learned on Imagenet, which is a +1.8% absolute improvement over the AutoAugment method. When compared with the cosine similarity, the same embeddings perform on par with the state-of-the-art for image retrieval at moderate resolutions.

Generating superpixels using deep image representations

Superpixel algorithms are a common pre-processing step for computer vision algorithms such as segmentation, object tracking and localization. Many superpixel methods only rely on colors features for segmentation, limiting performance in low-contrast regions and applicability to infrared or medical images where object boundaries have wide appearance variability. We study the inclusion of deep image features in the SLIC superpixel algorithm to exploit higher-level image representations. In addition, we devise a trainable superpixel algorithm, yielding an intermediate domain-specific image representation that can be applied to different tasks. A clustering-based superpixel algorithm is transformed into a pixel-wise classification task and superpixel training data is derived from semantic segmentation datasets. Our results demonstrate that this approach is able to improve superpixel quality consistently.

Yes, IoU loss is submodular - as a function of the mispredictions

This note is a response to [7] in which it is claimed that [13, Proposition 11] is false. We demonstrate here that this assertion in [7] is false, and is based on a misreading of the notion of set membership in [13, Proposition 11]. We maintain that [13, Proposition 11] is true. ([7] = arXiv:1809.00593, [13] = arXiv:1512.07797)