Co-VLA: Coordination-Aware Structured Action Modeling for Dual-Arm Vision-Language-Action Systems

Vision-language-action (VLA) models show strong capabilities in single and dual-arm robotic manipulation. Prior works show coordinated bimanual behaviors can emerge from end-to-end learning, leveraging large vision-language backbones with continuous action prediction. However, as bimanual tasks become tightly coupled and execution constraints become critical, implicit coordination alone is insufficient to ensure reliable, interpretable, and stable behavior. In this work, we propose Co-VLA, a coordination-aware bimanual manipulation framework introducing explicit structural priors into VLA models. We instantiate our method on a state-of-the-art vision-language backbone by replacing its monolithic action head with a Structured Action Expert (SAE) designed for bimanual coordination. Specifically, we introduce explicit structure at the action generation level with a modular coordination-aware loss that shapes shared and residual latents according to task-specific structures. The shared latent encodes task-level coordination intent, while residual latents capture execution adjustments for each arm. At deployment, a Latent-Aware Controller (LAC) interprets the learned representations to modulate synchronization strength, execution asymmetry, smoothness, and safety constraints in real time. LAC operates at the joint-command level and remains compatible with standard control pipelines without requiring force or impedance control. Experiments across simulation and real-world benchmarks show Co-VLA significantly outperforms monolithic baselines, achieving a 27% success rate gain in tight-coordination tasks, more than doubling performance in OOD real-world scenarios (from 13% to 27%), and reducing task completion time by up to 25%.

Mem-World: Memory-Augmented Action-Conditioned World Models for Persistent Robot Manipulation

Action-conditioned world models have emerged as a promising paradigm for robot learning, offering a scalable alternative to costly real-world experimentation by generating action-consistent video rollouts. However, persistent world modeling remains challenging in manipulation: frequent end-effector occlusions and rapid wrist-camera motion make the current observation insufficient for predicting future views, causing models to forget or hallucinate scene details seen in earlier frames. Existing memory retrieval strategies often fail to identify informative history in dynamic manipulation scenarios. To address this limitation, we propose Mem-World, a memory-augmented multi-view action-conditioned world model. At its core, we present W-VMem, a 4D wrist-view-centered surfel-indexed memory that anchors historical observations to temporally evolving surface elements. By explicitly modeling when and where scene elements are observed, W-VMem enables geometry-aware retrieval of relevant history frames conditioned on future actions. During generation, relevant history frames are selected via surfel-based rendering and scoring, providing informative and non-redundant context for prediction. Extensive experiments show that Mem-World generates persistent rollouts in complex manipulation scenarios, enables more reliable policy evaluation than Ctrl-World, improving the Pearson correlation with real-world performance by 14.5\%, and supports effective policy improvement through synthetic data generation, increasing success rates from 58\% to 72\% on long-horizon tasks.

DAM-VLA: A Dynamic Action Model-Based Vision-Language-Action Framework for Robot Manipulation

In dynamic environments such as warehouses, hospitals, and homes, robots must seamlessly transition between gross motion and precise manipulations to complete complex tasks. However, current Vision-Language-Action (VLA) frameworks, largely adapted from pre-trained Vision-Language Models (VLMs), often struggle to reconcile general task adaptability with the specialized precision required for intricate manipulation. To address this challenge, we propose DAM-VLA, a dynamic action model-based VLA framework. DAM-VLA integrates VLM reasoning with diffusion-based action models specialized for arm and gripper control. Specifically, it introduces (i) an action routing mechanism, using task-specific visual and linguistic cues to select appropriate action models (e.g., arm movement or gripper manipulation), (ii) a dynamic action model that fuses high-level VLM cognition with low-level visual features to predict actions, and (iii) a dual-scale action weighting mechanism that enables dynamic coordination between the arm-movement and gripper-manipulation models. Across extensive evaluations, DAM-VLA achieves superior success rates compared to state-of-the-art VLA methods in simulated (SIMPLER, FurnitureBench) and real-world settings, showing robust generalization from standard pick-and-place to demanding long-horizon and contact-rich tasks.

MoSE: Skill-by-Skill Mixture-of-Expert Learning for Autonomous Driving

Recent studies show large language models (LLMs) and vision language models (VLMs) trained using web-scale data can empower end-to-end autonomous driving systems for a better generalization and interpretation. Specifically, by dynamically routing inputs to specialized subsets of parameters, the Mixture-of-Experts (MoE) technique enables general LLMs or VLMs to achieve substantial performance improvements while maintaining computational efficiency. However, general MoE models usually demands extensive training data and complex optimization. In this work, inspired by the learning process of human drivers, we propose a skill-oriented MoE, called MoSE, which mimics human drivers' learning process and reasoning process, skill-by-skill and step-by-step. We propose a skill-oriented routing mechanism that begins with defining and annotating specific skills, enabling experts to identify the necessary driving competencies for various scenarios and reasoning tasks, thereby facilitating skill-by-skill learning. Further align the driving process to multi-step planning in human reasoning and end-to-end driving models, we build a hierarchical skill dataset and pretrain the router to encourage the model to think step-by-step. Unlike multi-round dialogs, MoSE integrates valuable auxiliary tasks (e.g.\ description, reasoning, planning) in one single forward process without introducing any extra computational cost. With less than 3B sparsely activated parameters, our model outperforms several 8B+ parameters on CODA AD corner case reasoning task. Compared to existing methods based on open-source models and data, our approach achieves state-of-the-art performance with significantly reduced activated model size (at least by $62.5\%$) with a single-turn conversation.

Jigsaw-R1: A Study of Rule-based Visual Reinforcement Learning with Jigsaw Puzzles

The application of rule-based reinforcement learning (RL) to multimodal large language models (MLLMs) introduces unique challenges and potential deviations from findings in text-only domains, particularly for perception-heavy tasks. This paper provides a comprehensive study of rule-based visual RL using jigsaw puzzles as a structured experimental framework, revealing several key findings. \textit{Firstly,} we find that MLLMs, initially performing near to random guessing on simple puzzles, achieve near-perfect accuracy and generalize to complex, unseen configurations through fine-tuning. \textit{Secondly,} training on jigsaw puzzles can induce generalization to other visual tasks, with effectiveness tied to specific task configurations. \textit{Thirdly,} MLLMs can learn and generalize with or without explicit reasoning, though open-source models often favor direct answering. Consequently, even when trained for step-by-step reasoning, they can ignore the thinking process in deriving the final answer. \textit{Fourthly,} we observe that complex reasoning patterns appear to be pre-existing rather than emergent, with their frequency increasing alongside training and task difficulty. \textit{Finally,} our results demonstrate that RL exhibits more effective generalization than Supervised Fine-Tuning (SFT), and an initial SFT cold start phase can hinder subsequent RL optimization. Although these observations are based on jigsaw puzzles and may vary across other visual tasks, this research contributes a valuable piece of jigsaw to the larger puzzle of collective understanding rule-based visual RL and its potential in multimodal learning. The code is available at: \href{https://github.com/zifuwanggg/Jigsaw-R1}{https://github.com/zifuwanggg/Jigsaw-R1}.

BLADE: Benchmarking Language Model Agents for Data-Driven Science

Data-driven scientific discovery requires the iterative integration of scientific domain knowledge, statistical expertise, and an understanding of data semantics to make nuanced analytical decisions, e.g., about which variables, transformations, and statistical models to consider. LM-based agents equipped with planning, memory, and code execution capabilities have the potential to support data-driven science. However, evaluating agents on such open-ended tasks is challenging due to multiple valid approaches, partially correct steps, and different ways to express the same decisions. To address these challenges, we present BLADE, a benchmark to automatically evaluate agents' multifaceted approaches to open-ended research questions. BLADE consists of 12 datasets and research questions drawn from existing scientific literature, with ground truth collected from independent analyses by expert data scientists and researchers. To automatically evaluate agent responses, we developed corresponding computational methods to match different representations of analyses to this ground truth. Though language models possess considerable world knowledge, our evaluation shows that they are often limited to basic analyses. However, agents capable of interacting with the underlying data demonstrate improved, but still non-optimal, diversity in their analytical decision making. Our work enables the evaluation of agents for data-driven science and provides researchers deeper insights into agents' analysis approaches.

HIMap: HybrId Representation Learning for End-to-end Vectorized HD Map Construction

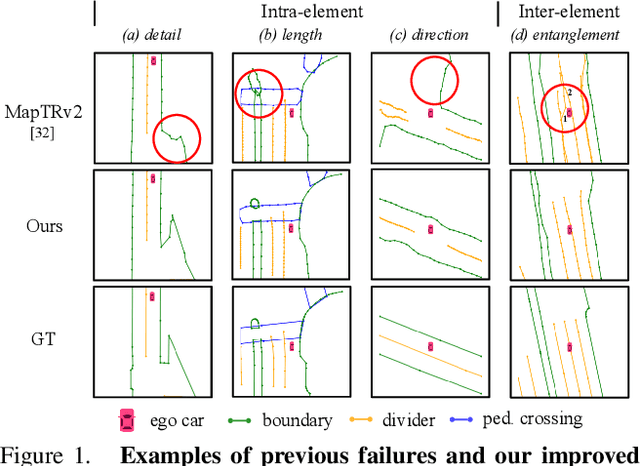
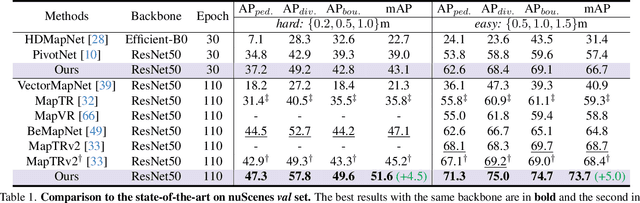
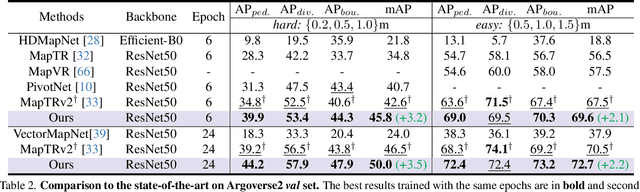
Vectorized High-Definition (HD) map construction requires predictions of the category and point coordinates of map elements (e.g. road boundary, lane divider, pedestrian crossing, etc.). State-of-the-art methods are mainly based on point-level representation learning for regressing accurate point coordinates. However, this pipeline has limitations in obtaining element-level information and handling element-level failures, e.g. erroneous element shape or entanglement between elements. To tackle the above issues, we propose a simple yet effective HybrId framework named HIMap to sufficiently learn and interact both point-level and element-level information. Concretely, we introduce a hybrid representation called HIQuery to represent all map elements, and propose a point-element interactor to interactively extract and encode the hybrid information of elements, e.g. point position and element shape, into the HIQuery. Additionally, we present a point-element consistency constraint to enhance the consistency between the point-level and element-level information. Finally, the output point-element integrated HIQuery can be directly converted into map elements' class, point coordinates, and mask. We conduct extensive experiments and consistently outperform previous methods on both nuScenes and Argoverse2 datasets. Notably, our method achieves $77.8$ mAP on the nuScenes dataset, remarkably superior to previous SOTAs by $8.3$ mAP at least.

Revisiting Evaluation Metrics for Semantic Segmentation: Optimization and Evaluation of Fine-grained Intersection over Union

Semantic segmentation datasets often exhibit two types of imbalance: \textit{class imbalance}, where some classes appear more frequently than others and \textit{size imbalance}, where some objects occupy more pixels than others. This causes traditional evaluation metrics to be biased towards \textit{majority classes} (e.g. overall pixel-wise accuracy) and \textit{large objects} (e.g. mean pixel-wise accuracy and per-dataset mean intersection over union). To address these shortcomings, we propose the use of fine-grained mIoUs along with corresponding worst-case metrics, thereby offering a more holistic evaluation of segmentation techniques. These fine-grained metrics offer less bias towards large objects, richer statistical information, and valuable insights into model and dataset auditing. Furthermore, we undertake an extensive benchmark study, where we train and evaluate 15 modern neural networks with the proposed metrics on 12 diverse natural and aerial segmentation datasets. Our benchmark study highlights the necessity of not basing evaluations on a single metric and confirms that fine-grained mIoUs reduce the bias towards large objects. Moreover, we identify the crucial role played by architecture designs and loss functions, which lead to best practices in optimizing fine-grained metrics. The code is available at \href{https://github.com/zifuwanggg/JDTLosses}{https://github.com/zifuwanggg/JDTLosses}.

Yes, IoU loss is submodular - as a function of the mispredictions

This note is a response to [7] in which it is claimed that [13, Proposition 11] is false. We demonstrate here that this assertion in [7] is false, and is based on a misreading of the notion of set membership in [13, Proposition 11]. We maintain that [13, Proposition 11] is true. ([7] = arXiv:1809.00593, [13] = arXiv:1512.07797)

The Lovász Hinge: A Novel Convex Surrogate for Submodular Losses

Learning with non-modular losses is an important problem when sets of predictions are made simultaneously. The main tools for constructing convex surrogate loss functions for set prediction are margin rescaling and slack rescaling. In this work, we show that these strategies lead to tight convex surrogates iff the underlying loss function is increasing in the number of incorrect predictions. However, gradient or cutting-plane computation for these functions is NP-hard for non-supermodular loss functions. We propose instead a novel surrogate loss function for submodular losses, the Lov\'asz hinge, which leads to O(p log p) complexity with O(p) oracle accesses to the loss function to compute a gradient or cutting-plane. We prove that the Lov\'asz hinge is convex and yields an extension. As a result, we have developed the first tractable convex surrogates in the literature for submodular losses. We demonstrate the utility of this novel convex surrogate through several set prediction tasks, including on the PASCAL VOC and Microsoft COCO datasets.