The Dice loss in the context of missing or empty labels: Introducing $Φ$ and $ε$

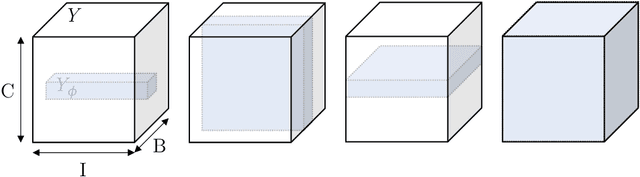
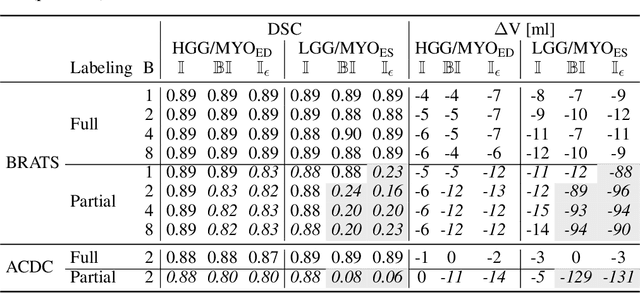
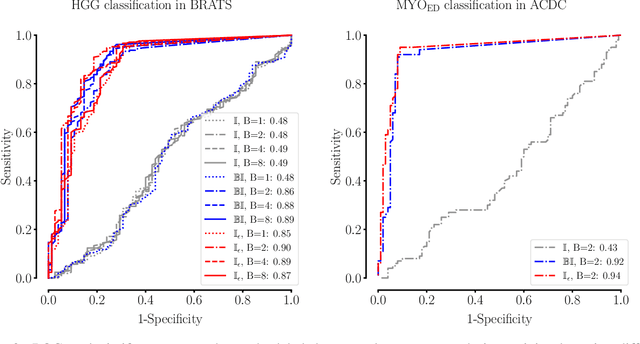
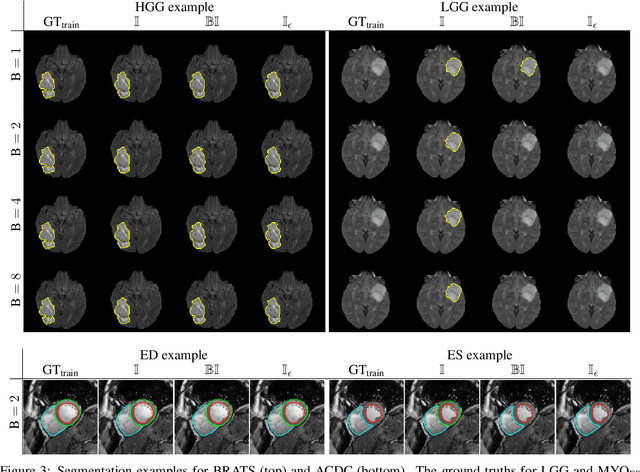
Albeit the Dice loss is one of the dominant loss functions in medical image segmentation, most research omits a closer look at its derivative, i.e. the real motor of the optimization when using gradient descent. In this paper, we highlight the peculiar action of the Dice loss in the presence of missing or empty labels. First, we formulate a theoretical basis that gives a general description of the Dice loss and its derivative. It turns out that the choice of the reduction dimensions $\Phi$ and the smoothing term $\epsilon$ is non-trivial and greatly influences its behavior. We find and propose heuristic combinations of $\Phi$ and $\epsilon$ that work in a segmentation setting with either missing or empty labels. Second, we empirically validate these findings in a binary and multiclass segmentation setting using two publicly available datasets. We confirm that the choice of $\Phi$ and $\epsilon$ is indeed pivotal. With $\Phi$ chosen such that the reductions happen over a single batch (and class) element and with a negligible $\epsilon$, the Dice loss deals with missing labels naturally and performs similarly compared to recent adaptations specific for missing labels. With $\Phi$ chosen such that the reductions happen over multiple batch elements or with a heuristic value for $\epsilon$, the Dice loss handles empty labels correctly. We believe that this work highlights some essential perspectives and hope that it encourages researchers to better describe their exact implementation of the Dice loss in future work.