Revisiting Reweighted Risk for Calibration: AURC, Focal Loss, and Inverse Focal Loss

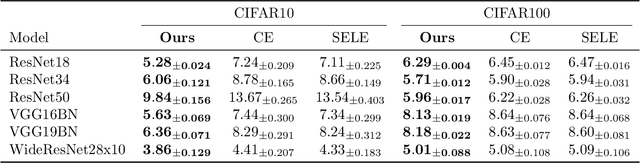
Several variants of reweighted risk functionals, such as focal losss, inverse focal loss, and the Area Under the Risk-Coverage Curve (AURC), have been proposed in the literature and claims have been made in relation to their calibration properties. However, focal loss and inverse focal loss propose vastly different weighting schemes. In this paper, we revisit a broad class of weighted risk functions commonly used in deep learning and establish a principled connection between these reweighting schemes and calibration errors. We show that minimizing calibration error is closely linked to the selective classification paradigm and demonstrate that optimizing a regularized variant of the AURC naturally leads to improved calibration. This regularized AURC shares a similar reweighting strategy with inverse focal loss, lending support to the idea that focal loss is less principled when calibration is a desired outcome. Direct AURC optimization offers greater flexibility through the choice of confidence score functions (CSFs). To enable gradient-based optimization, we introduce a differentiable formulation of the regularized AURC using the SoftRank technique. Empirical evaluations demonstrate that our AURC-based loss achieves competitive class-wise calibration performance across a range of datasets and model architectures.

Beyond Segmentation: Confidence-Aware and Debiased Estimation of Ratio-based Biomarkers

Ratio-based biomarkers -- such as the proportion of necrotic tissue within a tumor -- are widely used in clinical practice to support diagnosis, prognosis and treatment planning. These biomarkers are typically estimated from soft segmentation outputs by computing region-wise ratios. Despite the high-stakes nature of clinical decision making, existing methods provide only point estimates, offering no measure of uncertainty. In this work, we propose a unified \textit{confidence-aware} framework for estimating ratio-based biomarkers. We conduct a systematic analysis of error propagation in the segmentation-to-biomarker pipeline and identify model miscalibration as the dominant source of uncertainty. To mitigate this, we incorporate a lightweight, post-hoc calibration module that can be applied using internal hospital data without retraining. We leverage a tunable parameter $Q$ to control the confidence level of the derived bounds, allowing adaptation towards clinical practice. Extensive experiments show that our method produces statistically sound confidence intervals, with tunable confidence levels, enabling more trustworthy application of predictive biomarkers in clinical workflows.

DAVE: Diagnostic benchmark for Audio Visual Evaluation

Audio-visual understanding is a rapidly evolving field that seeks to integrate and interpret information from both auditory and visual modalities. Despite recent advances in multi-modal learning, existing benchmarks often suffer from strong visual bias -- where answers can be inferred from visual data alone -- and provide only aggregate scores that conflate multiple sources of error. This makes it difficult to determine whether models struggle with visual understanding, audio interpretation, or audio-visual alignment. In this work, we introduce DAVE (Diagnostic Audio Visual Evaluation), a novel benchmark dataset designed to systematically evaluate audio-visual models across controlled challenges. DAVE alleviates existing limitations by (i) ensuring both modalities are necessary to answer correctly and (ii) decoupling evaluation into atomic subcategories. Our detailed analysis of state-of-the-art models reveals specific failure modes and provides targeted insights for improvement. By offering this standardized diagnostic framework, we aim to facilitate more robust development of audio-visual models. The dataset is released: https://github.com/gorjanradevski/dave

A Novel Characterization of the Population Area Under the Risk Coverage Curve (AURC) and Rates of Finite Sample Estimators

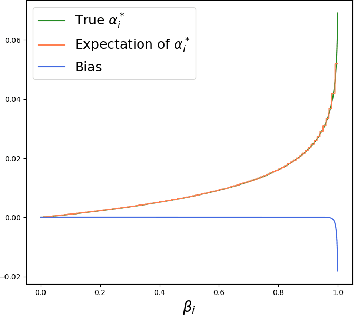
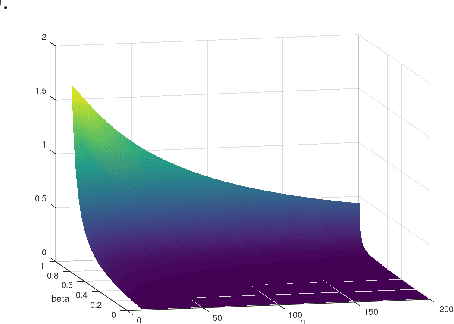
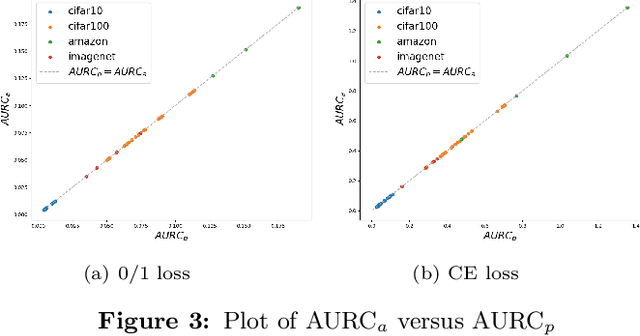
The selective classifier (SC) has garnered increasing interest in areas such as medical diagnostics, autonomous driving, and the justice system. The Area Under the Risk-Coverage Curve (AURC) has emerged as the foremost evaluation metric for assessing the performance of SC systems. In this work, we introduce a more straightforward representation of the population AURC, interpretable as a weighted risk function, and propose a Monte Carlo plug-in estimator applicable to finite sample scenarios. We demonstrate that our estimator is consistent and offers a low-bias estimation of the actual weights, with a tightly bounded mean squared error (MSE). We empirically show the effectiveness of this estimator on a comprehensive benchmark across multiple datasets, model architectures, and Confidence Score Functions (CSFs).

Estimating calibration error under label shift without labels

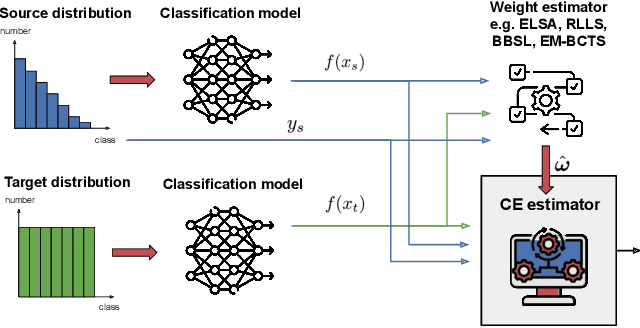
In the face of dataset shift, model calibration plays a pivotal role in ensuring the reliability of machine learning systems. Calibration error (CE) is an indicator of the alignment between the predicted probabilities and the classifier accuracy. While prior works have delved into the implications of dataset shift on calibration, existing CE estimators assume access to labels from the target domain, which are often unavailable in practice, i.e., when the model is deployed and used. This work addresses such challenging scenario, and proposes a novel CE estimator under label shift, which is characterized by changes in the marginal label distribution $p(Y)$, while keeping the conditional $p(X|Y)$ constant between the source and target distributions. Our contribution is an approach, which, by leveraging importance re-weighting of the labeled source distribution, provides consistent and asymptotically unbiased CE estimation with respect to the shifted target distribution. Empirical results across diverse real-world datasets, under various conditions and label-shift intensities, demonstrate the effectiveness and reliability of the proposed estimator.

Consistent and Asymptotically Unbiased Estimation of Proper Calibration Errors

Proper scoring rules evaluate the quality of probabilistic predictions, playing an essential role in the pursuit of accurate and well-calibrated models. Every proper score decomposes into two fundamental components -- proper calibration error and refinement -- utilizing a Bregman divergence. While uncertainty calibration has gained significant attention, current literature lacks a general estimator for these quantities with known statistical properties. To address this gap, we propose a method that allows consistent, and asymptotically unbiased estimation of all proper calibration errors and refinement terms. In particular, we introduce Kullback--Leibler calibration error, induced by the commonly used cross-entropy loss. As part of our results, we prove the relation between refinement and f-divergences, which implies information monotonicity in neural networks, regardless of which proper scoring rule is optimized. Our experiments validate empirically the claimed properties of the proposed estimator and suggest that the selection of a post-hoc calibration method should be determined by the particular calibration error of interest.

Beyond Classification: Definition and Density-based Estimation of Calibration in Object Detection

Despite their impressive predictive performance in various computer vision tasks, deep neural networks (DNNs) tend to make overly confident predictions, which hinders their widespread use in safety-critical applications. While there have been recent attempts to calibrate DNNs, most of these efforts have primarily been focused on classification tasks, thus neglecting DNN-based object detectors. Although several recent works addressed calibration for object detection and proposed differentiable penalties, none of them are consistent estimators of established concepts in calibration. In this work, we tackle the challenge of defining and estimating calibration error specifically for this task. In particular, we adapt the definition of classification calibration error to handle the nuances associated with object detection, and predictions in structured output spaces more generally. Furthermore, we propose a consistent and differentiable estimator of the detection calibration error, utilizing kernel density estimation. Our experiments demonstrate the effectiveness of our estimator against competing train-time and post-hoc calibration methods, while maintaining similar detection performance.

Dice Semimetric Losses: Optimizing the Dice Score with Soft Labels

The soft Dice loss (SDL) has taken a pivotal role in many automated segmentation pipelines in the medical imaging community. Over the last years, some reasons behind its superior functioning have been uncovered and further optimizations have been explored. However, there is currently no implementation that supports its direct use in settings with soft labels. Hence, a synergy between the use of SDL and research leveraging the use of soft labels, also in the context of model calibration, is still missing. In this work, we introduce Dice semimetric losses (DMLs), which (i) are by design identical to SDL in a standard setting with hard labels, but (ii) can be used in settings with soft labels. Our experiments on the public QUBIQ, LiTS and KiTS benchmarks confirm the potential synergy of DMLs with soft labels (e.g. averaging, label smoothing, and knowledge distillation) over hard labels (e.g. majority voting and random selection). As a result, we obtain superior Dice scores and model calibration, which supports the wider adoption of DMLs in practice. Code is available at \href{https://github.com/zifuwanggg/JDTLosses}{https://github.com/zifuwanggg/JDTLosses}.

A Consistent and Differentiable Lp Canonical Calibration Error Estimator

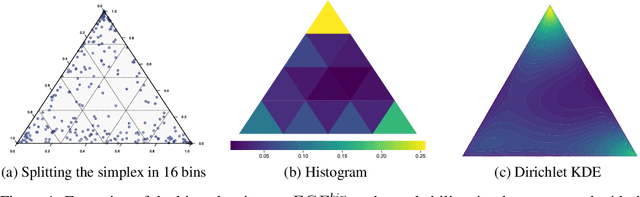
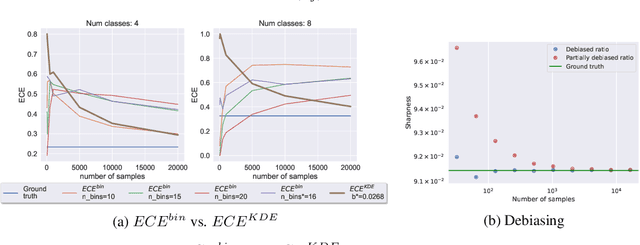
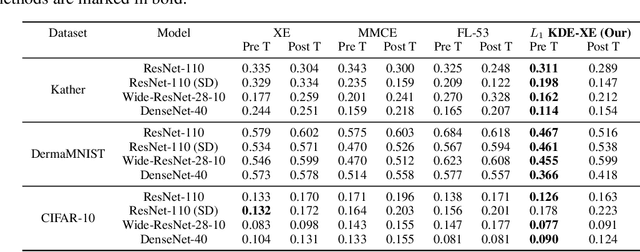
Calibrated probabilistic classifiers are models whose predicted probabilities can directly be interpreted as uncertainty estimates. It has been shown recently that deep neural networks are poorly calibrated and tend to output overconfident predictions. As a remedy, we propose a low-bias, trainable calibration error estimator based on Dirichlet kernel density estimates, which asymptotically converges to the true $L_p$ calibration error. This novel estimator enables us to tackle the strongest notion of multiclass calibration, called canonical (or distribution) calibration, while other common calibration methods are tractable only for top-label and marginal calibration. The computational complexity of our estimator is $\mathcal{O}(n^2)$, the convergence rate is $\mathcal{O}(n^{-1/2})$, and it is unbiased up to $\mathcal{O}(n^{-2})$, achieved by a geometric series debiasing scheme. In practice, this means that the estimator can be applied to small subsets of data, enabling efficient estimation and mini-batch updates. The proposed method has a natural choice of kernel, and can be used to generate consistent estimates of other quantities based on conditional expectation, such as the sharpness of a probabilistic classifier. Empirical results validate the correctness of our estimator, and demonstrate its utility in canonical calibration error estimation and calibration error regularized risk minimization.

On confidence intervals for precision matrices and the eigendecomposition of covariance matrices

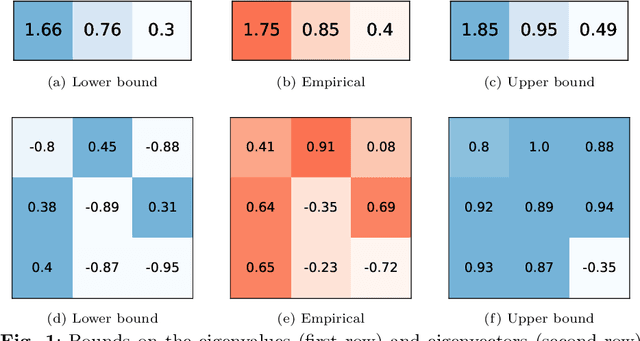
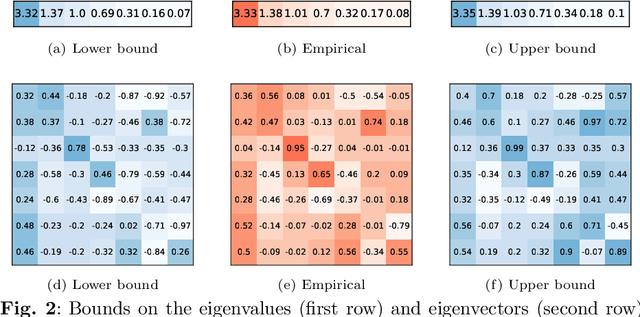
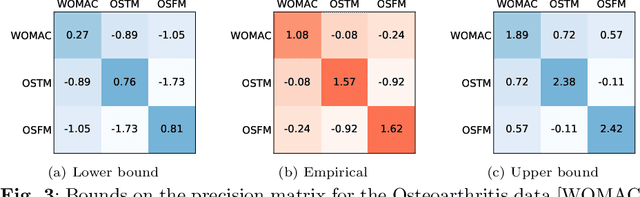
The eigendecomposition of a matrix is the central procedure in probabilistic models based on matrix factorization, for instance principal component analysis and topic models. Quantifying the uncertainty of such a decomposition based on a finite sample estimate is essential to reasoning under uncertainty when employing such models. This paper tackles the challenge of computing confidence bounds on the individual entries of eigenvectors of a covariance matrix of fixed dimension. Moreover, we derive a method to bound the entries of the inverse covariance matrix, the so-called precision matrix. The assumptions behind our method are minimal and require that the covariance matrix exists, and its empirical estimator converges to the true covariance. We make use of the theory of U-statistics to bound the $L_2$ perturbation of the empirical covariance matrix. From this result, we obtain bounds on the eigenvectors using Weyl's theorem and the eigenvalue-eigenvector identity and we derive confidence intervals on the entries of the precision matrix using matrix inversion perturbation bounds. As an application of these results, we demonstrate a new statistical test, which allows us to test for non-zero values of the precision matrix. We compare this test to the well-known Fisher-z test for partial correlations, and demonstrate the soundness and scalability of the proposed statistical test, as well as its application to real-world data from medical and physics domains.