A Novel Characterization of the Population Area Under the Risk Coverage Curve (AURC) and Rates of Finite Sample Estimators
Paper and Code
Oct 20, 2024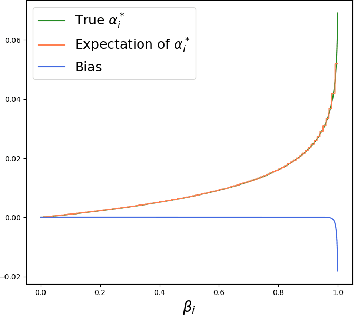
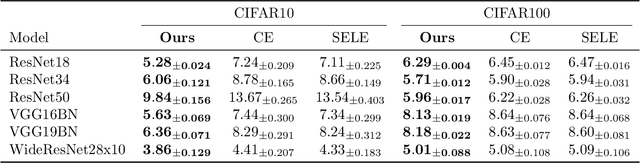
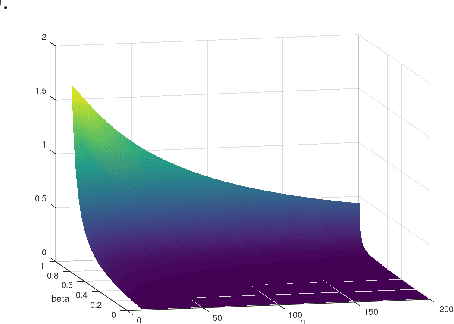
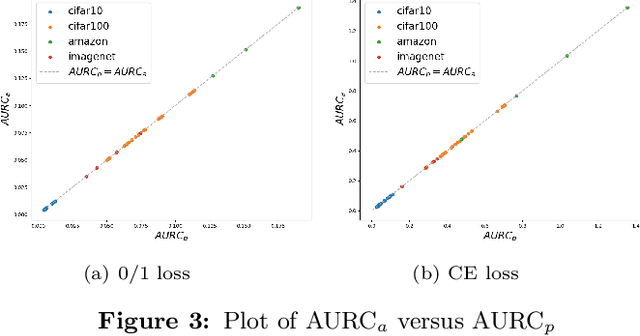
The selective classifier (SC) has garnered increasing interest in areas such as medical diagnostics, autonomous driving, and the justice system. The Area Under the Risk-Coverage Curve (AURC) has emerged as the foremost evaluation metric for assessing the performance of SC systems. In this work, we introduce a more straightforward representation of the population AURC, interpretable as a weighted risk function, and propose a Monte Carlo plug-in estimator applicable to finite sample scenarios. We demonstrate that our estimator is consistent and offers a low-bias estimation of the actual weights, with a tightly bounded mean squared error (MSE). We empirically show the effectiveness of this estimator on a comprehensive benchmark across multiple datasets, model architectures, and Confidence Score Functions (CSFs).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge