Hybrid Conditional Gradient - Smoothing Algorithms with Applications to Sparse and Low Rank Regularization

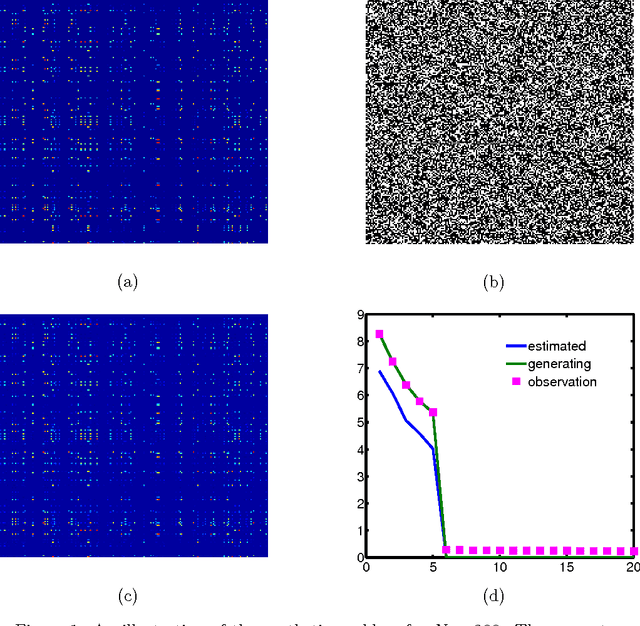
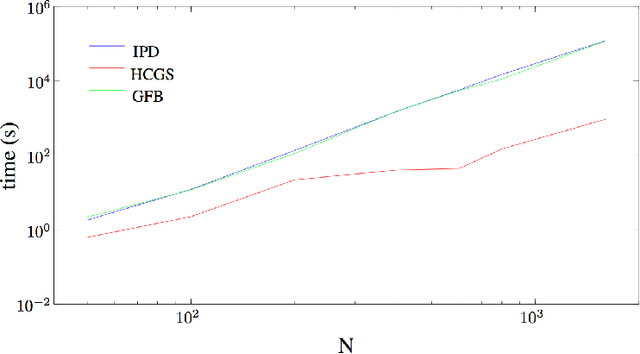
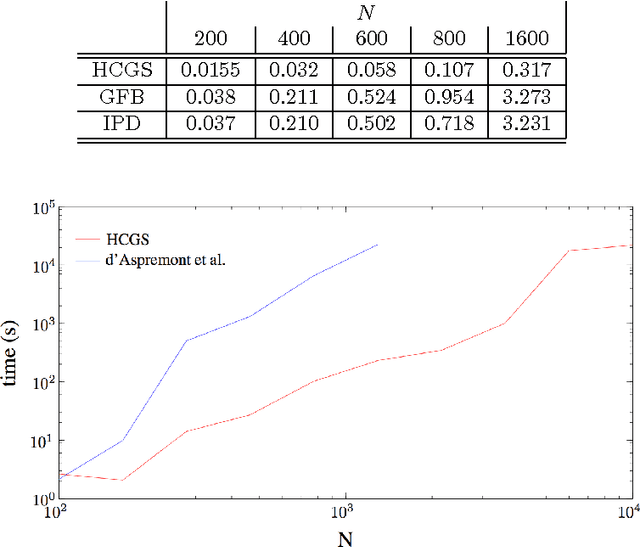
We study a hybrid conditional gradient - smoothing algorithm (HCGS) for solving composite convex optimization problems which contain several terms over a bounded set. Examples of these include regularization problems with several norms as penalties and a norm constraint. HCGS extends conditional gradient methods to cases with multiple nonsmooth terms, in which standard conditional gradient methods may be difficult to apply. The HCGS algorithm borrows techniques from smoothing proximal methods and requires first-order computations (subgradients and proximity operations). Unlike proximal methods, HCGS benefits from the advantages of conditional gradient methods, which render it more efficient on certain large scale optimization problems. We demonstrate these advantages with simulations on two matrix optimization problems: regularization of matrices with combined $\ell_1$ and trace norm penalties; and a convex relaxation of sparse PCA.

Learning Tensors in Reproducing Kernel Hilbert Spaces with Multilinear Spectral Penalties

We present a general framework to learn functions in tensor product reproducing kernel Hilbert spaces (TP-RKHSs). The methodology is based on a novel representer theorem suitable for existing as well as new spectral penalties for tensors. When the functions in the TP-RKHS are defined on the Cartesian product of finite discrete sets, in particular, our main problem formulation admits as a special case existing tensor completion problems. Other special cases include transfer learning with multimodal side information and multilinear multitask learning. For the latter case, our kernel-based view is instrumental to derive nonlinear extensions of existing model classes. We give a novel algorithm and show in experiments the usefulness of the proposed extensions.