Bayesian Optimization from Human Feedback: Near-Optimal Regret Bounds

Bayesian optimization (BO) with preference-based feedback has recently garnered significant attention due to its emerging applications. We refer to this problem as Bayesian Optimization from Human Feedback (BOHF), which differs from conventional BO by learning the best actions from a reduced feedback model, where only the preference between two actions is revealed to the learner at each time step. The objective is to identify the best action using a limited number of preference queries, typically obtained through costly human feedback. Existing work, which adopts the Bradley-Terry-Luce (BTL) feedback model, provides regret bounds for the performance of several algorithms. In this work, within the same framework we develop tighter performance guarantees. Specifically, we derive regret bounds of $\tilde{\mathcal{O}}(\sqrt{\Gamma(T)T})$, where $\Gamma(T)$ represents the maximum information gain$\unicode{x2014}$a kernel-specific complexity term$\unicode{x2014}$and $T$ is the number of queries. Our results significantly improve upon existing bounds. Notably, for common kernels, we show that the order-optimal sample complexities of conventional BO$\unicode{x2014}$achieved with richer feedback models$\unicode{x2014}$are recovered. In other words, the same number of preferential samples as scalar-valued samples is sufficient to find a nearly optimal solution.

Towards a Foundation Model for Communication Systems

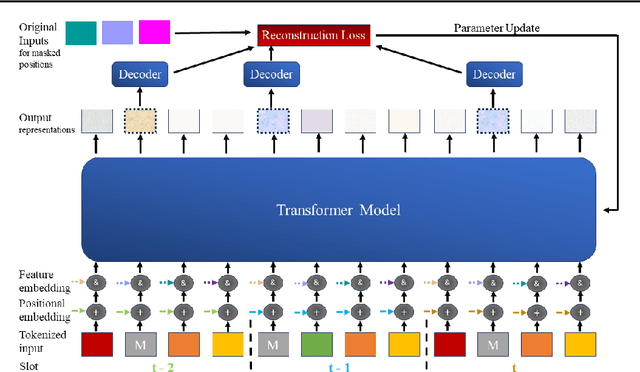
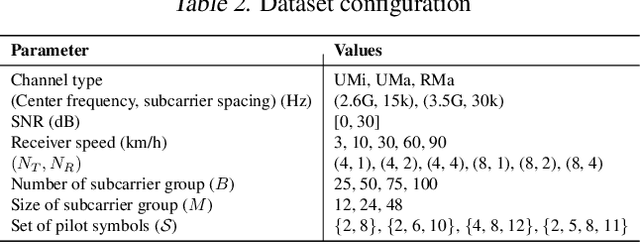
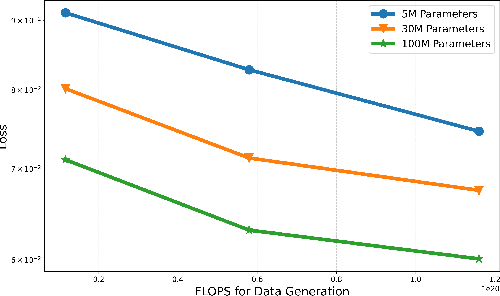
Artificial Intelligence (AI) has demonstrated unprecedented performance across various domains, and its application to communication systems is an active area of research. While current methods focus on task-specific solutions, the broader trend in AI is shifting toward large general models capable of supporting multiple applications. In this work, we take a step toward a foundation model for communication data--a transformer-based, multi-modal model designed to operate directly on communication data. We propose methodologies to address key challenges, including tokenization, positional embedding, multimodality, variable feature sizes, and normalization. Furthermore, we empirically demonstrate that such a model can successfully estimate multiple features, including transmission rank, selected precoder, Doppler spread, and delay profile.

Latent Flow Transformer

Transformers, the standard implementation for large language models (LLMs), typically consist of tens to hundreds of discrete layers. While more layers can lead to better performance, this approach has been challenged as far from efficient, especially given the superiority of continuous layers demonstrated by diffusion and flow-based models for image generation. We propose the Latent Flow Transformer (LFT), which replaces a block of layers with a single learned transport operator trained via flow matching, offering significant compression while maintaining compatibility with the original architecture. Additionally, we address the limitations of existing flow-based methods in \textit{preserving coupling} by introducing the Flow Walking (FW) algorithm. On the Pythia-410M model, LFT trained with flow matching compresses 6 of 24 layers and outperforms directly skipping 2 layers (KL Divergence of LM logits at 0.407 vs. 0.529), demonstrating the feasibility of this design. When trained with FW, LFT further distills 12 layers into one while reducing the KL to 0.736 surpassing that from skipping 3 layers (0.932), significantly narrowing the gap between autoregressive and flow-based generation paradigms.

Group Think: Multiple Concurrent Reasoning Agents Collaborating at Token Level Granularity

Recent advances in large language models (LLMs) have demonstrated the power of reasoning through self-generated chains of thought. Multiple reasoning agents can collaborate to raise joint reasoning quality above individual outcomes. However, such agents typically interact in a turn-based manner, trading increased latency for improved quality. In this paper, we propose Group Think--a single LLM that acts as multiple concurrent reasoning agents, or thinkers. With shared visibility into each other's partial generation progress, Group Think introduces a new concurrent-reasoning paradigm in which multiple reasoning trajectories adapt dynamically to one another at the token level. For example, a reasoning thread may shift its generation mid-sentence upon detecting that another thread is better positioned to continue. This fine-grained, token-level collaboration enables Group Think to reduce redundant reasoning and improve quality while achieving significantly lower latency. Moreover, its concurrent nature allows for efficient utilization of idle computational resources, making it especially suitable for edge inference, where very small batch size often underutilizes local~GPUs. We give a simple and generalizable modification that enables any existing LLM to perform Group Think on a local GPU. We also present an evaluation strategy to benchmark reasoning latency and empirically demonstrate latency improvements using open-source LLMs that were not explicitly trained for Group Think. We hope this work paves the way for future LLMs to exhibit more sophisticated and more efficient collaborative behavior for higher quality generation.

Enhancing Function-Calling Capabilities in LLMs: Strategies for Prompt Formats, Data Integration, and Multilingual Translation

Large language models (LLMs) have significantly advanced autonomous agents, particularly in zero-shot tool usage, also known as function calling. This research delves into enhancing the function-calling capabilities of LLMs by exploring different approaches, including prompt formats for integrating function descriptions, blending function-calling and instruction-following data, introducing a novel Decision Token for conditional prompts, leveraging chain-of-thought reasoning, and overcoming multilingual challenges with a translation pipeline. Our key findings and contributions are as follows: (1) Instruction-following data improves both function-calling accuracy and relevance detection. (2) The use of the newly proposed Decision Token, combined with synthetic non-function-call data, enhances relevance detection. (3) A tailored translation pipeline effectively overcomes multilingual limitations, demonstrating significant improvements in Traditional Chinese. These insights highlight the potential for improved function-calling capabilities and multilingual applications in LLMs.

Exact, Tractable Gauss-Newton Optimization in Deep Reversible Architectures Reveal Poor Generalization

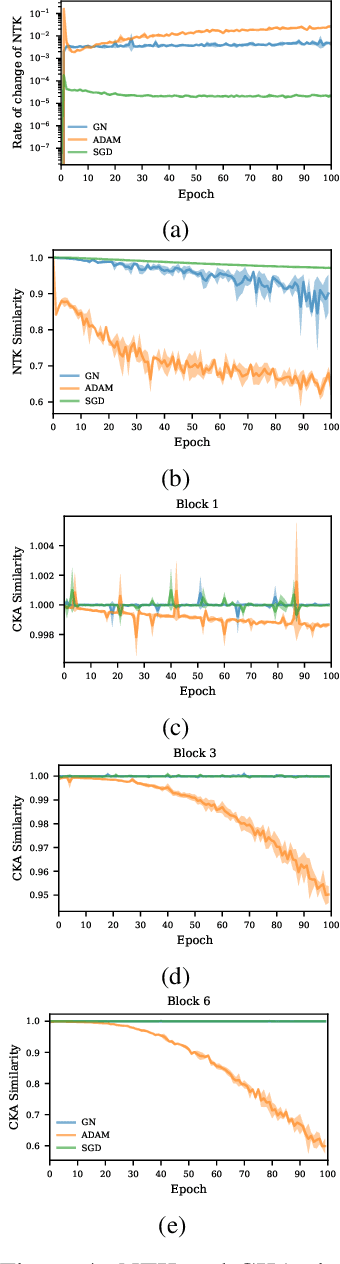
Second-order optimization has been shown to accelerate the training of deep neural networks in many applications, often yielding faster progress per iteration on the training loss compared to first-order optimizers. However, the generalization properties of second-order methods are still being debated. Theoretical investigations have proved difficult to carry out outside the tractable settings of heavily simplified model classes -- thus, the relevance of existing theories to practical deep learning applications remains unclear. Similarly, empirical studies in large-scale models and real datasets are significantly confounded by the necessity to approximate second-order updates in practice. It is often unclear whether the observed generalization behaviour arises specifically from the second-order nature of the parameter updates, or instead reflects the specific structured (e.g.\ Kronecker) approximations used or any damping-based interpolation towards first-order updates. Here, we show for the first time that exact Gauss-Newton (GN) updates take on a tractable form in a class of deep reversible architectures that are sufficiently expressive to be meaningfully applied to common benchmark datasets. We exploit this novel setting to study the training and generalization properties of the GN optimizer. We find that exact GN generalizes poorly. In the mini-batch training setting, this manifests as rapidly saturating progress even on the \emph{training} loss, with parameter updates found to overfit each mini-batchatch without producing the features that would support generalization to other mini-batches. We show that our experiments run in the ``lazy'' regime, in which the neural tangent kernel (NTK) changes very little during the course of training. This behaviour is associated with having no significant changes in neural representations, explaining the lack of generalization.

Let's Fuse Step by Step: A Generative Fusion Decoding Algorithm with LLMs for Multi-modal Text Recognition

We introduce ``Generative Fusion Decoding'' (GFD), a novel shallow fusion framework, utilized to integrate Large Language Models (LLMs) into multi-modal text recognition systems such as automatic speech recognition (ASR) and optical character recognition (OCR). We derive the formulas necessary to enable GFD to operate across mismatched token spaces of different models by mapping text token space to byte token space, enabling seamless fusion during the decoding process. The framework is plug-and-play, compatible with various auto-regressive models, and does not require re-training for feature alignment, thus overcoming limitations of previous fusion techniques. We highlight three main advantages of GFD: First, by simplifying the complexity of aligning different model sample spaces, GFD allows LLMs to correct errors in tandem with the recognition model, reducing computation latencies. Second, the in-context learning ability of LLMs is fully capitalized by GFD, increasing robustness in long-form speech recognition and instruction aware speech recognition. Third, GFD enables fusing recognition models deficient in Chinese text recognition with LLMs extensively trained on Chinese. Our evaluation demonstrates that GFD significantly improves performance in ASR and OCR tasks, with ASR reaching state-of-the-art in the NTUML2021 benchmark. GFD provides a significant step forward in model integration, offering a unified solution that could be widely applicable to leveraging existing pre-trained models through step by step fusion.

Advancing the Evaluation of Traditional Chinese Language Models: Towards a Comprehensive Benchmark Suite

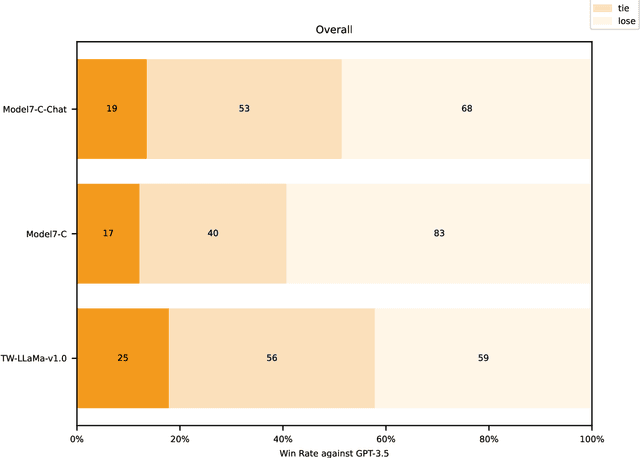
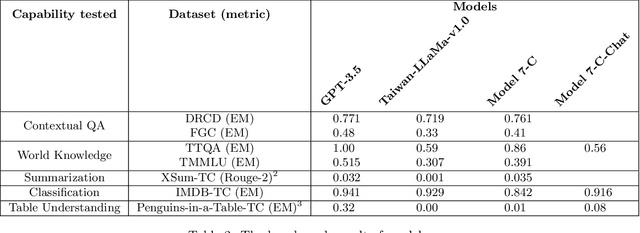
The evaluation of large language models is an essential task in the field of language understanding and generation. As language models continue to advance, the need for effective benchmarks to assess their performance has become imperative. In the context of Traditional Chinese, there is a scarcity of comprehensive and diverse benchmarks to evaluate the capabilities of language models, despite the existence of certain benchmarks such as DRCD, TTQA, CMDQA, and FGC dataset. To address this gap, we propose a novel set of benchmarks that leverage existing English datasets and are tailored to evaluate language models in Traditional Chinese. These benchmarks encompass a wide range of tasks, including contextual question-answering, summarization, classification, and table understanding. The proposed benchmarks offer a comprehensive evaluation framework, enabling the assessment of language models' capabilities across different tasks. In this paper, we evaluate the performance of GPT-3.5, Taiwan-LLaMa-v1.0, and Model 7-C, our proprietary model, on these benchmarks. The evaluation results highlight that our model, Model 7-C, achieves performance comparable to GPT-3.5 with respect to a part of the evaluated capabilities. In an effort to advance the evaluation of language models in Traditional Chinese and stimulate further research in this field, we have open-sourced our benchmark and opened the model for trial.

Generative Diffusion Models for Radio Wireless Channel Modelling and Sampling

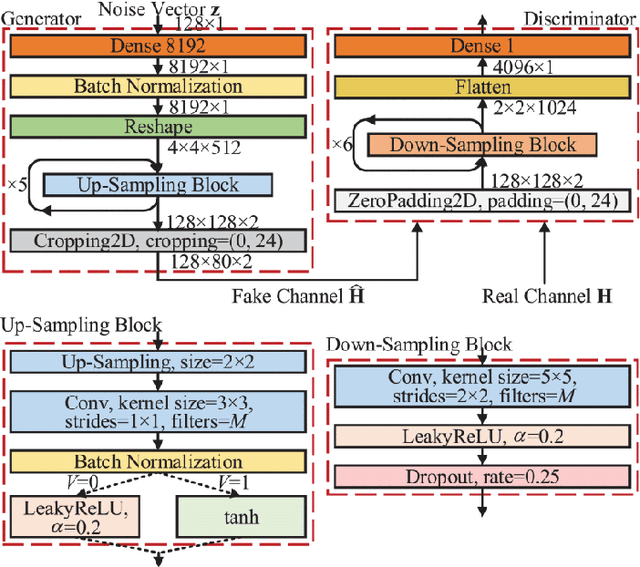
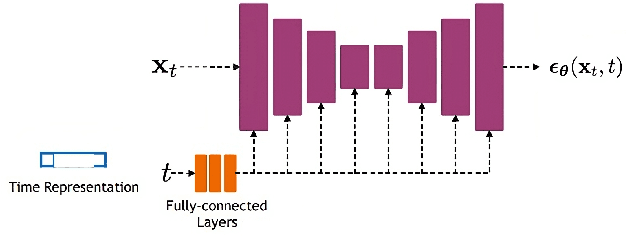
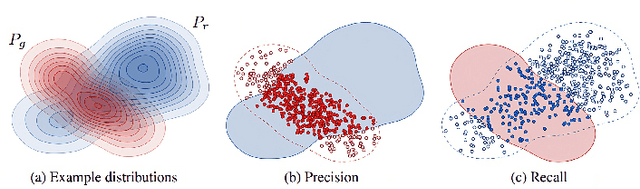
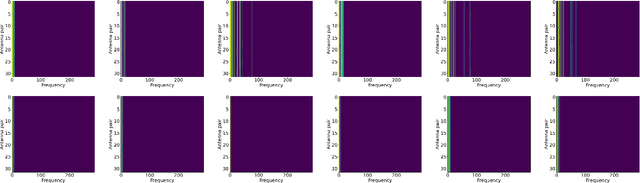
Channel modelling is essential to designing modern wireless communication systems. The increasing complexity of channel modelling and the cost of collecting high-quality wireless channel data have become major challenges. In this paper, we propose a diffusion model based channel sampling approach for rapidly synthesizing channel realizations from limited data. We use a diffusion model with a U Net based architecture operating in the frequency space domain. To evaluate how well the proposed model reproduces the true distribution of channels in the training dataset, two evaluation metrics are used: $i)$ the approximate $2$-Wasserstein distance between real and generated distributions of the normalized power spectrum in the antenna and frequency domains and $ii)$ precision and recall metric for distributions. We show that, compared to existing GAN based approaches which suffer from mode collapse and unstable training, our diffusion based approach trains stably and generates diverse and high-fidelity samples from the true channel distribution. We also show that we can pretrain the model on a simulated urban macro-cellular channel dataset and fine-tune it on a smaller, out-of-distribution urban micro-cellular dataset, therefore showing that it is feasible to model real world channels using limited data with this approach.

Zero-shot Domain-sensitive Speech Recognition with Prompt-conditioning Fine-tuning

In this work, we propose a method to create domain-sensitive speech recognition models that utilize textual domain information by conditioning its generation on a given text prompt. This is accomplished by fine-tuning a pre-trained, end-to-end model (Whisper) to learn from demonstrations with prompt examples. We show that this ability can be generalized to different domains and even various prompt contexts, with our model gaining a Word Error Rate (WER) reduction of up to 33% on unseen datasets from various domains, such as medical conversation, air traffic control communication, and financial meetings. Considering the limited availability of audio-transcript pair data, we further extend our method to text-only fine-tuning to achieve domain sensitivity as well as domain adaptation. We demonstrate that our text-only fine-tuned model can also attend to various prompt contexts, with the model reaching the most WER reduction of 29% on the medical conversation dataset.