A Collaborative, Human-Centred Taxonomy of AI, Algorithmic, and Automation Harms

This paper introduces a collaborative, human-centered taxonomy of AI, algorithmic and automation harms. We argue that existing taxonomies, while valuable, can be narrow, unclear, typically cater to practitioners and government, and often overlook the needs of the wider public. Drawing on existing taxonomies and a large repository of documented incidents, we propose a taxonomy that is clear and understandable to a broad set of audiences, as well as being flexible, extensible, and interoperable. Through iterative refinement with topic experts and crowdsourced annotation testing, we propose a taxonomy that can serve as a powerful tool for civil society organisations, educators, policymakers, product teams and the general public. By fostering a greater understanding of the real-world harms of AI and related technologies, we aim to increase understanding, empower NGOs and individuals to identify and report violations, inform policy discussions, and encourage responsible technology development and deployment.

Score Normalization for a Faster Diffusion Exponential Integrator Sampler

Recently, Zhang et al. have proposed the Diffusion Exponential Integrator Sampler (DEIS) for fast generation of samples from Diffusion Models. It leverages the semi-linear nature of the probability flow ordinary differential equation (ODE) in order to greatly reduce integration error and improve generation quality at low numbers of function evaluations (NFEs). Key to this approach is the score function reparameterisation, which reduces the integration error incurred from using a fixed score function estimate over each integration step. The original authors use the default parameterisation used by models trained for noise prediction -- multiply the score by the standard deviation of the conditional forward noising distribution. We find that although the mean absolute value of this score parameterisation is close to constant for a large portion of the reverse sampling process, it changes rapidly at the end of sampling. As a simple fix, we propose to instead reparameterise the score (at inference) by dividing it by the average absolute value of previous score estimates at that time step collected from offline high NFE generations. We find that our score normalisation (DEIS-SN) consistently improves FID compared to vanilla DEIS, showing an improvement at 10 NFEs from 6.44 to 5.57 on CIFAR-10 and from 5.9 to 4.95 on LSUN-Church 64x64. Our code is available at https://github.com/mtkresearch/Diffusion-DEIS-SN

Generative Diffusion Models for Radio Wireless Channel Modelling and Sampling

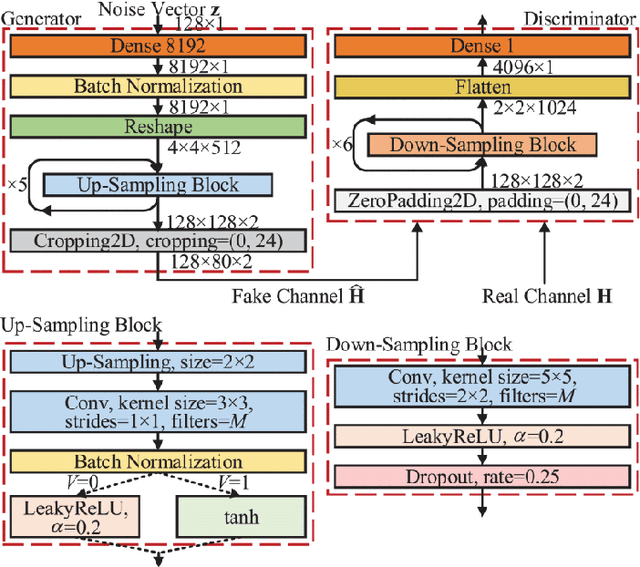
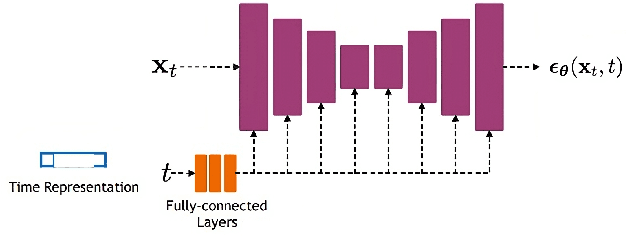
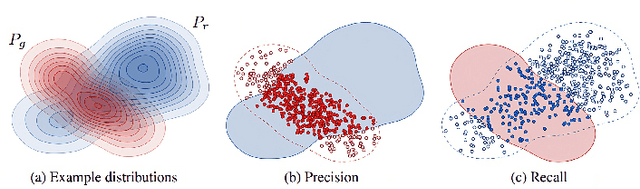
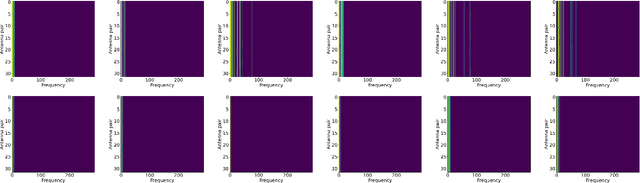
Channel modelling is essential to designing modern wireless communication systems. The increasing complexity of channel modelling and the cost of collecting high-quality wireless channel data have become major challenges. In this paper, we propose a diffusion model based channel sampling approach for rapidly synthesizing channel realizations from limited data. We use a diffusion model with a U Net based architecture operating in the frequency space domain. To evaluate how well the proposed model reproduces the true distribution of channels in the training dataset, two evaluation metrics are used: $i)$ the approximate $2$-Wasserstein distance between real and generated distributions of the normalized power spectrum in the antenna and frequency domains and $ii)$ precision and recall metric for distributions. We show that, compared to existing GAN based approaches which suffer from mode collapse and unstable training, our diffusion based approach trains stably and generates diverse and high-fidelity samples from the true channel distribution. We also show that we can pretrain the model on a simulated urban macro-cellular channel dataset and fine-tune it on a smaller, out-of-distribution urban micro-cellular dataset, therefore showing that it is feasible to model real world channels using limited data with this approach.

Forecasting Thermoacoustic Instabilities in Liquid Propellant Rocket Engines Using Multimodal Bayesian Deep Learning

The 100 MW cryogenic liquid oxygen/hydrogen multi-injector combustor BKD operated by the DLR Institute of Space Propulsion is a research platform that allows the study of thermoacoustic instabilities under realistic conditions, representative of small upper stage rocket engines. We use data from BKD experimental campaigns in which the static chamber pressure and fuel-oxidizer ratio are varied such that the first tangential mode of the combustor is excited under some conditions. We train an autoregressive Bayesian neural network model to forecast the amplitude of the dynamic pressure time series, inputting multiple sensor measurements (injector pressure/ temperature measurements, static chamber pressure, high-frequency dynamic pressure measurements, high-frequency OH* chemiluminescence measurements) and future flow rate control signals. The Bayesian nature of our algorithms allows us to work with a dataset whose size is restricted by the expense of each experimental run, without making overconfident extrapolations. We find that the networks are able to accurately forecast the evolution of the pressure amplitude and anticipate instability events on unseen experimental runs 500 milliseconds in advance. We compare the predictive accuracy of multiple models using different combinations of sensor inputs. We find that the high-frequency dynamic pressure signal is particularly informative. We also use the technique of integrated gradients to interpret the influence of different sensor inputs on the model prediction. The negative log-likelihood of data points in the test dataset indicates that predictive uncertainties are well-characterized by our Bayesian model and simulating a sensor failure event results as expected in a dramatic increase in the epistemic component of the uncertainty.

Simultaneous boundary shape estimation and velocity field de-noising in Magnetic Resonance Velocimetry using Physics-informed Neural Networks

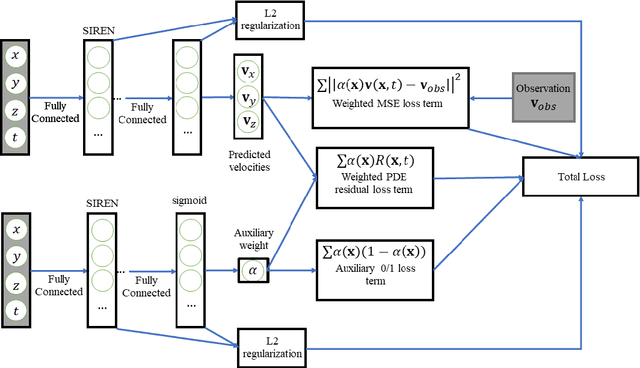
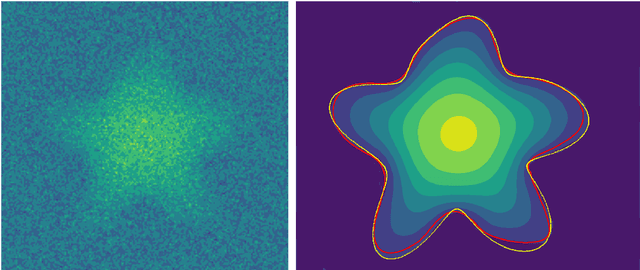
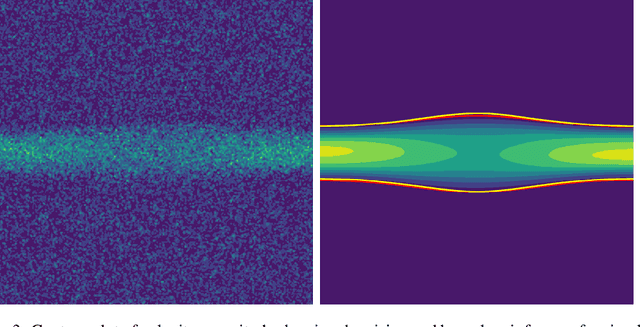
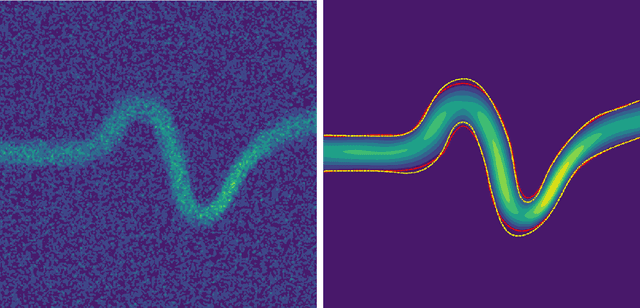
Magnetic resonance velocimetry (MRV) is a non-invasive experimental technique widely used in medicine and engineering to measure the velocity field of a fluid. These measurements are dense but have a low signal-to-noise ratio (SNR). The measurements can be de-noised by imposing physical constraints on the flow, which are encapsulated in governing equations for mass and momentum. Previous studies have required the shape of the boundary (for example, a blood vessel) to be known a priori. This, however, requires a set of additional measurements, which can be expensive to obtain. In this paper, we present a physics-informed neural network that instead uses the noisy MRV data alone to simultaneously infer the most likely boundary shape and de-noised velocity field. We achieve this by training an auxiliary neural network that takes the value 1.0 within the inferred domain of the governing PDE and 0.0 outside. This network is used to weight the PDE residual term in the loss function accordingly and implicitly learns the geometry of the system. We test our algorithm by assimilating both synthetic and real MRV measurements for flows that can be well modeled by the Poisson and Stokes equations. We find that we are able to reconstruct very noisy (SNR = 2.5) MRV signals and recover the ground truth with low reconstruction errors of 3.7 - 7.5%. The simplicity and flexibility of our physics-informed neural network approach can readily scale to assimilating MRV data with complex 3D geometries, time-varying 4D data, or unknown parameters in the physical model.

Online parameter inference for the simulation of a Bunsen flame using heteroscedastic Bayesian neural network ensembles

This paper proposes a Bayesian data-driven machine learning method for the online inference of the parameters of a G-equation model of a ducted, premixed flame. Heteroscedastic Bayesian neural network ensembles are trained on a library of 1.7 million flame fronts simulated in LSGEN2D, a G-equation solver, to learn the Bayesian posterior distribution of the model parameters given observations. The ensembles are then used to infer the parameters of Bunsen flame experiments so that the dynamics of these can be simulated in LSGEN2D. This allows the surface area variation of the flame edge, a proxy for the heat release rate, to be calculated. The proposed method provides cheap and online parameter and uncertainty estimates matching results obtained with the ensemble Kalman filter, at less computational cost. This enables fast and reliable simulation of the combustion process.

Early Detection of Thermoacoustic Instabilities in a Cryogenic Rocket Thrust Chamber using Combustion Noise Features and Machine Learning

Combustion instabilities are particularly problematic for rocket thrust chambers because of their high energy release rates and their operation close to the structural limits. In the last decades, progress has been made in predicting high amplitude combustion instabilities but still, no reliable prediction ability is given. Reliable early warning signals are the main requirement for active combustion control systems. In this paper, we present a data-driven method for the early detection of thermoacoustic instabilities. Recurrence quantification analysis is used to calculate characteristic combustion features from short-length time series of dynamic pressure sensor data. Features like the recurrence rate are used to train support vector machines to detect the onset of an instability a few hundred milliseconds in advance. The performance of the proposed method is investigated on experimental data from a representative LOX/H$_2$ research thrust chamber. In most cases, the method is able to timely predict two types of thermoacoustic instabilities on test data not used for training. The results are compared with state-of-the-art early warning indicators.

Ensembling geophysical models with Bayesian Neural Networks

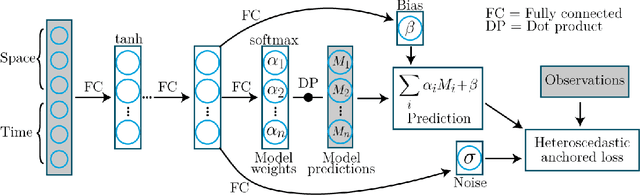
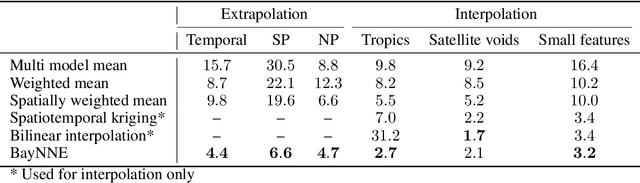
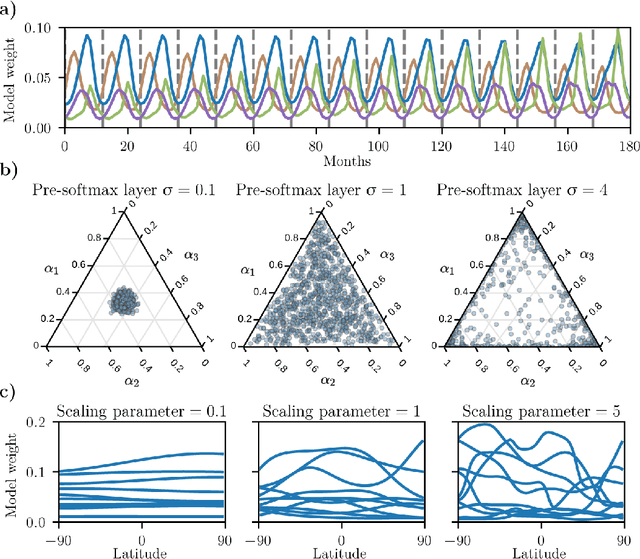
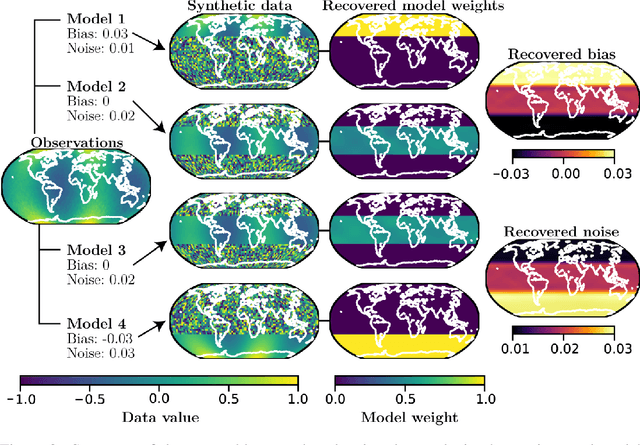
Ensembles of geophysical models improve projection accuracy and express uncertainties. We develop a novel data-driven ensembling strategy for combining geophysical models using Bayesian Neural Networks, which infers spatiotemporally varying model weights and bias while accounting for heteroscedastic uncertainties in the observations. This produces more accurate and uncertainty-aware projections without sacrificing interpretability. Applied to the prediction of total column ozone from an ensemble of 15 chemistry-climate models, we find that the Bayesian neural network ensemble (BayNNE) outperforms existing ensembling methods, achieving a 49.4% reduction in RMSE for temporal extrapolation, and a 67.4% reduction in RMSE for polar data voids, compared to a weighted mean. Uncertainty is also well-characterized, with 90.6% of the data points in our extrapolation validation dataset lying within 2 standard deviations and 98.5% within 3 standard deviations.