Simultaneous boundary shape estimation and velocity field de-noising in Magnetic Resonance Velocimetry using Physics-informed Neural Networks
Paper and Code
Jul 16, 2021
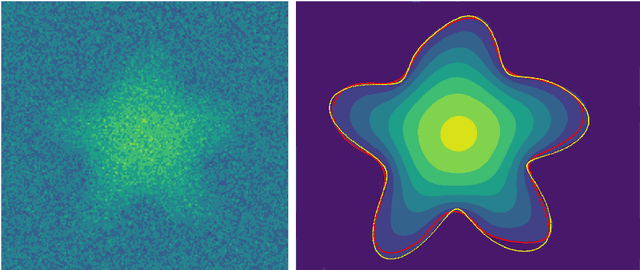
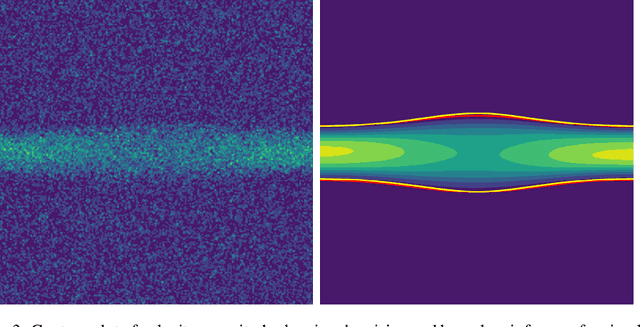
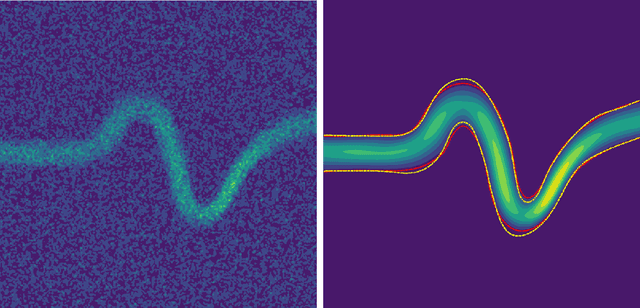
Magnetic resonance velocimetry (MRV) is a non-invasive experimental technique widely used in medicine and engineering to measure the velocity field of a fluid. These measurements are dense but have a low signal-to-noise ratio (SNR). The measurements can be de-noised by imposing physical constraints on the flow, which are encapsulated in governing equations for mass and momentum. Previous studies have required the shape of the boundary (for example, a blood vessel) to be known a priori. This, however, requires a set of additional measurements, which can be expensive to obtain. In this paper, we present a physics-informed neural network that instead uses the noisy MRV data alone to simultaneously infer the most likely boundary shape and de-noised velocity field. We achieve this by training an auxiliary neural network that takes the value 1.0 within the inferred domain of the governing PDE and 0.0 outside. This network is used to weight the PDE residual term in the loss function accordingly and implicitly learns the geometry of the system. We test our algorithm by assimilating both synthetic and real MRV measurements for flows that can be well modeled by the Poisson and Stokes equations. We find that we are able to reconstruct very noisy (SNR = 2.5) MRV signals and recover the ground truth with low reconstruction errors of 3.7 - 7.5%. The simplicity and flexibility of our physics-informed neural network approach can readily scale to assimilating MRV data with complex 3D geometries, time-varying 4D data, or unknown parameters in the physical model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge