Bayesian inverse Navier-Stokes problems: joint flow field reconstruction and parameter learning

We formulate and solve a Bayesian inverse Navier-Stokes (N-S) problem that assimilates velocimetry data in order to jointly reconstruct a 3D flow field and learn the unknown N-S parameters, including the boundary position. By hardwiring a generalised N-S problem, and regularising its unknown parameters using Gaussian prior distributions, we learn the most likely parameters in a collapsed search space. The most likely flow field reconstruction is then the N-S solution that corresponds to the learned parameters. We develop the method in the variational setting and use a stabilised Nitsche weak form of the N-S problem that permits the control of all N-S parameters. To regularise the inferred the geometry, we use a viscous signed distance field (vSDF) as an auxiliary variable, which is given as the solution of a viscous Eikonal boundary value problem. We devise an algorithm that solves this inverse problem, and numerically implement it using an adjoint-consistent stabilised cut-cell finite element method. We then use this method to reconstruct magnetic resonance velocimetry (flow-MRI) data of a 3D steady laminar flow through a physical model of an aortic arch for two different Reynolds numbers and signal-to-noise ratio (SNR) levels (low/high). We find that the method can accurately i) reconstruct the low SNR data by filtering out the noise/artefacts and recovering flow features that are obscured by noise, and ii) reproduce the high SNR data without overfitting. Although the framework that we develop applies to 3D steady laminar flows in complex geometries, it readily extends to time-dependent laminar and Reynolds-averaged turbulent flows, as well as non-Newtonian (e.g. viscoelastic) fluids.

Rapid Bayesian identification of sparse nonlinear dynamics from scarce and noisy data

We propose a fast probabilistic framework for identifying differential equations governing the dynamics of observed data. We recast the SINDy method within a Bayesian framework and use Gaussian approximations for the prior and likelihood to speed up computation. The resulting method, Bayesian-SINDy, not only quantifies uncertainty in the parameters estimated but also is more robust when learning the correct model from limited and noisy data. Using both synthetic and real-life examples such as Lynx-Hare population dynamics, we demonstrate the effectiveness of the new framework in learning correct model equations and compare its computational and data efficiency with existing methods. Because Bayesian-SINDy can quickly assimilate data and is robust against noise, it is particularly suitable for biological data and real-time system identification in control. Its probabilistic framework also enables the calculation of information entropy, laying the foundation for an active learning strategy.

Physics-informed compressed sensing for PC-MRI: an inverse Navier-Stokes problem

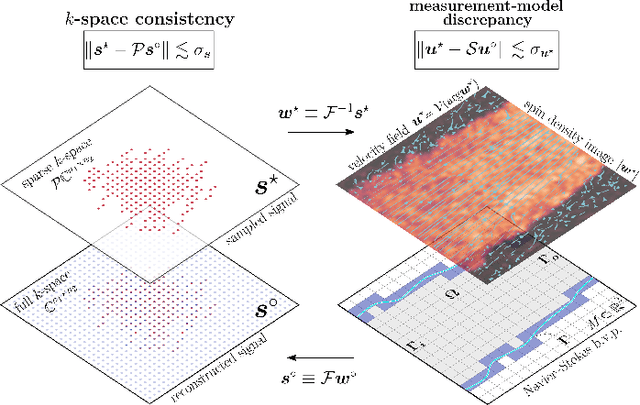
We formulate a physics-informed compressed sensing (PICS) method for the reconstruction of velocity fields from noisy and sparse phase-contrast magnetic resonance signals. The method solves an inverse Navier-Stokes boundary value problem, which permits us to jointly reconstruct and segment the velocity field, and at the same time infer hidden quantities such as the hydrodynamic pressure and the wall shear stress. Using a Bayesian framework, we regularize the problem by introducing a priori information about the unknown parameters in the form of Gaussian random fields. This prior information is updated using the Navier-Stokes problem, an energy-based segmentation functional, and by requiring that the reconstruction is consistent with the $k$-space signals. We create an algorithm that solves this reconstruction problem, and test it for noisy and sparse $k$-space signals of the flow through a converging nozzle. We find that the method is capable of reconstructing and segmenting the velocity fields from sparsely-sampled (15% $k$-space coverage), low ($\sim$$10$) signal-to-noise ratio (SNR) signals, and that the reconstructed velocity field compares well with that derived from fully-sampled (100% $k$-space coverage) high ($>40$) SNR signals of the same flow.

Forecasting Thermoacoustic Instabilities in Liquid Propellant Rocket Engines Using Multimodal Bayesian Deep Learning

The 100 MW cryogenic liquid oxygen/hydrogen multi-injector combustor BKD operated by the DLR Institute of Space Propulsion is a research platform that allows the study of thermoacoustic instabilities under realistic conditions, representative of small upper stage rocket engines. We use data from BKD experimental campaigns in which the static chamber pressure and fuel-oxidizer ratio are varied such that the first tangential mode of the combustor is excited under some conditions. We train an autoregressive Bayesian neural network model to forecast the amplitude of the dynamic pressure time series, inputting multiple sensor measurements (injector pressure/ temperature measurements, static chamber pressure, high-frequency dynamic pressure measurements, high-frequency OH* chemiluminescence measurements) and future flow rate control signals. The Bayesian nature of our algorithms allows us to work with a dataset whose size is restricted by the expense of each experimental run, without making overconfident extrapolations. We find that the networks are able to accurately forecast the evolution of the pressure amplitude and anticipate instability events on unseen experimental runs 500 milliseconds in advance. We compare the predictive accuracy of multiple models using different combinations of sensor inputs. We find that the high-frequency dynamic pressure signal is particularly informative. We also use the technique of integrated gradients to interpret the influence of different sensor inputs on the model prediction. The negative log-likelihood of data points in the test dataset indicates that predictive uncertainties are well-characterized by our Bayesian model and simulating a sensor failure event results as expected in a dramatic increase in the epistemic component of the uncertainty.

Simultaneous boundary shape estimation and velocity field de-noising in Magnetic Resonance Velocimetry using Physics-informed Neural Networks

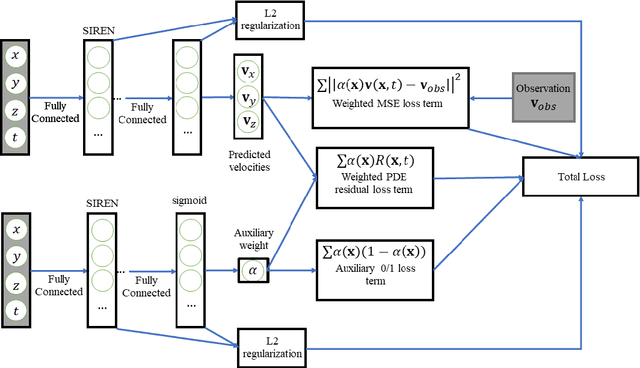
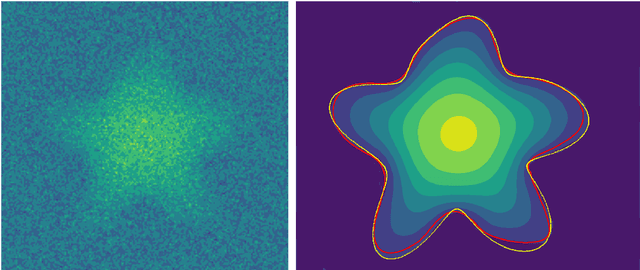
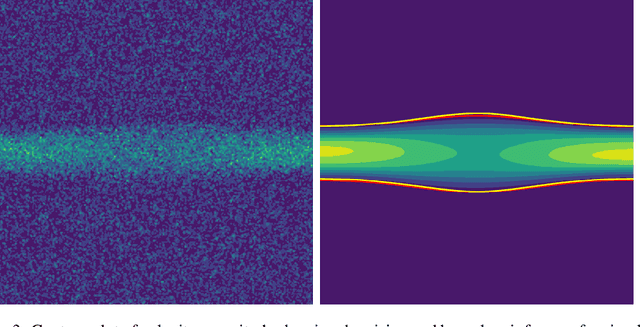
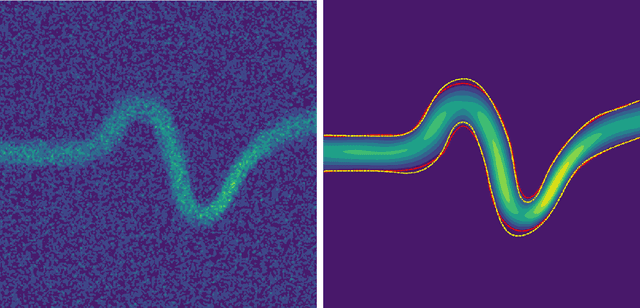
Magnetic resonance velocimetry (MRV) is a non-invasive experimental technique widely used in medicine and engineering to measure the velocity field of a fluid. These measurements are dense but have a low signal-to-noise ratio (SNR). The measurements can be de-noised by imposing physical constraints on the flow, which are encapsulated in governing equations for mass and momentum. Previous studies have required the shape of the boundary (for example, a blood vessel) to be known a priori. This, however, requires a set of additional measurements, which can be expensive to obtain. In this paper, we present a physics-informed neural network that instead uses the noisy MRV data alone to simultaneously infer the most likely boundary shape and de-noised velocity field. We achieve this by training an auxiliary neural network that takes the value 1.0 within the inferred domain of the governing PDE and 0.0 outside. This network is used to weight the PDE residual term in the loss function accordingly and implicitly learns the geometry of the system. We test our algorithm by assimilating both synthetic and real MRV measurements for flows that can be well modeled by the Poisson and Stokes equations. We find that we are able to reconstruct very noisy (SNR = 2.5) MRV signals and recover the ground truth with low reconstruction errors of 3.7 - 7.5%. The simplicity and flexibility of our physics-informed neural network approach can readily scale to assimilating MRV data with complex 3D geometries, time-varying 4D data, or unknown parameters in the physical model.

Online parameter inference for the simulation of a Bunsen flame using heteroscedastic Bayesian neural network ensembles

This paper proposes a Bayesian data-driven machine learning method for the online inference of the parameters of a G-equation model of a ducted, premixed flame. Heteroscedastic Bayesian neural network ensembles are trained on a library of 1.7 million flame fronts simulated in LSGEN2D, a G-equation solver, to learn the Bayesian posterior distribution of the model parameters given observations. The ensembles are then used to infer the parameters of Bunsen flame experiments so that the dynamics of these can be simulated in LSGEN2D. This allows the surface area variation of the flame edge, a proxy for the heat release rate, to be calculated. The proposed method provides cheap and online parameter and uncertainty estimates matching results obtained with the ensemble Kalman filter, at less computational cost. This enables fast and reliable simulation of the combustion process.

Combined State and Parameter Estimation in Level-Set Methods

Reduced-order models based on level-set methods are widely used tools to qualitatively capture and track the nonlinear dynamics of an interface. The aim of this paper is to develop a physics-informed, data-driven, statistically rigorous learning algorithm for state and parameter estimation with level-set methods. A Bayesian approach based on data assimilation is introduced. Data assimilation is enabled by the ensemble Kalman filter and smoother, which are used in their probabilistic formulations. The level-set data assimilation framework is verified in onedimensional and two-dimensional test cases, where state estimation, parameter estimation and uncertainty quantification are performed. The statistical performance of the proposed ensemble Kalman filter and smoother is quantified by twin experiments. In the twin experiments, the combined state and parameter estimation fully recovers the reference solution, which validates the proposed algorithm. The level-set data assimilation framework is then applied to the prediction of the nonlinear dynamics of a forced premixed flame, which exhibits the formation of sharp cusps and intricate topological changes, such as pinch-off events. The proposed physics-informed statistical learning algorithm opens up new possibilities for making reduced-order models of interfaces quantitatively predictive, any time that reference data is available.