Learning rheological parameters of non-Newtonian fluids from velocimetry data

We solve a Bayesian inverse Navier-Stokes (N-S) problem that assimilates velocimetry data in order to jointly reconstruct the flow field and learn the unknown N-S parameters. By incorporating a Carreau shear-thinning viscosity model into the N-S problem, we devise an algorithm that learns the most likely Carreau parameters of a shear-thinning fluid, and estimates their uncertainties, from velocimetry data alone. We then conduct a flow-MRI experiment to obtain velocimetry data of an axisymmetric laminar jet through an idealised medical device (FDA nozzle) for a blood analogue fluid. We show that the algorithm can successfully reconstruct the flow field by learning the most likely Carreau parameters, and that the learned parameters are in very good agreement with rheometry measurements. The algorithm accepts any algebraic effective viscosity model, as long as the model is differentiable, and it can be extended to more complicated non-Newtonian fluids (e.g. Oldroyd-B fluid) if a viscoelastic model is incorporated into the N-S problem.

Bayesian inverse Navier-Stokes problems: joint flow field reconstruction and parameter learning

We formulate and solve a Bayesian inverse Navier-Stokes (N-S) problem that assimilates velocimetry data in order to jointly reconstruct a 3D flow field and learn the unknown N-S parameters, including the boundary position. By hardwiring a generalised N-S problem, and regularising its unknown parameters using Gaussian prior distributions, we learn the most likely parameters in a collapsed search space. The most likely flow field reconstruction is then the N-S solution that corresponds to the learned parameters. We develop the method in the variational setting and use a stabilised Nitsche weak form of the N-S problem that permits the control of all N-S parameters. To regularise the inferred the geometry, we use a viscous signed distance field (vSDF) as an auxiliary variable, which is given as the solution of a viscous Eikonal boundary value problem. We devise an algorithm that solves this inverse problem, and numerically implement it using an adjoint-consistent stabilised cut-cell finite element method. We then use this method to reconstruct magnetic resonance velocimetry (flow-MRI) data of a 3D steady laminar flow through a physical model of an aortic arch for two different Reynolds numbers and signal-to-noise ratio (SNR) levels (low/high). We find that the method can accurately i) reconstruct the low SNR data by filtering out the noise/artefacts and recovering flow features that are obscured by noise, and ii) reproduce the high SNR data without overfitting. Although the framework that we develop applies to 3D steady laminar flows in complex geometries, it readily extends to time-dependent laminar and Reynolds-averaged turbulent flows, as well as non-Newtonian (e.g. viscoelastic) fluids.

Physics-informed compressed sensing for PC-MRI: an inverse Navier-Stokes problem

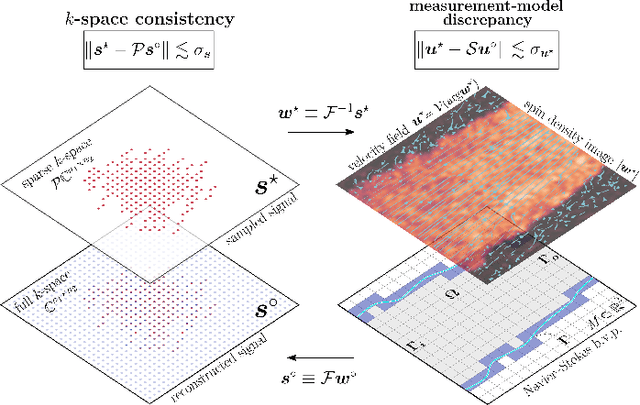
We formulate a physics-informed compressed sensing (PICS) method for the reconstruction of velocity fields from noisy and sparse phase-contrast magnetic resonance signals. The method solves an inverse Navier-Stokes boundary value problem, which permits us to jointly reconstruct and segment the velocity field, and at the same time infer hidden quantities such as the hydrodynamic pressure and the wall shear stress. Using a Bayesian framework, we regularize the problem by introducing a priori information about the unknown parameters in the form of Gaussian random fields. This prior information is updated using the Navier-Stokes problem, an energy-based segmentation functional, and by requiring that the reconstruction is consistent with the $k$-space signals. We create an algorithm that solves this reconstruction problem, and test it for noisy and sparse $k$-space signals of the flow through a converging nozzle. We find that the method is capable of reconstructing and segmenting the velocity fields from sparsely-sampled (15% $k$-space coverage), low ($\sim$$10$) signal-to-noise ratio (SNR) signals, and that the reconstructed velocity field compares well with that derived from fully-sampled (100% $k$-space coverage) high ($>40$) SNR signals of the same flow.

Simultaneous boundary shape estimation and velocity field de-noising in Magnetic Resonance Velocimetry using Physics-informed Neural Networks

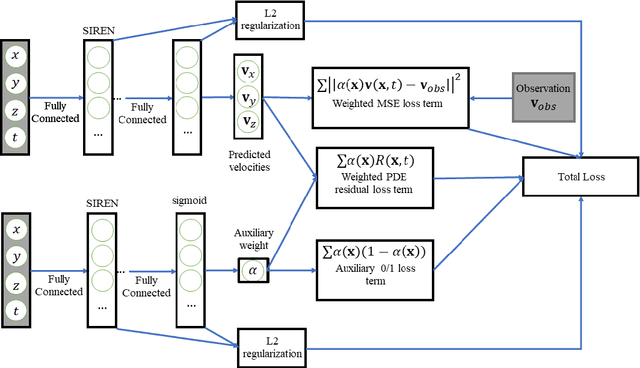
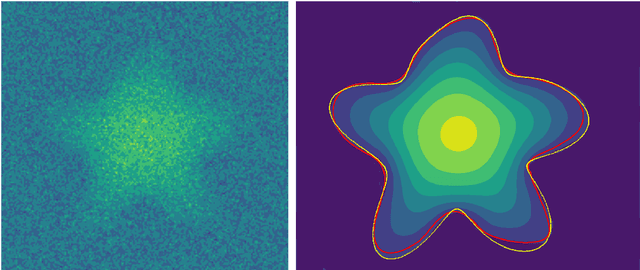
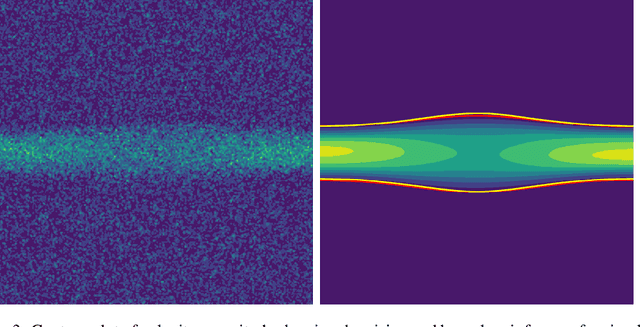
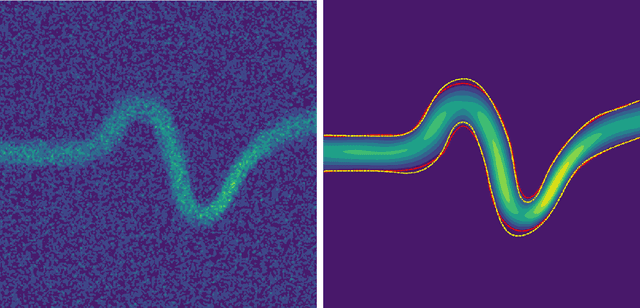
Magnetic resonance velocimetry (MRV) is a non-invasive experimental technique widely used in medicine and engineering to measure the velocity field of a fluid. These measurements are dense but have a low signal-to-noise ratio (SNR). The measurements can be de-noised by imposing physical constraints on the flow, which are encapsulated in governing equations for mass and momentum. Previous studies have required the shape of the boundary (for example, a blood vessel) to be known a priori. This, however, requires a set of additional measurements, which can be expensive to obtain. In this paper, we present a physics-informed neural network that instead uses the noisy MRV data alone to simultaneously infer the most likely boundary shape and de-noised velocity field. We achieve this by training an auxiliary neural network that takes the value 1.0 within the inferred domain of the governing PDE and 0.0 outside. This network is used to weight the PDE residual term in the loss function accordingly and implicitly learns the geometry of the system. We test our algorithm by assimilating both synthetic and real MRV measurements for flows that can be well modeled by the Poisson and Stokes equations. We find that we are able to reconstruct very noisy (SNR = 2.5) MRV signals and recover the ground truth with low reconstruction errors of 3.7 - 7.5%. The simplicity and flexibility of our physics-informed neural network approach can readily scale to assimilating MRV data with complex 3D geometries, time-varying 4D data, or unknown parameters in the physical model.