Preference Isolation Forest for Structure-based Anomaly Detection

We address the problem of detecting anomalies as samples that do not conform to structured patterns represented by low-dimensional manifolds. To this end, we conceive a general anomaly detection framework called Preference Isolation Forest (PIF), that combines the benefits of adaptive isolation-based methods with the flexibility of preference embedding. The key intuition is to embed the data into a high-dimensional preference space by fitting low-dimensional manifolds, and to identify anomalies as isolated points. We propose three isolation approaches to identify anomalies: $i$) Voronoi-iForest, the most general solution, $ii$) RuzHash-iForest, that avoids explicit computation of distances via Local Sensitive Hashing, and $iii$) Sliding-PIF, that leverages a locality prior to improve efficiency and effectiveness.

Hashing for Structure-based Anomaly Detection

We focus on the problem of identifying samples in a set that do not conform to structured patterns represented by low-dimensional manifolds. An effective way to solve this problem is to embed data in a high dimensional space, called Preference Space, where anomalies can be identified as the most isolated points. In this work, we employ Locality Sensitive Hashing to avoid explicit computation of distances in high dimensions and thus improve Anomaly Detection efficiency. Specifically, we present an isolation-based anomaly detection technique designed to work in the Preference Space which achieves state-of-the-art performance at a lower computational cost. Code is publicly available at https://github.com/ineveLoppiliF/Hashing-for-Structure-based-Anomaly-Detection.

MultiLink: Multi-class Structure Recovery via Agglomerative Clustering and Model Selection

We address the problem of recovering multiple structures of different classes in a dataset contaminated by noise and outliers. In particular, we consider geometric structures defined by a mixture of underlying parametric models (e.g. planes and cylinders, homographies and fundamental matrices), and we tackle the robust fitting problem by preference analysis and clustering. We present a new algorithm, termed MultiLink, that simultaneously deals with multiple classes of models. MultiLink combines on-the-fly model fitting and model selection in a novel linkage scheme that determines whether two clusters are to be merged. The resulting method features many practical advantages with respect to methods based on preference analysis, being faster, less sensitive to the inlier threshold, and able to compensate limitations deriving from hypotheses sampling. Experiments on several public datasets demonstrate that Multi-Link favourably compares with state of the art alternatives, both in multi-class and single-class problems. Code is publicly made available for download.

PIF: Anomaly detection via preference embedding

We address the problem of detecting anomalies with respect to structured patterns. To this end, we conceive a novel anomaly detection method called PIF, that combines the advantages of adaptive isolation methods with the flexibility of preference embedding. Specifically, we propose to embed the data in a high dimensional space where an efficient tree-based method, PI-Forest, is employed to compute an anomaly score. Experiments on synthetic and real datasets demonstrate that PIF favorably compares with state-of-the-art anomaly detection techniques, and confirm that PI-Forest is better at measuring arbitrary distances and isolate points in the preference space.

A Multimodal Hybrid Late-Cascade Fusion Network for Enhanced 3D Object Detection

We present a new way to detect 3D objects from multimodal inputs, leveraging both LiDAR and RGB cameras in a hybrid late-cascade scheme, that combines an RGB detection network and a 3D LiDAR detector. We exploit late fusion principles to reduce LiDAR False Positives, matching LiDAR detections with RGB ones by projecting the LiDAR bounding boxes on the image. We rely on cascade fusion principles to recover LiDAR False Negatives leveraging epipolar constraints and frustums generated by RGB detections of separate views. Our solution can be plugged on top of any underlying single-modal detectors, enabling a flexible training process that can take advantage of pre-trained LiDAR and RGB detectors, or train the two branches separately. We evaluate our results on the KITTI object detection benchmark, showing significant performance improvements, especially for the detection of Pedestrians and Cyclists.

Online model learning with data-assimilated reservoir computers

We propose an online learning framework for forecasting nonlinear spatio-temporal signals (fields). The method integrates (i) dimensionality reduction, here, a simple proper orthogonal decomposition (POD) projection; (ii) a generalized autoregressive model to forecast reduced dynamics, here, a reservoir computer; (iii) online adaptation to update the reservoir computer (the model), here, ensemble sequential data assimilation.We demonstrate the framework on a wake past a cylinder governed by the Navier-Stokes equations, exploring the assimilation of full flow fields (projected onto POD modes) and sparse sensors. Three scenarios are examined: a na\"ive physical state estimation; a two-fold estimation of physical and reservoir states; and a three-fold estimation that also adjusts the model parameters. The two-fold strategy significantly improves ensemble convergence and reduces reconstruction error compared to the na\"ive approach. The three-fold approach enables robust online training of partially-trained reservoir computers, overcoming limitations of a priori training. By unifying data-driven reduced order modelling with Bayesian data assimilation, this work opens new opportunities for scalable online model learning for nonlinear time series forecasting.

Data-Assimilated Model-Based Reinforcement Learning for Partially Observed Chaotic Flows

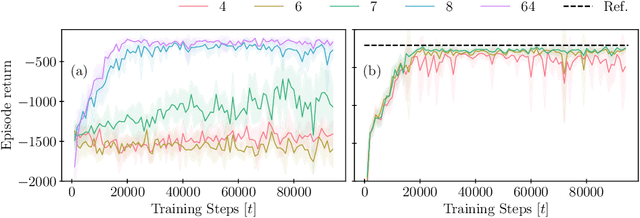
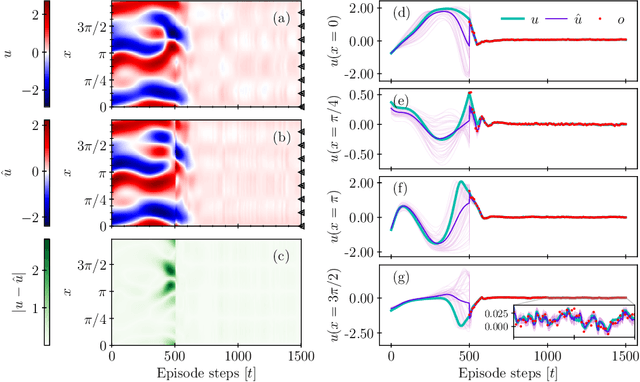
The goal of many applications in energy and transport sectors is to control turbulent flows. However, because of chaotic dynamics and high dimensionality, the control of turbulent flows is exceedingly difficult. Model-free reinforcement learning (RL) methods can discover optimal control policies by interacting with the environment, but they require full state information, which is often unavailable in experimental settings. We propose a data-assimilated model-based RL (DA-MBRL) framework for systems with partial observability and noisy measurements. Our framework employs a control-aware Echo State Network for data-driven prediction of the dynamics, and integrates data assimilation with an Ensemble Kalman Filter for real-time state estimation. An off-policy actor-critic algorithm is employed to learn optimal control strategies from state estimates. The framework is tested on the Kuramoto-Sivashinsky equation, demonstrating its effectiveness in stabilizing a spatiotemporally chaotic flow from noisy and partial measurements.

Outlier-Robust Multi-Model Fitting on Quantum Annealers

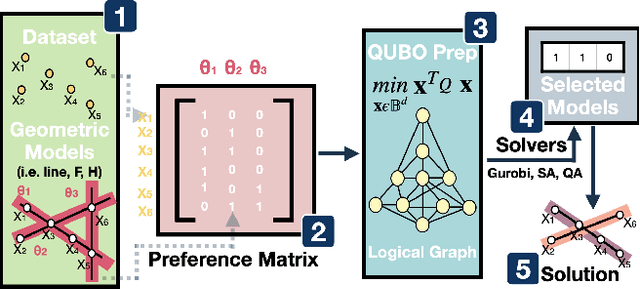
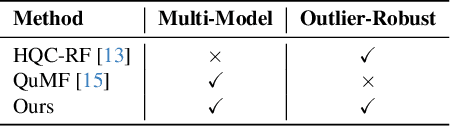
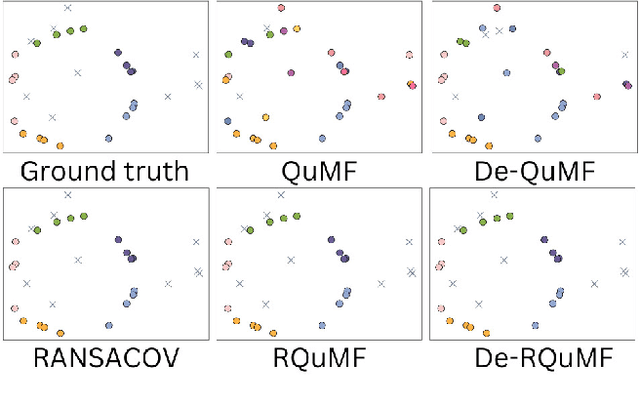
Multi-model fitting (MMF) presents a significant challenge in Computer Vision, particularly due to its combinatorial nature. While recent advancements in quantum computing offer promise for addressing NP-hard problems, existing quantum-based approaches for model fitting are either limited to a single model or consider multi-model scenarios within outlier-free datasets. This paper introduces a novel approach, the robust quantum multi-model fitting (R-QuMF) algorithm, designed to handle outliers effectively. Our method leverages the intrinsic capabilities of quantum hardware to tackle combinatorial challenges inherent in MMF tasks, and it does not require prior knowledge of the exact number of models, thereby enhancing its practical applicability. By formulating the problem as a maximum set coverage task for adiabatic quantum computers (AQC), R-QuMF outperforms existing quantum techniques, demonstrating superior performance across various synthetic and real-world 3D datasets. Our findings underscore the potential of quantum computing in addressing the complexities of MMF, especially in real-world scenarios with noisy and outlier-prone data.

Temporal-consistent CAMs for Weakly Supervised Video Segmentation in Waste Sorting

In industrial settings, weakly supervised (WS) methods are usually preferred over their fully supervised (FS) counterparts as they do not require costly manual annotations. Unfortunately, the segmentation masks obtained in the WS regime are typically poor in terms of accuracy. In this work, we present a WS method capable of producing accurate masks for semantic segmentation in the case of video streams. More specifically, we build saliency maps that exploit the temporal coherence between consecutive frames in a video, promoting consistency when objects appear in different frames. We apply our method in a waste-sorting scenario, where we perform weakly supervised video segmentation (WSVS) by training an auxiliary classifier that distinguishes between videos recorded before and after a human operator, who manually removes specific wastes from a conveyor belt. The saliency maps of this classifier identify materials to be removed, and we modify the classifier training to minimize differences between the saliency map of a central frame and those in adjacent frames, after having compensated object displacement. Experiments on a real-world dataset demonstrate the benefits of integrating temporal coherence directly during the training phase of the classifier. Code and dataset are available upon request.

Proper Latent Decomposition

In this paper, we introduce the proper latent decomposition (PLD) as a generalization of the proper orthogonal decomposition (POD) on manifolds. PLD is a nonlinear reduced-order modeling technique for compressing high-dimensional data into nonlinear coordinates. First, we compute a reduced set of intrinsic coordinates (latent space) to accurately describe a flow with fewer degrees of freedom than the numerical discretization. The latent space, which is geometrically a manifold, is inferred by an autoencoder. Second, we leverage tools from differential geometry to develop numerical methods for operating directly on the latent space; namely, a metric-constrained Eikonal solver for distance computations. With this proposed numerical framework, we propose an algorithm to perform PLD on the manifold. Third, we demonstrate results for a laminar flow case and the turbulent Kolmogorov flow. For the laminar flow case, we are able to identify a semi-analytical expression for the solution of Navier-Stokes; in the Kolmogorov flow case, we are able to identify a dominant mode that exhibits physical structures, which are compared with POD. This work opens opportunities for analyzing autoencoders and latent spaces, nonlinear reduced-order modeling and scientific insights into the structure of high-dimensional data.