Proper Latent Decomposition

In this paper, we introduce the proper latent decomposition (PLD) as a generalization of the proper orthogonal decomposition (POD) on manifolds. PLD is a nonlinear reduced-order modeling technique for compressing high-dimensional data into nonlinear coordinates. First, we compute a reduced set of intrinsic coordinates (latent space) to accurately describe a flow with fewer degrees of freedom than the numerical discretization. The latent space, which is geometrically a manifold, is inferred by an autoencoder. Second, we leverage tools from differential geometry to develop numerical methods for operating directly on the latent space; namely, a metric-constrained Eikonal solver for distance computations. With this proposed numerical framework, we propose an algorithm to perform PLD on the manifold. Third, we demonstrate results for a laminar flow case and the turbulent Kolmogorov flow. For the laminar flow case, we are able to identify a semi-analytical expression for the solution of Navier-Stokes; in the Kolmogorov flow case, we are able to identify a dominant mode that exhibits physical structures, which are compared with POD. This work opens opportunities for analyzing autoencoders and latent spaces, nonlinear reduced-order modeling and scientific insights into the structure of high-dimensional data.

Computing distances and means on manifolds with a metric-constrained Eikonal approach

Computing distances on Riemannian manifolds is a challenging problem with numerous applications, from physics, through statistics, to machine learning. In this paper, we introduce the metric-constrained Eikonal solver to obtain continuous, differentiable representations of distance functions on manifolds. The differentiable nature of these representations allows for the direct computation of globally length-minimising paths on the manifold. We showcase the use of metric-constrained Eikonal solvers for a range of manifolds and demonstrate the applications. First, we demonstrate that metric-constrained Eikonal solvers can be used to obtain the Fr\'echet mean on a manifold, employing the definition of a Gaussian mixture model, which has an analytical solution to verify the numerical results. Second, we demonstrate how the obtained distance function can be used to conduct unsupervised clustering on the manifold -- a task for which existing approaches are computationally prohibitive. This work opens opportunities for distance computations on manifolds.

Physics-constrained convolutional neural networks for inverse problems in spatiotemporal partial differential equations

We propose a physics-constrained convolutional neural network (PC-CNN) to solve two types of inverse problems in partial differential equations (PDEs), which are nonlinear and vary both in space and time. In the first inverse problem, we are given data that is offset by spatially varying systematic error (i.e., the bias, also known as the epistemic uncertainty). The task is to uncover from the biased data the true state, which is the solution of the PDE. In the second inverse problem, we are given sparse information on the solution of a PDE. The task is to reconstruct the solution in space with high-resolution. First, we present the PC-CNN, which constrains the PDE with a simple time-windowing scheme to handle sequential data. Second, we analyse the performance of the PC-CNN for uncovering solutions from biased data. We analyse both linear and nonlinear convection-diffusion equations, and the Navier-Stokes equations, which govern the spatiotemporally chaotic dynamics of turbulent flows. We find that the PC-CNN correctly recovers the true solution for a variety of biases, which are parameterised as non-convex functions. Third, we analyse the performance of the PC-CNN for reconstructing solutions from biased data for the turbulent flow. We reconstruct the spatiotemporal chaotic solution on a high-resolution grid from only 2\% of the information contained in it. For both tasks, we further analyse the Navier-Stokes solutions. We find that the inferred solutions have a physical spectral energy content, whereas traditional methods, such as interpolation, do not. This work opens opportunities for solving inverse problems with partial differential equations.

Manifold-augmented Eikonal Equations: Geodesic Distances and Flows on Differentiable Manifolds

Manifolds discovered by machine learning models provide a compact representation of the underlying data. Geodesics on these manifolds define locally length-minimising curves and provide a notion of distance, which are key for reduced-order modelling, statistical inference, and interpolation. In this work, we propose a model-based parameterisation for distance fields and geodesic flows on manifolds, exploiting solutions of a manifold-augmented Eikonal equation. We demonstrate how the geometry of the manifold impacts the distance field, and exploit the geodesic flow to obtain globally length-minimising curves directly. This work opens opportunities for statistics and reduced-order modelling on differentiable manifolds.

Super-resolving sparse observations in partial differential equations: A physics-constrained convolutional neural network approach

We propose the physics-constrained convolutional neural network (PC-CNN) to infer the high-resolution solution from sparse observations of spatiotemporal and nonlinear partial differential equations. Results are shown for a chaotic and turbulent fluid motion, whose solution is high-dimensional, and has fine spatiotemporal scales. We show that, by constraining prior physical knowledge in the CNN, we can infer the unresolved physical dynamics without using the high-resolution dataset in the training. This opens opportunities for super-resolution of experimental data and low-resolution simulations.

Uncovering solutions from data corrupted by systematic errors: A physics-constrained convolutional neural network approach

Information on natural phenomena and engineering systems is typically contained in data. Data can be corrupted by systematic errors in models and experiments. In this paper, we propose a tool to uncover the spatiotemporal solution of the underlying physical system by removing the systematic errors from data. The tool is the physics-constrained convolutional neural network (PC-CNN), which combines information from both the systems governing equations and data. We focus on fundamental phenomena that are modelled by partial differential equations, such as linear convection, Burgers equation, and two-dimensional turbulence. First, we formulate the problem, describe the physics-constrained convolutional neural network, and parameterise the systematic error. Second, we uncover the solutions from data corrupted by large multimodal systematic errors. Third, we perform a parametric study for different systematic errors. We show that the method is robust. Fourth, we analyse the physical properties of the uncovered solutions. We show that the solutions inferred from the PC-CNN are physical, in contrast to the data corrupted by systematic errors that does not fulfil the governing equations. This work opens opportunities for removing epistemic errors from models, and systematic errors from measurements.

Short and Straight: Geodesics on Differentiable Manifolds

Manifolds discovered by machine learning models provide a compact representation of the underlying data. Geodesics on these manifolds define locally length-minimising curves and provide a notion of distance, which are key for reduced-order modelling, statistical inference, and interpolation. In this work, we first analyse existing methods for computing length-minimising geodesics. We find that these are not suitable for obtaining valid paths, and thus, geodesic distances. We remedy these shortcomings by leveraging numerical tools from differential geometry, which provide the means to obtain Hamiltonian-conserving geodesics. Second, we propose a model-based parameterisation for distance fields and geodesic flows on continuous manifolds. Our approach exploits a manifold-aware extension to the Eikonal equation, eliminating the need for approximations or discretisation. Finally, we develop a curvature-based training mechanism, sampling and scaling points in regions of the manifold exhibiting larger values of the Ricci scalar. This sampling and scaling approach ensures that we capture regions of the manifold subject to higher degrees of geodesic deviation. Our proposed methods provide principled means to compute valid geodesics and geodesic distances on manifolds. This work opens opportunities for latent-space interpolation, optimal control, and distance computation on differentiable manifolds.

Physics-Informed CNNs for Super-Resolution of Sparse Observations on Dynamical Systems

In the absence of high-resolution samples, super-resolution of sparse observations on dynamical systems is a challenging problem with wide-reaching applications in experimental settings. We showcase the application of physics-informed convolutional neural networks for super-resolution of sparse observations on grids. Results are shown for the chaotic-turbulent Kolmogorov flow, demonstrating the potential of this method for resolving finer scales of turbulence when compared with classic interpolation methods, and thus effectively reconstructing missing physics.

Physics-Informed Convolutional Neural Networks for Corruption Removal on Dynamical Systems

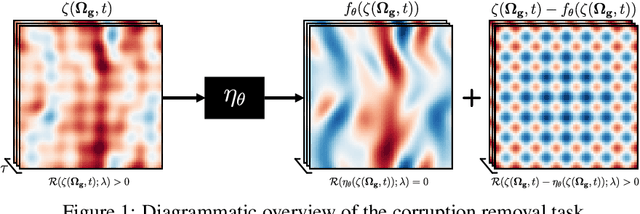
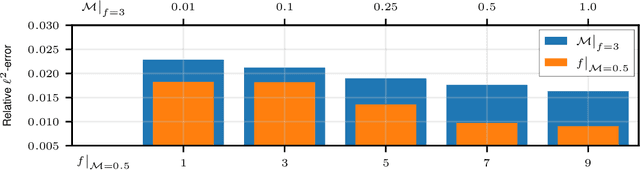
Measurements on dynamical systems, experimental or otherwise, are often subjected to inaccuracies capable of introducing corruption; removal of which is a problem of fundamental importance in the physical sciences. In this work we propose physics-informed convolutional neural networks for stationary corruption removal, providing the means to extract physical solutions from data, given access to partial ground-truth observations at collocation points. We showcase the methodology for 2D incompressible Navier-Stokes equations in the chaotic-turbulent flow regime, demonstrating robustness to modality and magnitude of corruption.