Unraveling Arithmetic in Large Language Models: The Role of Algebraic Structures

Large language models (LLMs) have demonstrated remarkable mathematical capabilities, largely driven by chain-of-thought (CoT) prompting, which decomposes complex reasoning into step-by-step solutions. This approach has enabled significant advancements, as evidenced by performance on benchmarks like GSM8K and MATH. However, the mechanisms underlying LLMs' ability to perform arithmetic in a single step of CoT remain poorly understood. Existing studies debate whether LLMs encode numerical values or rely on symbolic reasoning, while others explore attention and multi-layered processing in arithmetic tasks. In this work, we propose that LLMs learn arithmetic by capturing algebraic structures, such as \emph{Commutativity} and \emph{Identity} properties. Since these structures are observable through input-output relationships, they can generalize to unseen data. We empirically demonstrate that LLMs can learn algebraic structures using a custom dataset of arithmetic problems. Our findings indicate that leveraging algebraic structures can enhance the LLMs' arithmetic capabilities, offering insights into improving their arithmetic performance.

RL-STaR: Theoretical Analysis of Reinforcement Learning Frameworks for Self-Taught Reasoner

The reasoning abilities of large language models (LLMs) have improved with chain-of-thought (CoT) prompting, allowing models to solve complex tasks in a stepwise manner. However, training CoT capabilities requires detailed reasoning data, which is often scarce. The self-taught reasoner (STaR) framework addresses this by using reinforcement learning to automatically generate reasoning steps, reducing reliance on human-labeled data. Although STaR and its variants have demonstrated empirical success, a theoretical foundation explaining these improvements is lacking. This work provides a theoretical framework for understanding the effectiveness of reinforcement learning on CoT reasoning and STaR. Our contributions are: (1) an analysis of policy improvement, showing why LLM reasoning improves iteratively with STaR; (2) conditions for convergence to an optimal reasoning policy; (3) an examination of STaR's robustness, explaining how it can improve reasoning even when incorporating occasional incorrect steps; and (4) criteria for the quality of pre-trained models necessary to initiate effective reasoning improvement. This framework aims to bridge empirical findings with theoretical insights, advancing reinforcement learning approaches for reasoning in LLMs.

Leveraging Unlabeled Data Sharing through Kernel Function Approximation in Offline Reinforcement Learning

Offline reinforcement learning (RL) learns policies from a fixed dataset, but often requires large amounts of data. The challenge arises when labeled datasets are expensive, especially when rewards have to be provided by human labelers for large datasets. In contrast, unlabelled data tends to be less expensive. This situation highlights the importance of finding effective ways to use unlabelled data in offline RL, especially when labelled data is limited or expensive to obtain. In this paper, we present the algorithm to utilize the unlabeled data in the offline RL method with kernel function approximation and give the theoretical guarantee. We present various eigenvalue decay conditions of $\mathcal{H}_k$ which determine the complexity of the algorithm. In summary, our work provides a promising approach for exploiting the advantages offered by unlabeled data in offline RL, whilst maintaining theoretical assurances.

Sample Complexity of Kernel-Based Q-Learning

Modern reinforcement learning (RL) often faces an enormous state-action space. Existing analytical results are typically for settings with a small number of state-actions, or simple models such as linearly modeled Q-functions. To derive statistically efficient RL policies handling large state-action spaces, with more general Q-functions, some recent works have considered nonlinear function approximation using kernel ridge regression. In this work, we derive sample complexities for kernel based Q-learning when a generative model exists. We propose a nonparametric Q-learning algorithm which finds an $\epsilon$-optimal policy in an arbitrarily large scale discounted MDP. The sample complexity of the proposed algorithm is order optimal with respect to $\epsilon$ and the complexity of the kernel (in terms of its information gain). To the best of our knowledge, this is the first result showing a finite sample complexity under such a general model.

NTIRE 2020 Challenge on NonHomogeneous Dehazing

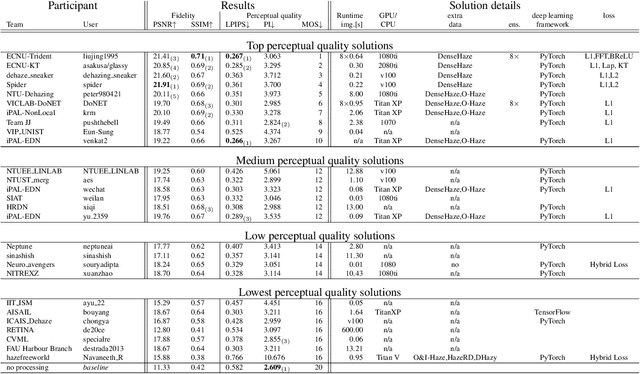
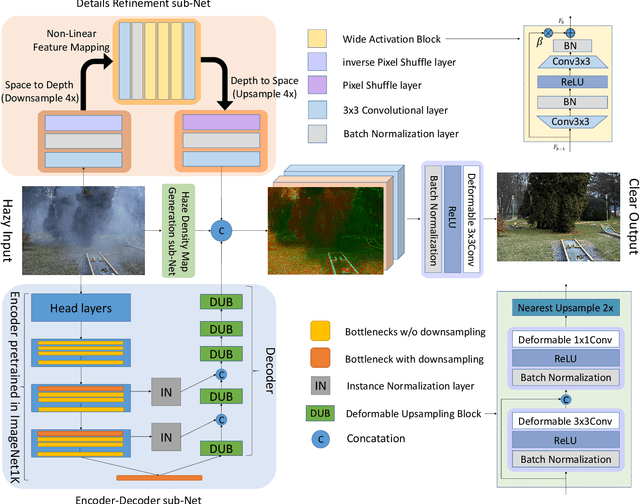
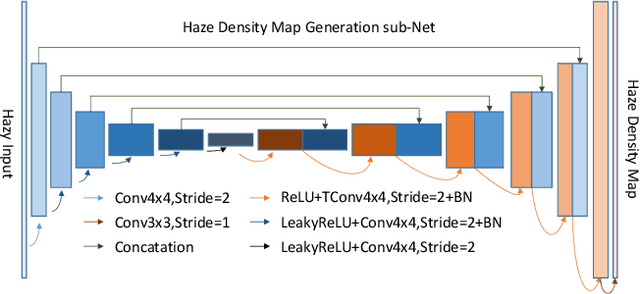
This paper reviews the NTIRE 2020 Challenge on NonHomogeneous Dehazing of images (restoration of rich details in hazy image). We focus on the proposed solutions and their results evaluated on NH-Haze, a novel dataset consisting of 55 pairs of real haze free and nonhomogeneous hazy images recorded outdoor. NH-Haze is the first realistic nonhomogeneous haze dataset that provides ground truth images. The nonhomogeneous haze has been produced using a professional haze generator that imitates the real conditions of haze scenes. 168 participants registered in the challenge and 27 teams competed in the final testing phase. The proposed solutions gauge the state-of-the-art in image dehazing.