Michael Bromberg
Uniform Generalization Bounds for Overparameterized Neural Networks
Sep 13, 2021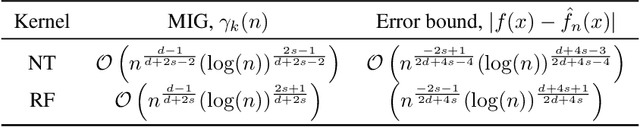

Abstract:An interesting observation in artificial neural networks is their favorable generalization error despite typically being extremely overparameterized. It is well known that classical statistical learning methods often result in vacuous generalization errors in the case of overparameterized neural networks. Adopting the recently developed Neural Tangent (NT) kernel theory, we prove uniform generalization bounds for overparameterized neural networks in kernel regimes, when the true data generating model belongs to the reproducing kernel Hilbert space (RKHS) corresponding to the NT kernel. Importantly, our bounds capture the exact error rates depending on the differentiability of the activation functions. In order to establish these bounds, we propose the information gain of the NT kernel as a measure of complexity of the learning problem. Our analysis uses a Mercer decomposition of the NT kernel in the basis of spherical harmonics and the decay rate of the corresponding eigenvalues. As a byproduct of our results, we show the equivalence between the RKHS corresponding to the NT kernel and its counterpart corresponding to the Mat\'ern family of kernels, that induces a very general class of models. We further discuss the implications of our analysis for some recent results on the regret bounds for reinforcement learning algorithms, which use overparameterized neural networks.
How to distribute data across tasks for meta-learning?
Mar 15, 2021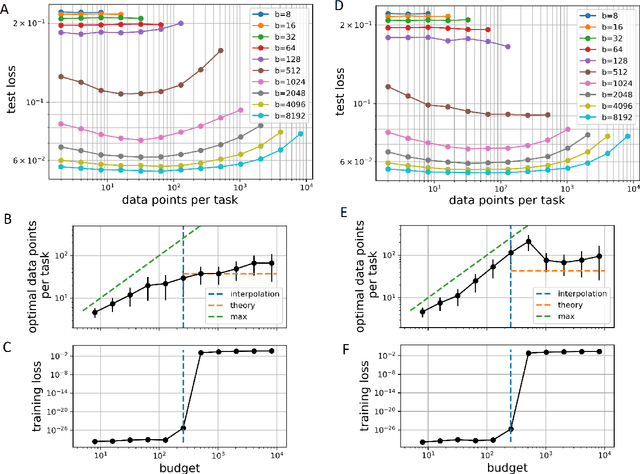
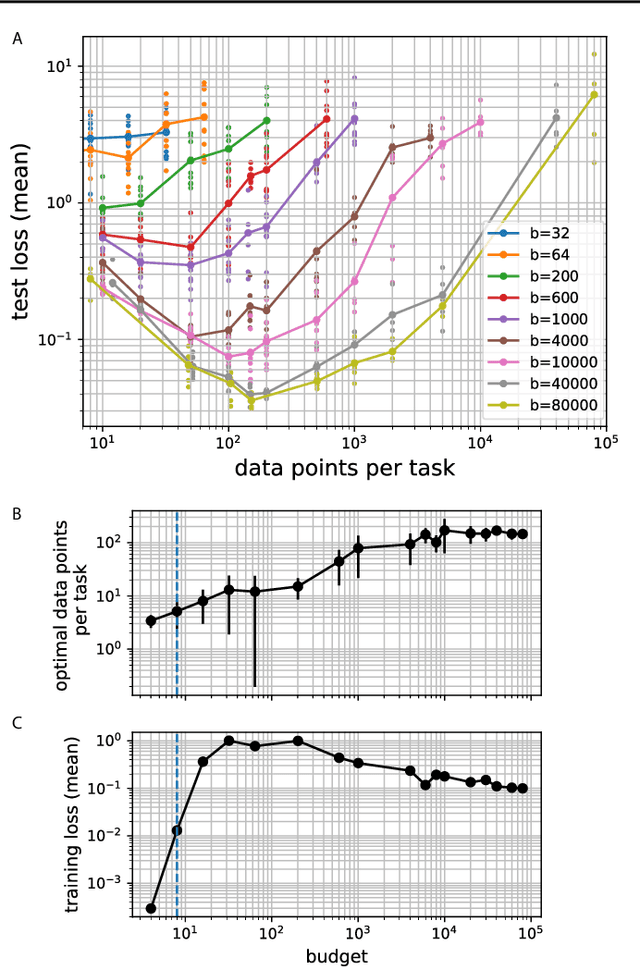
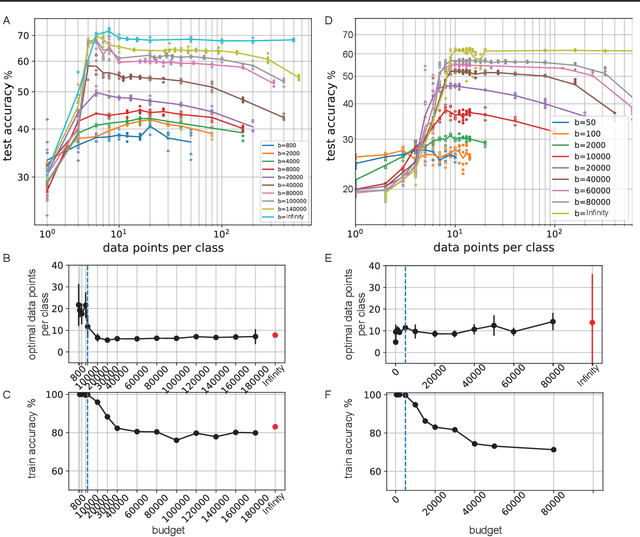
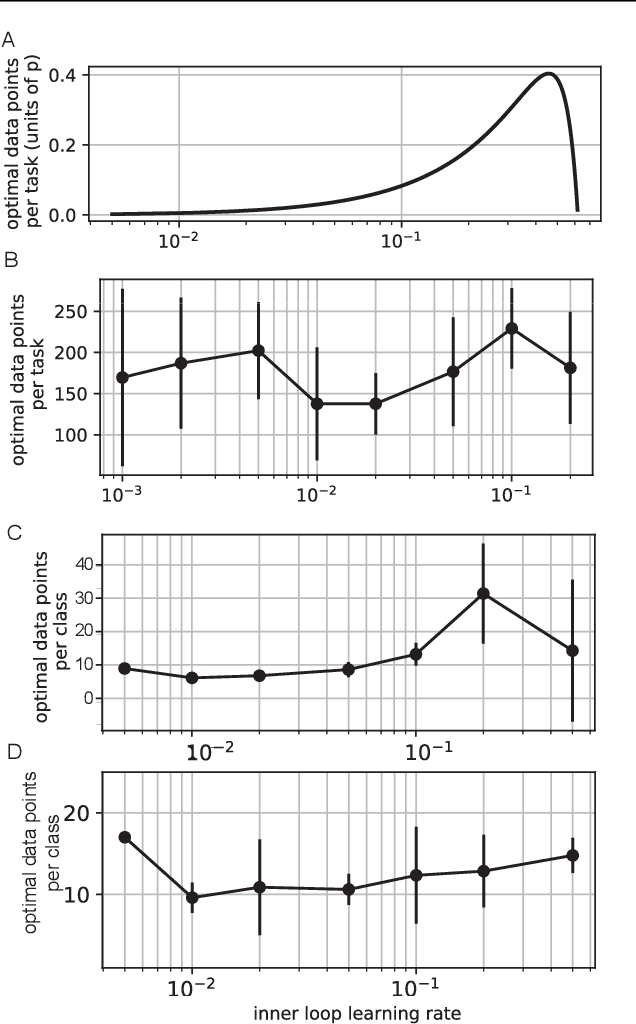
Abstract:Meta-learning models transfer the knowledge acquired from previous tasks to quickly learn new ones. They are tested on benchmarks with a fixed number of data points per training task. This number is usually arbitrary and it is unknown how it affects the performance. Since labelling of data is expensive, finding the optimal allocation of labels across training tasks may reduce costs: given a fixed budget of labels, should we use a small number of highly labelled tasks, or many tasks with few labels each? We show that: 1) The optimal number of data points per task depends on the budget, but it converges to a unique constant value for large budgets; 2) Convergence occurs around the interpolation threshold of the model. We prove our results mathematically on mixed linear regression, and we show empirically that the same results hold for nonlinear regression and few-shot image classification on CIFAR-FS and mini-ImageNet. Our results suggest a simple and efficient procedure for data collection: the optimal allocation of data can be computed at low cost, by using relatively small data, and collection of additional data can be optimized by the knowledge of the optimal allocation.
Cyclic orthogonal convolutions for long-range integration of features
Dec 11, 2020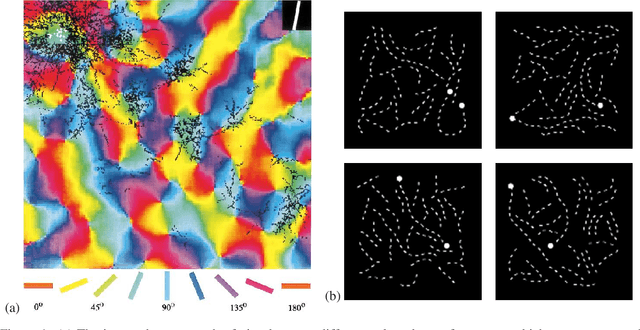

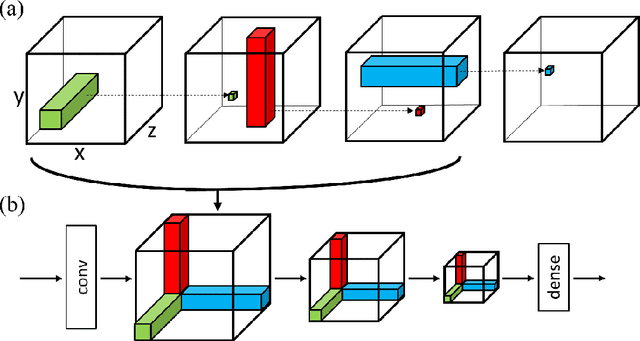
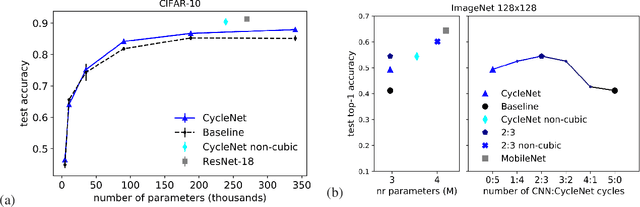
Abstract:In Convolutional Neural Networks (CNNs) information flows across a small neighbourhood of each pixel of an image, preventing long-range integration of features before reaching deep layers in the network. We propose a novel architecture that allows flexible information flow between features $z$ and locations $(x,y)$ across the entire image with a small number of layers. This architecture uses a cycle of three orthogonal convolutions, not only in $(x,y)$ coordinates, but also in $(x,z)$ and $(y,z)$ coordinates. We stack a sequence of such cycles to obtain our deep network, named CycleNet. As this only requires a permutation of the axes of a standard convolution, its performance can be directly compared to a CNN. Our model obtains competitive results at image classification on CIFAR-10 and ImageNet datasets, when compared to CNNs of similar size. We hypothesise that long-range integration favours recognition of objects by shape rather than texture, and we show that CycleNet transfers better than CNNs to stylised images. On the Pathfinder challenge, where integration of distant features is crucial, CycleNet outperforms CNNs by a large margin. We also show that even when employing a small convolutional kernel, the size of receptive fields of CycleNet reaches its maximum after one cycle, while conventional CNNs require a large number of layers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge