Cyclic orthogonal convolutions for long-range integration of features

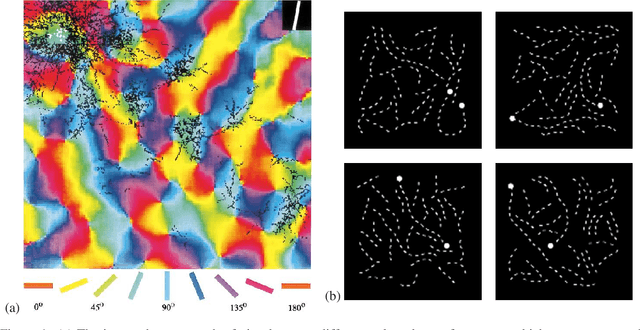
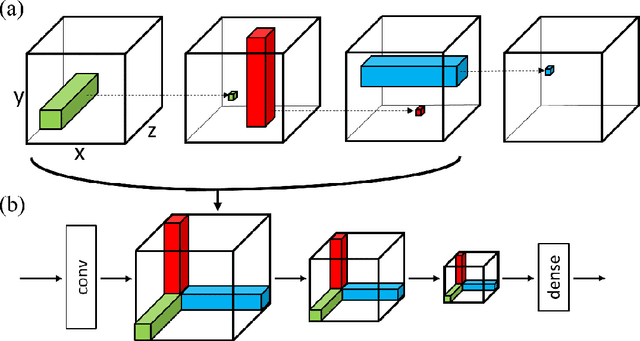
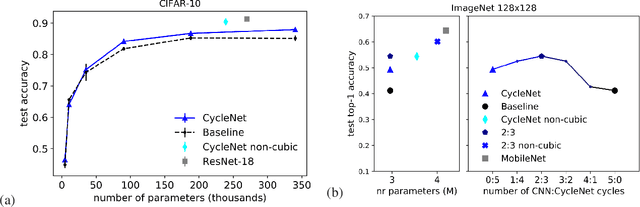
In Convolutional Neural Networks (CNNs) information flows across a small neighbourhood of each pixel of an image, preventing long-range integration of features before reaching deep layers in the network. We propose a novel architecture that allows flexible information flow between features $z$ and locations $(x,y)$ across the entire image with a small number of layers. This architecture uses a cycle of three orthogonal convolutions, not only in $(x,y)$ coordinates, but also in $(x,z)$ and $(y,z)$ coordinates. We stack a sequence of such cycles to obtain our deep network, named CycleNet. As this only requires a permutation of the axes of a standard convolution, its performance can be directly compared to a CNN. Our model obtains competitive results at image classification on CIFAR-10 and ImageNet datasets, when compared to CNNs of similar size. We hypothesise that long-range integration favours recognition of objects by shape rather than texture, and we show that CycleNet transfers better than CNNs to stylised images. On the Pathfinder challenge, where integration of distant features is crucial, CycleNet outperforms CNNs by a large margin. We also show that even when employing a small convolutional kernel, the size of receptive fields of CycleNet reaches its maximum after one cycle, while conventional CNNs require a large number of layers.

Compress and Control

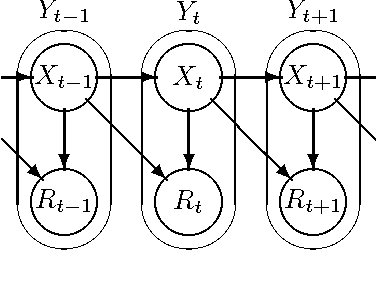
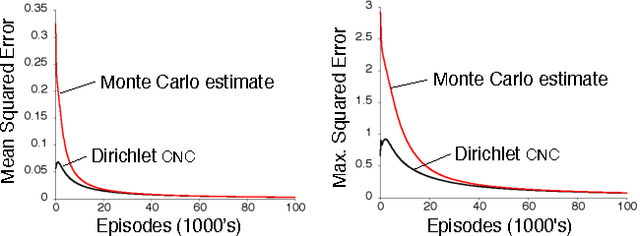
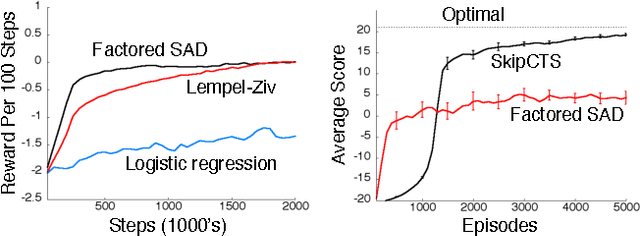
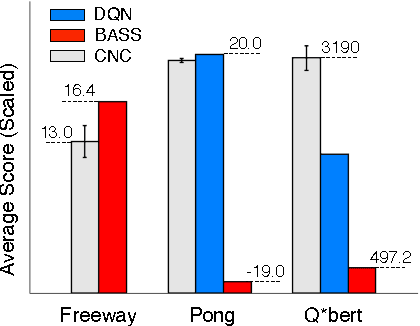
This paper describes a new information-theoretic policy evaluation technique for reinforcement learning. This technique converts any compression or density model into a corresponding estimate of value. Under appropriate stationarity and ergodicity conditions, we show that the use of a sufficiently powerful model gives rise to a consistent value function estimator. We also study the behavior of this technique when applied to various Atari 2600 video games, where the use of suboptimal modeling techniques is unavoidable. We consider three fundamentally different models, all too limited to perfectly model the dynamics of the system. Remarkably, we find that our technique provides sufficiently accurate value estimates for effective on-policy control. We conclude with a suggestive study highlighting the potential of our technique to scale to large problems.