Time Series Diffusion in the Frequency Domain

Fourier analysis has been an instrumental tool in the development of signal processing. This leads us to wonder whether this framework could similarly benefit generative modelling. In this paper, we explore this question through the scope of time series diffusion models. More specifically, we analyze whether representing time series in the frequency domain is a useful inductive bias for score-based diffusion models. By starting from the canonical SDE formulation of diffusion in the time domain, we show that a dual diffusion process occurs in the frequency domain with an important nuance: Brownian motions are replaced by what we call mirrored Brownian motions, characterized by mirror symmetries among their components. Building on this insight, we show how to adapt the denoising score matching approach to implement diffusion models in the frequency domain. This results in frequency diffusion models, which we compare to canonical time diffusion models. Our empirical evaluation on real-world datasets, covering various domains like healthcare and finance, shows that frequency diffusion models better capture the training distribution than time diffusion models. We explain this observation by showing that time series from these datasets tend to be more localized in the frequency domain than in the time domain, which makes them easier to model in the former case. All our observations point towards impactful synergies between Fourier analysis and diffusion models.

Closing the ODE-SDE gap in score-based diffusion models through the Fokker-Planck equation

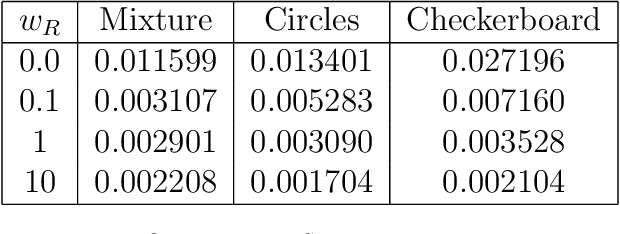
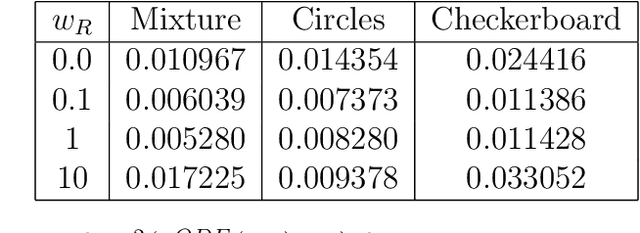
Score-based diffusion models have emerged as one of the most promising frameworks for deep generative modelling, due to their state-of-the art performance in many generation tasks while relying on mathematical foundations such as stochastic differential equations (SDEs) and ordinary differential equations (ODEs). Empirically, it has been reported that ODE based samples are inferior to SDE based samples. In this paper we rigorously describe the range of dynamics and approximations that arise when training score-based diffusion models, including the true SDE dynamics, the neural approximations, the various approximate particle dynamics that result, as well as their associated Fokker--Planck equations and the neural network approximations of these Fokker--Planck equations. We systematically analyse the difference between the ODE and SDE dynamics of score-based diffusion models, and link it to an associated Fokker--Planck equation. We derive a theoretical upper bound on the Wasserstein 2-distance between the ODE- and SDE-induced distributions in terms of a Fokker--Planck residual. We also show numerically that conventional score-based diffusion models can exhibit significant differences between ODE- and SDE-induced distributions which we demonstrate using explicit comparisons. Moreover, we show numerically that reducing the Fokker--Planck residual by adding it as an additional regularisation term leads to closing the gap between ODE- and SDE-induced distributions. Our experiments suggest that this regularisation can improve the distribution generated by the ODE, however that this can come at the cost of degraded SDE sample quality.

Variational Diffusion Auto-encoder: Deep Latent Variable Model with Unconditional Diffusion Prior

Variational auto-encoders (VAEs) are one of the most popular approaches to deep generative modeling. Despite their success, images generated by VAEs are known to suffer from blurriness, due to a highly unrealistic modeling assumption that the conditional data distribution $ p(\textbf{x} | \textbf{z})$ can be approximated as an isotropic Gaussian. In this work we introduce a principled approach to modeling the conditional data distribution $p(\textbf{x} | \textbf{z})$ by incorporating a diffusion model. We show that it is possible to create a VAE-like deep latent variable model without making the Gaussian assumption on $ p(\textbf{x} | \textbf{z}) $ or even training a decoder network. A trained encoder and an unconditional diffusion model can be combined via Bayes' rule for score functions to obtain an expressive model for $ p(\textbf{x} | \textbf{z}) $. Our approach avoids making strong assumptions on the parametric form of $ p(\textbf{x} | \textbf{z}) $, and thus allows to significantly improve the performance of VAEs.

Your diffusion model secretly knows the dimension of the data manifold

In this work, we propose a novel framework for estimating the dimension of the data manifold using a trained diffusion model. A trained diffusion model approximates the gradient of the log density of a noise-corrupted version of the target distribution for varying levels of corruption. If the data concentrates around a manifold embedded in the high-dimensional ambient space, then as the level of corruption decreases, the score function points towards the manifold, as this direction becomes the direction of maximum likelihood increase. Therefore, for small levels of corruption, the diffusion model provides us with access to an approximation of the normal bundle of the data manifold. This allows us to estimate the dimension of the tangent space, thus, the intrinsic dimension of the data manifold. Our method outperforms linear methods for dimensionality detection such as PPCA in controlled experiments.

Non-Uniform Diffusion Models

Diffusion models have emerged as one of the most promising frameworks for deep generative modeling. In this work, we explore the potential of non-uniform diffusion models. We show that non-uniform diffusion leads to multi-scale diffusion models which have similar structure to this of multi-scale normalizing flows. We experimentally find that in the same or less training time, the multi-scale diffusion model achieves better FID score than the standard uniform diffusion model. More importantly, it generates samples $4.4$ times faster in $128\times 128$ resolution. The speed-up is expected to be higher in higher resolutions where more scales are used. Moreover, we show that non-uniform diffusion leads to a novel estimator for the conditional score function which achieves on par performance with the state-of-the-art conditional denoising estimator. Our theoretical and experimental findings are accompanied by an open source library MSDiff which can facilitate further research of non-uniform diffusion models.

Classification of datasets with imputed missing values: does imputation quality matter?

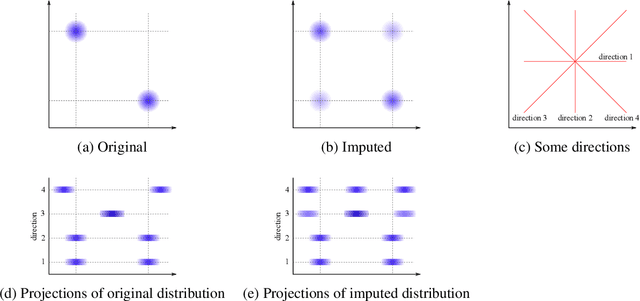
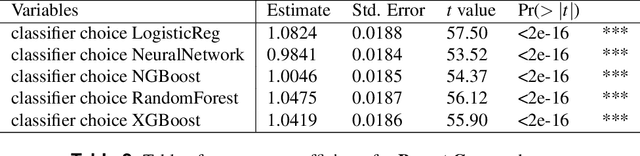
Classifying samples in incomplete datasets is a common aim for machine learning practitioners, but is non-trivial. Missing data is found in most real-world datasets and these missing values are typically imputed using established methods, followed by classification of the now complete, imputed, samples. The focus of the machine learning researcher is then to optimise the downstream classification performance. In this study, we highlight that it is imperative to consider the quality of the imputation. We demonstrate how the commonly used measures for assessing quality are flawed and propose a new class of discrepancy scores which focus on how well the method recreates the overall distribution of the data. To conclude, we highlight the compromised interpretability of classifier models trained using poorly imputed data.

Conditional Image Generation with Score-Based Diffusion Models

Score-based diffusion models have emerged as one of the most promising frameworks for deep generative modelling. In this work we conduct a systematic comparison and theoretical analysis of different approaches to learning conditional probability distributions with score-based diffusion models. In particular, we prove results which provide a theoretical justification for one of the most successful estimators of the conditional score. Moreover, we introduce a multi-speed diffusion framework, which leads to a new estimator for the conditional score, performing on par with previous state-of-the-art approaches. Our theoretical and experimental findings are accompanied by an open source library MSDiff which allows for application and further research of multi-speed diffusion models.

Wasserstein GANs Work Because They Fail (to Approximate the Wasserstein Distance)

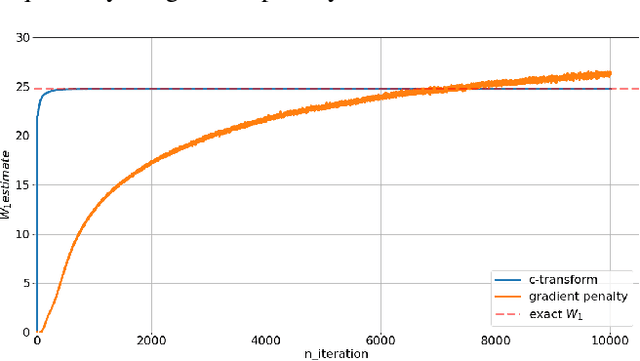
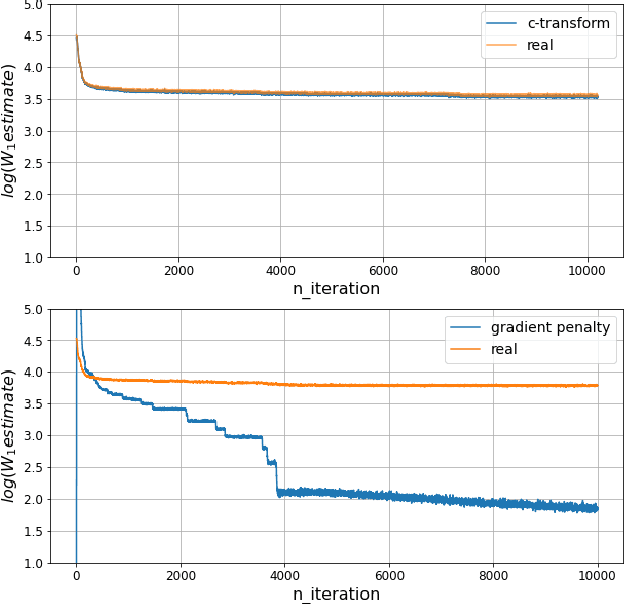
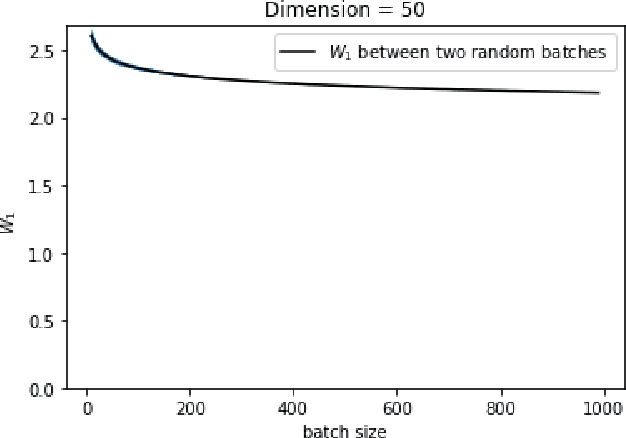
Wasserstein GANs are based on the idea of minimising the Wasserstein distance between a real and a generated distribution. We provide an in-depth mathematical analysis of differences between the theoretical setup and the reality of training Wasserstein GANs. In this work, we gather both theoretical and empirical evidence that the WGAN loss is not a meaningful approximation of the Wasserstein distance. Moreover, we argue that the Wasserstein distance is not even a desirable loss function for deep generative models, and conclude that the success of Wasserstein GANs can in truth be attributed to a failure to approximate the Wasserstein distance.