LaTable: Towards Large Tabular Models

Tabular data is one of the most ubiquitous modalities, yet the literature on tabular generative foundation models is lagging far behind its text and vision counterparts. Creating such a model is hard, due to the heterogeneous feature spaces of different tabular datasets, tabular metadata (e.g. dataset description and feature headers), and tables lacking prior knowledge (e.g. feature order). In this work we propose LaTable: a novel tabular diffusion model that addresses these challenges and can be trained across different datasets. Through extensive experiments we find that LaTable outperforms baselines on in-distribution generation, and that finetuning LaTable can generate out-of-distribution datasets better with fewer samples. On the other hand, we explore the poor zero-shot performance of LaTable, and what it may teach us about building generative tabular foundation models with better zero- and few-shot generation capabilities.

DAGnosis: Localized Identification of Data Inconsistencies using Structures

Identification and appropriate handling of inconsistencies in data at deployment time is crucial to reliably use machine learning models. While recent data-centric methods are able to identify such inconsistencies with respect to the training set, they suffer from two key limitations: (1) suboptimality in settings where features exhibit statistical independencies, due to their usage of compressive representations and (2) lack of localization to pin-point why a sample might be flagged as inconsistent, which is important to guide future data collection. We solve these two fundamental limitations using directed acyclic graphs (DAGs) to encode the training set's features probability distribution and independencies as a structure. Our method, called DAGnosis, leverages these structural interactions to bring valuable and insightful data-centric conclusions. DAGnosis unlocks the localization of the causes of inconsistencies on a DAG, an aspect overlooked by previous approaches. Moreover, we show empirically that leveraging these interactions (1) leads to more accurate conclusions in detecting inconsistencies, as well as (2) provides more detailed insights into why some samples are flagged.

Time Series Diffusion in the Frequency Domain

Fourier analysis has been an instrumental tool in the development of signal processing. This leads us to wonder whether this framework could similarly benefit generative modelling. In this paper, we explore this question through the scope of time series diffusion models. More specifically, we analyze whether representing time series in the frequency domain is a useful inductive bias for score-based diffusion models. By starting from the canonical SDE formulation of diffusion in the time domain, we show that a dual diffusion process occurs in the frequency domain with an important nuance: Brownian motions are replaced by what we call mirrored Brownian motions, characterized by mirror symmetries among their components. Building on this insight, we show how to adapt the denoising score matching approach to implement diffusion models in the frequency domain. This results in frequency diffusion models, which we compare to canonical time diffusion models. Our empirical evaluation on real-world datasets, covering various domains like healthcare and finance, shows that frequency diffusion models better capture the training distribution than time diffusion models. We explain this observation by showing that time series from these datasets tend to be more localized in the frequency domain than in the time domain, which makes them easier to model in the former case. All our observations point towards impactful synergies between Fourier analysis and diffusion models.

MatterGen: a generative model for inorganic materials design

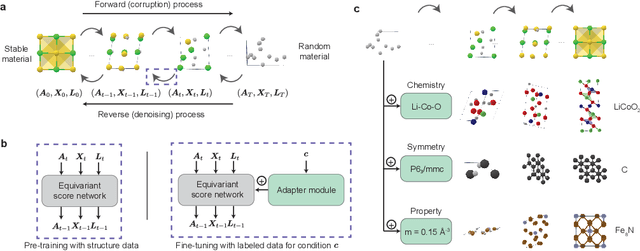
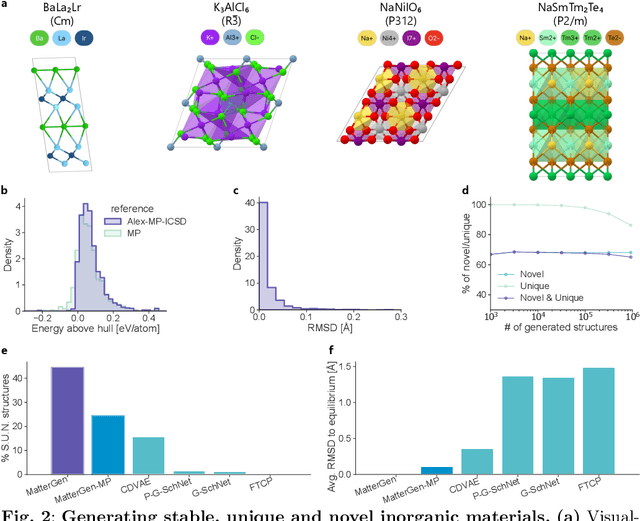
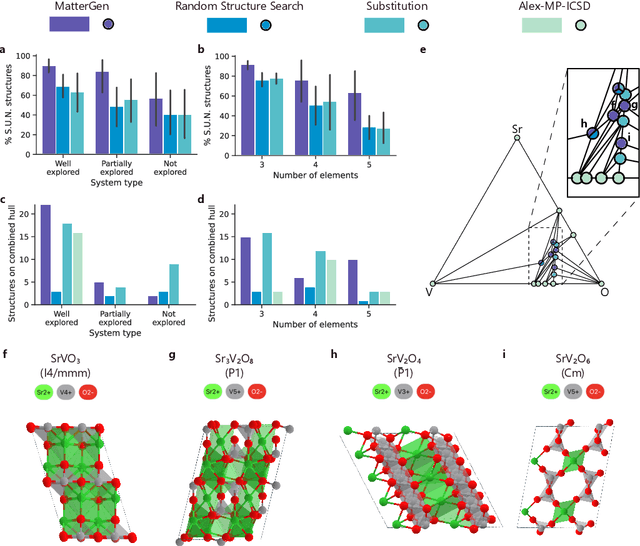
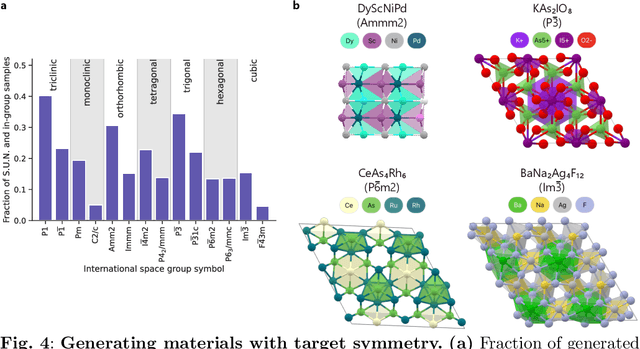
The design of functional materials with desired properties is essential in driving technological advances in areas like energy storage, catalysis, and carbon capture. Generative models provide a new paradigm for materials design by directly generating entirely novel materials given desired property constraints. Despite recent progress, current generative models have low success rate in proposing stable crystals, or can only satisfy a very limited set of property constraints. Here, we present MatterGen, a model that generates stable, diverse inorganic materials across the periodic table and can further be fine-tuned to steer the generation towards a broad range of property constraints. To enable this, we introduce a new diffusion-based generative process that produces crystalline structures by gradually refining atom types, coordinates, and the periodic lattice. We further introduce adapter modules to enable fine-tuning towards any given property constraints with a labeled dataset. Compared to prior generative models, structures produced by MatterGen are more than twice as likely to be novel and stable, and more than 15 times closer to the local energy minimum. After fine-tuning, MatterGen successfully generates stable, novel materials with desired chemistry, symmetry, as well as mechanical, electronic and magnetic properties. Finally, we demonstrate multi-property materials design capabilities by proposing structures that have both high magnetic density and a chemical composition with low supply-chain risk. We believe that the quality of generated materials and the breadth of MatterGen's capabilities represent a major advancement towards creating a universal generative model for materials design.

TRIAGE: Characterizing and auditing training data for improved regression

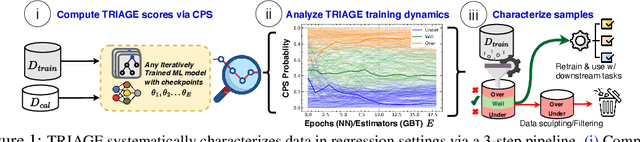
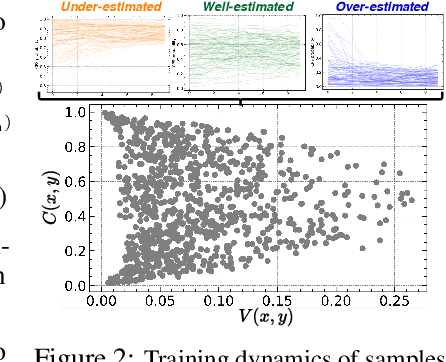
Data quality is crucial for robust machine learning algorithms, with the recent interest in data-centric AI emphasizing the importance of training data characterization. However, current data characterization methods are largely focused on classification settings, with regression settings largely understudied. To address this, we introduce TRIAGE, a novel data characterization framework tailored to regression tasks and compatible with a broad class of regressors. TRIAGE utilizes conformal predictive distributions to provide a model-agnostic scoring method, the TRIAGE score. We operationalize the score to analyze individual samples' training dynamics and characterize samples as under-, over-, or well-estimated by the model. We show that TRIAGE's characterization is consistent and highlight its utility to improve performance via data sculpting/filtering, in multiple regression settings. Additionally, beyond sample level, we show TRIAGE enables new approaches to dataset selection and feature acquisition. Overall, TRIAGE highlights the value unlocked by data characterization in real-world regression applications

Robust multimodal models have outlier features and encode more concepts

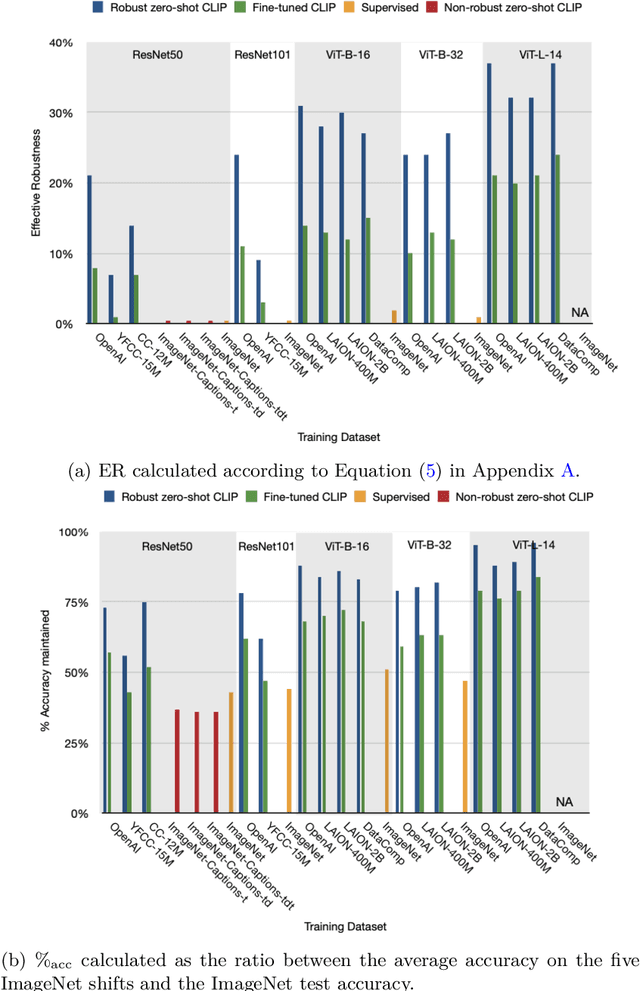
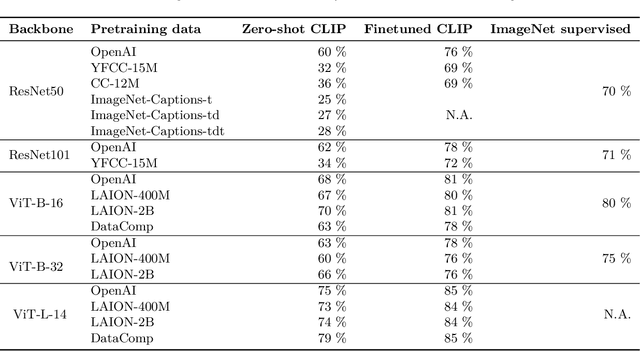
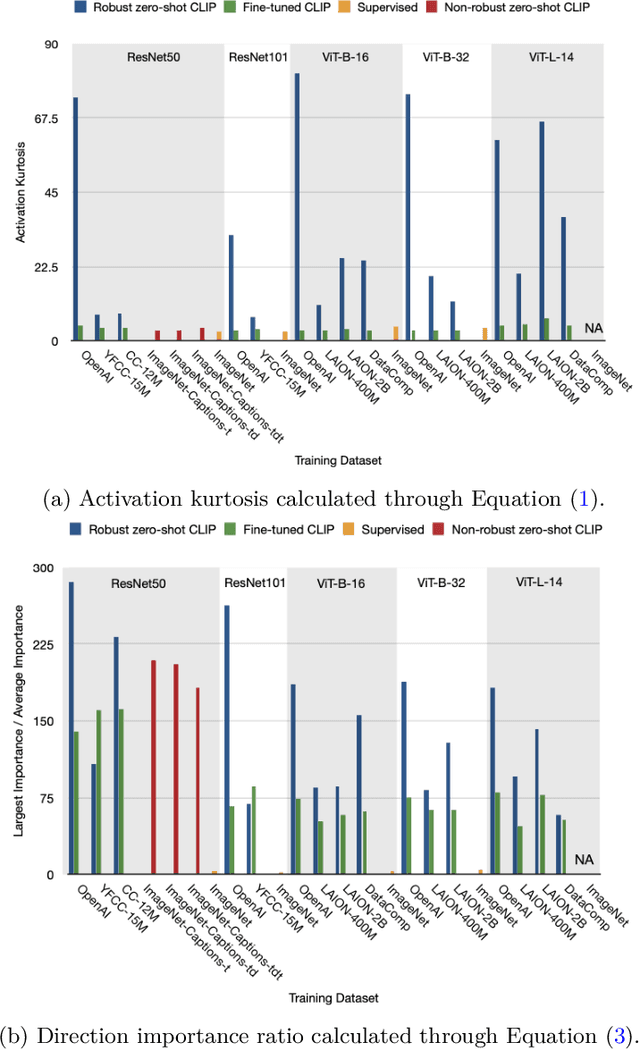
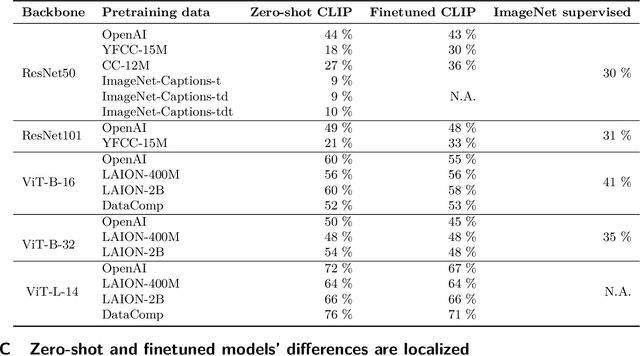
What distinguishes robust models from non-robust ones? This question has gained traction with the appearance of large-scale multimodal models, such as CLIP. These models have demonstrated unprecedented robustness with respect to natural distribution shifts. While it has been shown that such differences in robustness can be traced back to differences in training data, so far it is not known what that translates to in terms of what the model has learned. In this work, we bridge this gap by probing the representation spaces of 12 robust multimodal models with various backbones (ResNets and ViTs) and pretraining sets (OpenAI, LAION-400M, LAION-2B, YFCC15M, CC12M and DataComp). We find two signatures of robustness in the representation spaces of these models: (1) Robust models exhibit outlier features characterized by their activations, with some being several orders of magnitude above average. These outlier features induce privileged directions in the model's representation space. We demonstrate that these privileged directions explain most of the predictive power of the model by pruning up to $80 \%$ of the least important representation space directions without negative impacts on model accuracy and robustness; (2) Robust models encode substantially more concepts in their representation space. While this superposition of concepts allows robust models to store much information, it also results in highly polysemantic features, which makes their interpretation challenging. We discuss how these insights pave the way for future research in various fields, such as model pruning and mechanistic interpretability.

Evaluating the Robustness of Interpretability Methods through Explanation Invariance and Equivariance

Interpretability methods are valuable only if their explanations faithfully describe the explained model. In this work, we consider neural networks whose predictions are invariant under a specific symmetry group. This includes popular architectures, ranging from convolutional to graph neural networks. Any explanation that faithfully explains this type of model needs to be in agreement with this invariance property. We formalize this intuition through the notion of explanation invariance and equivariance by leveraging the formalism from geometric deep learning. Through this rigorous formalism, we derive (1) two metrics to measure the robustness of any interpretability method with respect to the model symmetry group; (2) theoretical robustness guarantees for some popular interpretability methods and (3) a systematic approach to increase the invariance of any interpretability method with respect to a symmetry group. By empirically measuring our metrics for explanations of models associated with various modalities and symmetry groups, we derive a set of 5 guidelines to allow users and developers of interpretability methods to produce robust explanations.

TANGOS: Regularizing Tabular Neural Networks through Gradient Orthogonalization and Specialization

Despite their success with unstructured data, deep neural networks are not yet a panacea for structured tabular data. In the tabular domain, their efficiency crucially relies on various forms of regularization to prevent overfitting and provide strong generalization performance. Existing regularization techniques include broad modelling decisions such as choice of architecture, loss functions, and optimization methods. In this work, we introduce Tabular Neural Gradient Orthogonalization and Specialization (TANGOS), a novel framework for regularization in the tabular setting built on latent unit attributions. The gradient attribution of an activation with respect to a given input feature suggests how the neuron attends to that feature, and is often employed to interpret the predictions of deep networks. In TANGOS, we take a different approach and incorporate neuron attributions directly into training to encourage orthogonalization and specialization of latent attributions in a fully-connected network. Our regularizer encourages neurons to focus on sparse, non-overlapping input features and results in a set of diverse and specialized latent units. In the tabular domain, we demonstrate that our approach can lead to improved out-of-sample generalization performance, outperforming other popular regularization methods. We provide insight into why our regularizer is effective and demonstrate that TANGOS can be applied jointly with existing methods to achieve even greater generalization performance.

Joint Training of Deep Ensembles Fails Due to Learner Collusion

Ensembles of machine learning models have been well established as a powerful method of improving performance over a single model. Traditionally, ensembling algorithms train their base learners independently or sequentially with the goal of optimizing their joint performance. In the case of deep ensembles of neural networks, we are provided with the opportunity to directly optimize the true objective: the joint performance of the ensemble as a whole. Surprisingly, however, directly minimizing the loss of the ensemble appears to rarely be applied in practice. Instead, most previous research trains individual models independently with ensembling performed post hoc. In this work, we show that this is for good reason - joint optimization of ensemble loss results in degenerate behavior. We approach this problem by decomposing the ensemble objective into the strength of the base learners and the diversity between them. We discover that joint optimization results in a phenomenon in which base learners collude to artificially inflate their apparent diversity. This pseudo-diversity fails to generalize beyond the training data, causing a larger generalization gap. We proceed to demonstrate the practical implications of this effect finding that, in some cases, a balance between independent training and joint optimization can improve performance over the former while avoiding the degeneracies of the latter.

Data-IQ: Characterizing subgroups with heterogeneous outcomes in tabular data

High model performance, on average, can hide that models may systematically underperform on subgroups of the data. We consider the tabular setting, which surfaces the unique issue of outcome heterogeneity - this is prevalent in areas such as healthcare, where patients with similar features can have different outcomes, thus making reliable predictions challenging. To tackle this, we propose Data-IQ, a framework to systematically stratify examples into subgroups with respect to their outcomes. We do this by analyzing the behavior of individual examples during training, based on their predictive confidence and, importantly, the aleatoric (data) uncertainty. Capturing the aleatoric uncertainty permits a principled characterization and then subsequent stratification of data examples into three distinct subgroups (Easy, Ambiguous, Hard). We experimentally demonstrate the benefits of Data-IQ on four real-world medical datasets. We show that Data-IQ's characterization of examples is most robust to variation across similarly performant (yet different) models, compared to baselines. Since Data-IQ can be used with any ML model (including neural networks, gradient boosting etc.), this property ensures consistency of data characterization, while allowing flexible model selection. Taking this a step further, we demonstrate that the subgroups enable us to construct new approaches to both feature acquisition and dataset selection. Furthermore, we highlight how the subgroups can inform reliable model usage, noting the significant impact of the Ambiguous subgroup on model generalization.